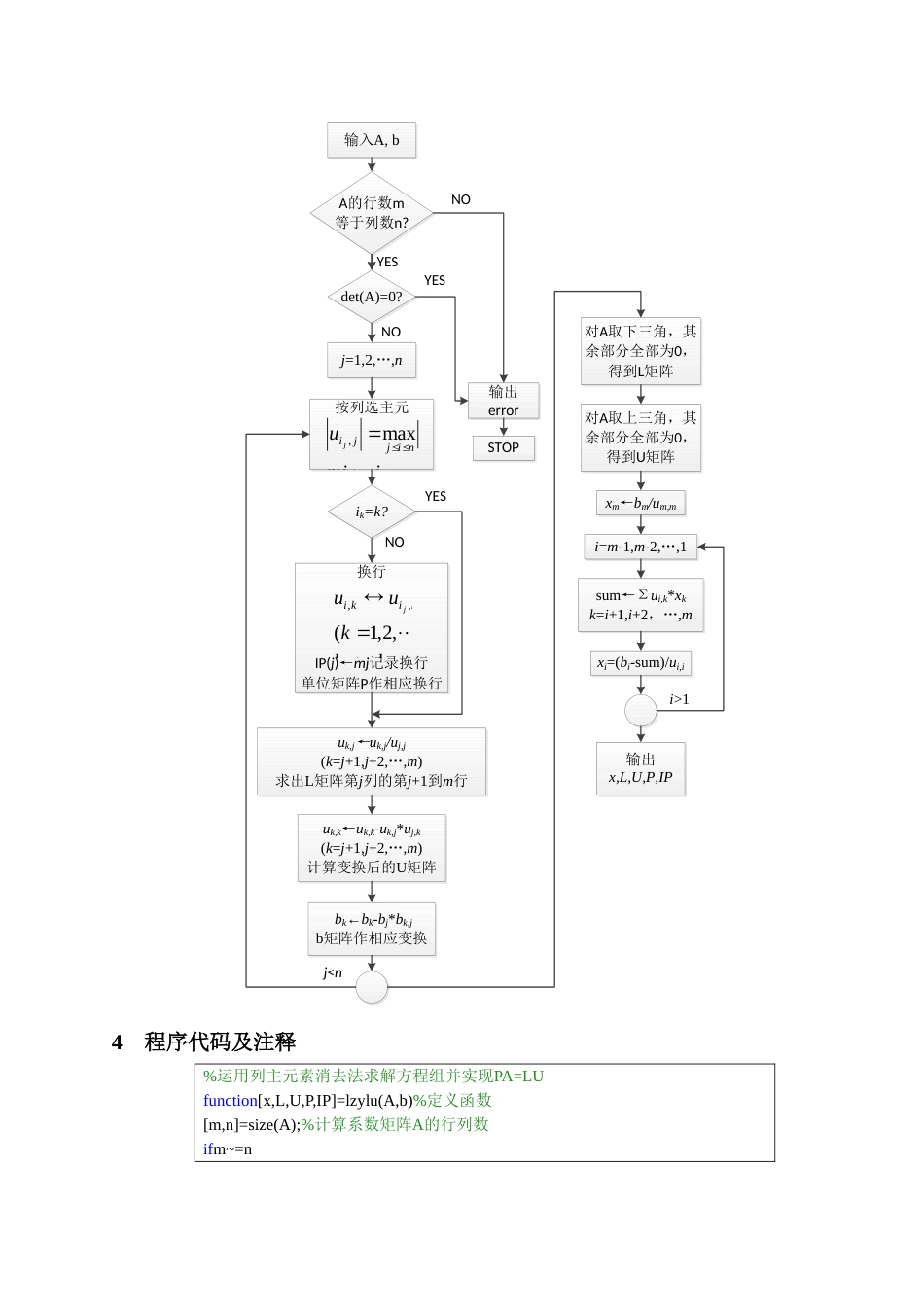
计算方法实验报告实验名称：实验2列主元素消去法解方程组1引言工程实际问题中，线型方程的系数矩阵一般为低阶稠密矩阵和大型稀疏矩阵。用高斯消去法解Ax=b时，可能出现很小，用作除数会导致中间结果矩阵元素数量级严重增长和舍入误差的扩散，使结果不可靠；采用选主元素的三角分解法可以避免此类问题。高斯消去法的消去过程，实质上是将A分解为两个三角矩阵的乘积A=LU，并求解Ly=b的过程。回带过程就是求解上三角方程组Ux=y。所以在实际的运算中，矩阵L和U可以直接计算出，而不需要任何中间步骤，从而在计算过程中将高斯消去法的步骤进行了进一步的简略，大大提高了运算速度，这就是三角分解法。采用选主元的方式与列主元高斯消去法一样，也是为了避免除数过小，从而保证了计算的精确度。2实验目的和要求通过列主元素消去法求解线性方程组，实现PA=LU。要求计算解x，L，U，整形数组IP(i)，(i=1,2,…,)（记录主行信息）。3算法原理与流程图（1）原理将A分解为两个三角矩阵的乘积A=LU。对方程组的增广矩阵经过k-1步分解后，可变成如下形式：第k步分解，为了避免用绝对值很小的数作除数，引进量专业：电气工程及其自动化姓名：李X，于是有=。如果，则将矩阵的第t行与第k行元素互换，将（i,j）位置的新元素仍记为或，然后再做第k步分解，这时（2）流程图输入A,bj=1,2,…,n按列选主元ik=k?imjuuijjinjij,,max输出errorSTOP换行IP(j)←mj记录换行单位矩阵P作相应换行NOjjiikikibbnkuu),2,1(,,uk,j←uk,j/uj,j(k=j+1,j+2,…,m)求出L矩阵第j列的第j+1到m行A的行数m等于列数n?YESNOYESdet(A)=0?NOYESuk,k←uk,k-uk,j*uj,k(k=j+1,j+2,…,m)计算变换后的U矩阵bk←bk-bj*bk,jb矩阵作相应变换对A取下三角，其余部分全部为0，得到L矩阵对A取上三角，其余部分全部为0，得到U矩阵j<ni=m-1,m-2,…,1xm←bm/um,msum←Σui,k*xkk=i+1,i+2，…,mxi=(bi-sum)/ui,ii>1输出x,L,U,P,IP4程序代码及注释%运用列主元素消去法求解方程组并实现PA=LUfunction[x,L,U,P,IP]=lzylu(A,b)%定义函数[m,n]=size(A);%计算系数矩阵A的行列数ifm~=nerror('系数矩阵不是方阵');return;endifdet(A)==0%计算矩阵A的行列式，若为零则A是奇异矩阵error('矩阵不能被三角形分解')endu=A;v=b;q=eye(m);s=q;%定义单位矩阵forj=1:m-1%按照列循环t=abs(u(j,j));mj=j;fori=j:mifabs(u(i,j))>tmj=i;endend%比较大小，选列主元素ifu(mj,j)==0error('系数矩阵奇异');returnendB=u(j,:);c=v(j);u(j,:)=u(mj,,:);v(j)=v(mj);u(mj,:)=B;v(mj)=c;%交换两行，将列主元素所在行移到第j行IP(j)=mj;%记录互换，表示第j行与第IP(j)行互换ts=s(j,:);s(j,:)=s(mj,:);s(mj,:)=ts;%置换矩阵进行相应行交换u(j+1:m,j)=u(j+1:m,j)/u(j,j);%求出L矩阵第j列第j+1到第m行元素u(j+1:m,j+1:m)=u(j+1:m,j+1:m)-u(j+1:m,j)*u(j,j+1:m);%解出u矩阵做完第j次消元后的矩阵v(j+1:m)=v(j+1:m)-v(j)*u(j+1:m,j);%v也要对应系数进行运算，相比杜利特尔（Doolittle）分解法减少了l*y=b，y=u*x先要求解y再求x的过程endP=s;L=tril(u,-1)+q;%对u取下三角，其余部分全部为0，得到L矩阵U=triu(u);%对u取上三角，其余部分全部为0，得到U矩阵x(m)=v(m)/u(m,m);fori=m-1:-1:1sum=0;fork=i+1:msum=sum+U(i,k)*x(k);endx(i)=(v(i)-sum)/u(i,i);end%利用U*x=v，求解x得到行向量x=x';%转置为列向量5算例分析解方程组>>A=[1111111;2111111;3211111;4321111;5432111;6543211;7654321];>>b=[781013172228]';>>[x,L,U,P,IP]=lzylu(A,b)x=L=1.00000000000.28571.0000000000.42860.80001.000000000.57140.60000.75001.00000000.71430.40000.50000.66671.0000000.1429-0.2000-0.2500-0.3333-0.50001.000000.85710.20000.25000.33330.5000-1.00000.0000U=000000.50000.00000000000.0000P=0000001010000000100000001000000010010000000000010IP=723457本程序将方程组系数矩阵进行列主元素三角形分解，得到矩阵L,U,P和记录主行变换的数组IP(i)。6讨论与结论（1）程序lzylu.m具有以下特点：1.当系数矩阵是奇异矩阵时输出提示错误信息，停止运算2.当系数矩阵不是方阵时，提示错误...