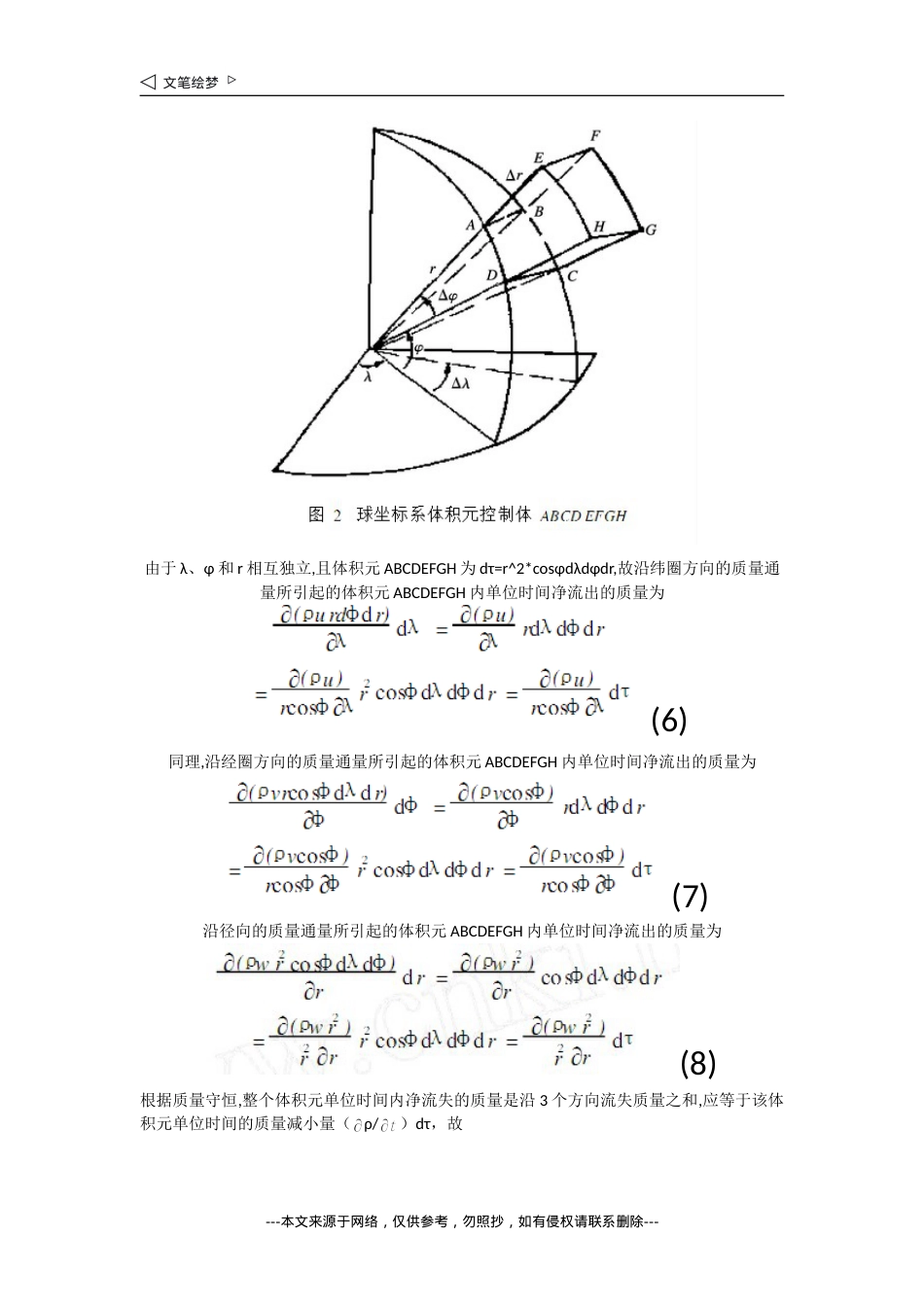
《流体力学》连续方程推导的巧方法施春华,高庆九,李忠贤(南京信息工程大学大气科学学院,江苏南京210044)摘要:针对柱坐标系和球坐标系下《流体力学》中连续方程形式复杂、理解不便的特点,采用欧拉控制体方法,把“质量通量”整体作为一物理量,从而巧妙地推导了这两类连续方程,该过程物理意义明确、数学算法简单,有助于学生理解。关键词:连续方程;柱坐标系;球坐标系在大学《流体力学》教学中,连续方程是最基本的内容之一,在很多相关专业课程中得到广泛应用。相对而言,在直角坐标系中的连续方程形式简单,也易于理解,但在柱坐标系和球坐标系中,连续方程的形式却相对复杂,理解相对困难。目前,很多参考书[123]对于后两类连续方程要么没有给出具体推导,要么推导过程较为复杂,使数理基础较薄弱的学生难以理解,在此,笔者结合教学中的实际经验,演示柱坐标系和球坐标系下一种物理意义明确、数学理解简单的连续方程的推导过程。1连续方程的一般算子形式流体运动的连续方程,是表示流体运动和其质量分布的关系式。在拉格朗日方法中,某流体块在运动时其体积和形状尽管可发生变化,但它始终由这些流点构成,因此它的质量不变。由此可见,连续方程实质上是质量守恒定律在“连续介质”(流体)中的应用。一般的拉格朗日方法考虑,某个别流体微团(质量体)在运动过程中,其随体密度的变化,必然与其体积变化趋势相反,如体积膨胀,它的密度减小,体积收缩,则密度增大。其算子形式的通用表达式[1](1)一般的欧拉方法考虑,对于某固定位置的空间单位体积元(控制体)来说,该体积元内单位时间的质量变化,与该体积元边界上的质量通量变化相联系,如质量往外流,它的密度减小,反之则增大。其算子形式的通用表达式[1](2)两种方法的区别:拉格朗日方法多从物理量的定义出发,模型简单容易理解,但数学解析在实际应用中有些困难;欧拉方法则通过适当的数学建模后,能在数学上给出方便的解析,有利于从数学角度更好地理解概念。在直角坐标系中,通过建立三维空间微元控制体(图略,很多教科书都详细给出,且易于理解),很容易得到(2)式在三维直角坐标系下连续性微分方程的一般表达式(3)---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---2柱坐标系欧拉连续方程基于柱坐标系把“质量通量”整体作为一物理量的考虑,物理意义明确,数学理解简单的欧拉连续方程的推导见图1。如图1所示,柱坐标系体积元控制体ABCDEFGH,径向方向r,圆周切向方向θ,垂直方向z,径向速度Vr,圆周切向速度Vθ,垂直速度w,则径向线微元AB表达为dr,切向线微元AD表达为rdθ,垂直微元GC为dz,体积微元dV=rdθdrdz。由径向速度Vr垂直穿越面元ADHE和BCGF(面积rdθdz)所引起的质量通量均可表达为ρVr*rdθdz,但r坐标值在两个面元处有差异。这使得质量通量沿径向r方向不尽相同就表达了质量通量在穿越面元ADHE和BCGF时沿径向r方向的梯度,乘以dr后得它表示了径向速度Vr垂直穿越面元ADHE和BCGF后导致体积元ABCDEF2GH内质量通量的变化量(略去高阶小量,下同),即径向速度Vr引起的体积元ABCDEFGH内单位时间净流出的质量。同理,由切向速度Vθ垂直穿越面元DCGH和ABFE(面积rdθdr)所引起的质量通量均可表达为ρVθdrdz,但θ坐标值在两面元处不同,质量通量沿切向θ方向的梯度描述为(ρVθdrdz)/,而（(ρVθdrdz)/）dθ则描述了切向速度Vθ垂直穿越面元DCGH和ABFE后导致体积元ABCDEF2GH内质量通量的变化量,即切向速度Vθ引起的体积元ABCDEFGH内单位时间净流出的质量。同理,垂直速度w垂直穿越面元EFGH和ABCD(面积rdθdr)所引起的质量通量均可表达为ρwrdθdr,但z坐标值在两面元处不同,质量通量沿z方向的梯度描述为(ρwrdθdr)/z,而（(ρwrdθdr)/z）dz则描述了垂直速度w垂直穿越面元EFGH和ABCD后导致体积元ABCDEFGH内质量通量的变化量,即垂直速度w引起的体积元ABCDEFGH内单位时间净流出的质量。该柱坐标中,流体所有运动可以分解为在3个正交的方向r、θ和z上运动,所以流体单位---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---时间净流出控制体ABCDEFGH的质量就表达为,式中r、θ和z相互独立,密度ρ则是空间的函数,体积微元dV=rdθdrdz,故有(...