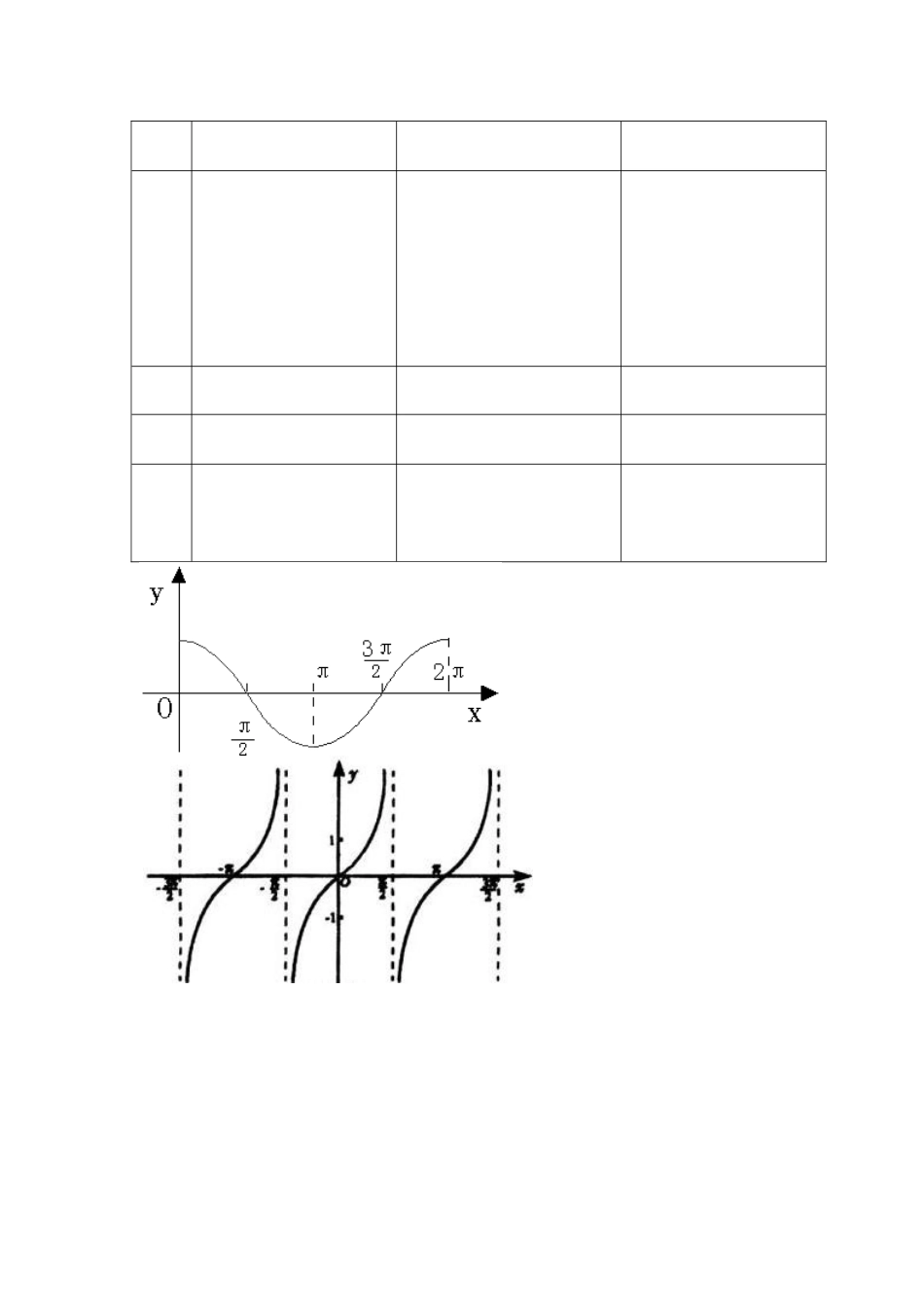
三角函数知识点总结按逆时针方向旋转形成的角正角:按顺时针方向旋转形成的角负角:1、任意角不作任何旋转形成的角零角:x的顶点与原点重合，角的始边与为第几象限角．2、角轴的非负半轴重合，终边落在第几象限，则称k36090k360,k第一象限角的集合为,k360k36090k180第二象限角的集合为360k180k360270,k第三象限角的集合为k360,k360360k270第四象限角的集合为x,kk180终边在轴上的角的集合为18090,kky终边在轴上的角的集合为90,kk终边在坐标轴上的角的集合为k,k360、与角终边相同的角的集合为3*xnn轴的正半轴的上方起，等份，所在象限的方法：先把各象限均分4、已知再从是第几象限角，确定n依次将各区域标上一、二、三、四，则终边所落在的区域．原来是第几象限对应的标号即为n15、长度等于半径长的弧所对的圆心角叫做弧度．lrl的弧度数的绝对值是所对弧的长为、半径为，则角的圆的圆心角6．r1801360257.317、弧度制与角度制的换算公式：．，，180rl为弧度制rC2rCSll，，8、若扇形的圆心角为，面积为，半径为，弧长为，则，周长为112rSlr．2222yx,0yrxr，的坐标是，它与原点的距离是是一个任意大小的角，的终边上任意一点9、设yxy0tanxsincos．，，则rrx10、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正．tancossin．，，11、三角函数线：y221sincos1、同角三角函数的基本关系：12TPMxOA-1-sin2222tan2sin,coscos1sin1；cossincossintan,cos．tan13、三角函数的诱导公式：2ktank1sin2kcosktansincos2．，，tancoscossin2tansin．，，tansintancos3sincos．，，tan4sincossincostan．，，口诀：函数名称不变，符号看象限．{符号看象限，就是把α看作是某一个锐角（例如30°、45°、60°之类），然后π+α、π-α、-α就看作是π与这个锐角相加减或者相反后的角，然后根据这个角在第几象限，来判断三角函数的正负。例如把α看作是30°，所以π+α为210°第三象限角，所以sin为负、cos为负、tan为正，也就是诱导公式二了。结论：当把把α看作是某一个锐角时，π+α、π-α、-α就分别为第三、第二、第四象限角了，又例如：sin（3π+α）先化成sin【2π+（π+α）】，再化成sin（π+α），因为π+α第三象限角，而第三象限角的sin为负，所以sin（π+α）=-sinα，}=-sinα+α））π+α】=sin（π【sin用等式表示为（3π+α）=sin2π+（sin5sin6sincoscoscoscossin．，．，2222口诀：正弦与余弦互换，符号看象限．（这里的符号看象限，跟上面的一样道理，不同的是π减小到一半而已，其他没变，同样把α看作是某一个锐角，然后来判断）-2-三角函数的图象与性质※※※知识点归纳一、三角函数的图象与性质1、正弦函数、余弦函数和正切函数的图象与性质：函数性质xsinyycosxytanx图象,xxkkRR定义域2,111,1R值域x2kk2xkk当时，当21y1y2kx时，；当；maxmax最值既无最大值也无最小值k1yxk2k．时，当min21y．时，min22周期性偶函数奇函数奇偶性奇函数2kk,2k上在k,2k2在,kk22在单调性22是增函数；-3-k上是增...