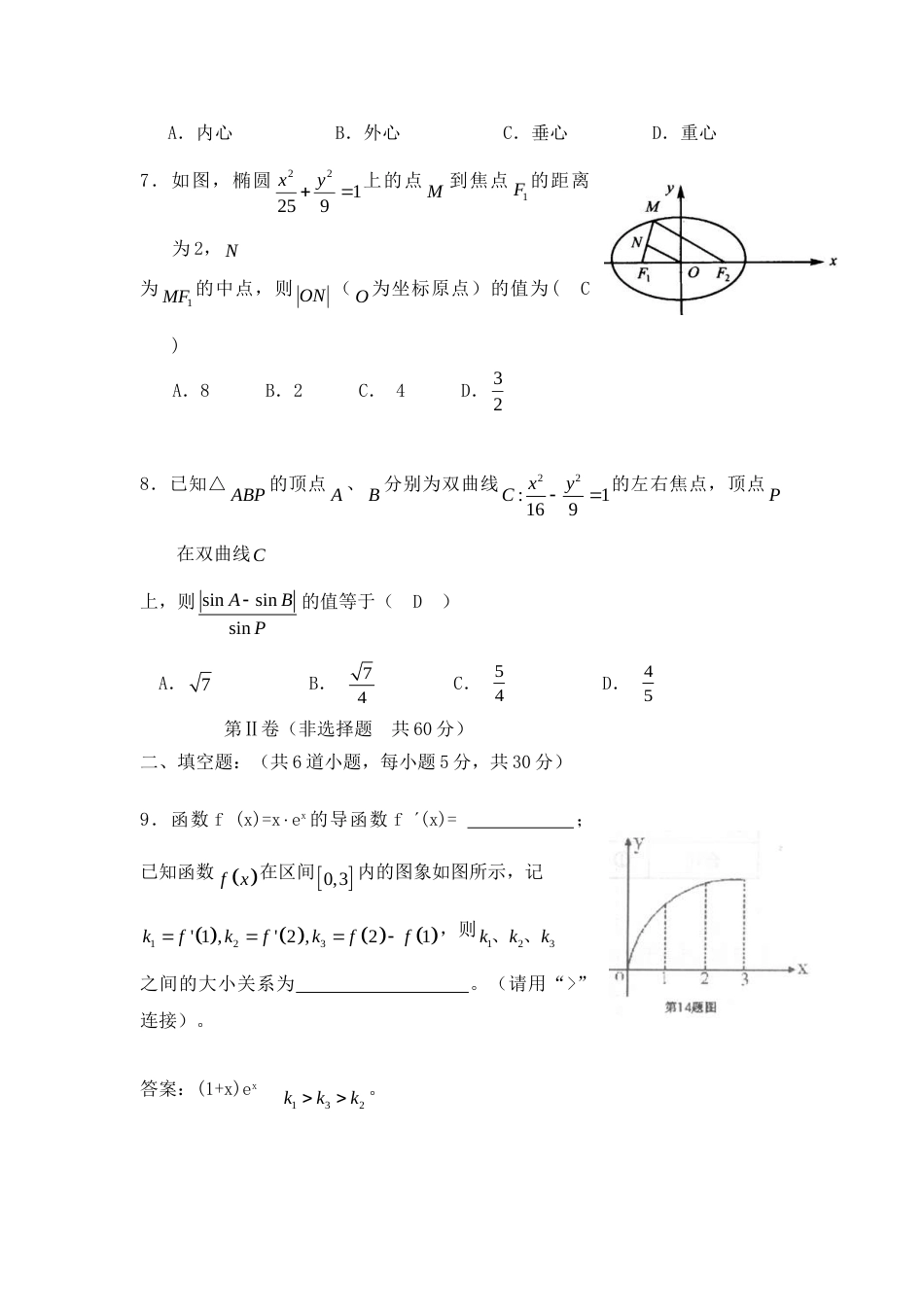
ACPB北京市第十八中学2020学年第一学期高二数学期末模拟考试数学(理)试卷第Ⅰ卷(选择题共40分)一、选择题:(共8道小题,每小题5分,共40分,选对一项得5分,多选则该小题不得分。)1.下列曲线中离心率为62的是(C)A.22124xyB.22146xyC.22142xyD.221410xy2.下列有关命题的说法中错误的是(D)A.若pq为假命题,则p、q均为假命题.B.“1x”是“2320xx”的充分不必要条件.C.命题“若2320,xx则1x”的逆否命题为:“若1,x则2320xx”.D.对于命题p:xR使得21xx<0,则p:xR,使210xx.3.如图,在Rt△ABC中,∠ABC=900,PA⊥平面ABC,则四面体P-ABC中共有(A)个直角三角形A.4B.3C.2D.14.曲线21xyx在点1,1处的切线方程为(B)A.xy2=0B.x+y2=0C.x+4y5=0D.x4y5=05.ABC中,(2,0)A、B(2,0)、C(3,3),则AB边的中线对应方程为(B)A.xyB.3)xx(0yC.xyD.3)xx(0y6.已知P为△ABC所在平面α外一点,侧面与底面所成的二面角相等,则P点在平面α内的射影一定是△ABC的(A)A.内心B.外心C.垂心D.重心7.如图,椭圆192522xy上的点M到焦点1F的距离为2,N为1MF的中点,则ON(O为坐标原点)的值为(C)A.8B.2C.4D.238.已知△ABP的顶点A、B分别为双曲线22:1169xyC的左右焦点,顶点P在双曲线C上,则sinsinsinABP的值等于(D)A.7B.74C.54D.45第Ⅱ卷(非选择题共60分)二、填空题:(共6道小题,每小题5分,共30分)9.函数f(x)=xex的导函数f(x)=;已知函数fx在区间0,3内的图象如图所示,记123'1,'2,21kfkfkff,则123kkk、、之间的大小关系为。(请用“>”连接)。答案:(1+x)ex132kkk。10.已知6),6,(3a,)2,3,1(b为两平行平面的法向量,则。答案:21。11.直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且DAB=60的菱形,,ACBDO11111ACBDO,则二面角O1BCD的大小为。答案:60。12.命题“xR,使2230axax成立”是假命题,则实数a的取值范围为。答案:[0,3]。13.以正方形ABCD的相对顶点A、C为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为;设1F和2F为双曲线22221xyab(0,0ab)的两个焦点,若12F,F,P(0,2)b是正三角形的三个顶点,则双曲线的离心率为;经过抛物线24y1x的焦点作直线交抛物线于),),(,(2211yBxyAx两点,若521yy,则线段AB的长等于__________.答案:1022;2;7。14.已知命题p:存在xR,使tan1x,命题q:2320xx的解集是{|12}xx,下列结论:①命题“p且q”是真命题;②命题“p且¬q”是假命题;③命题“¬p或q”是真命题;④命题“¬p或¬q”是假命题,其中正确的有.答案:①②③④。三、解答题:(共4道小题,6+9+8+7分)15.已知函数2ln()bxxafx图象上一点P(2,f(2))处的切线方程为22ln23xy,求a,b的值。解:babfabxfxaxf4ln2(2)4,2('2),2)(',22ln26(2)f所以22ln2642ln342baba,解得1,2ba。16.如图四棱锥PABCD的底面是正方形,PD底面ABCD,点E在棱PB上,O为AC与BD的交点。(1)求证:平面AEC平面PDB;(2)当E为PB中点时,求证:OE//平面PDA,OE//平面PDC。(3)当2PDAB且E为PB的中点时,求AE与平面PBC所成的角的大小。证明:(1) 四边形ABCD是正方形,∴AC⊥BD, PD底面ABCD,∴PD⊥AC,DPDBD∴AC⊥平面PDB,又AC平面AEC∴平面AEC平面PDB.(2) 四边形ABCD是正方形,OBOD,在PBD中,又PEBEOE//PD,又PADPDPADOE平面,平面OE//平面PDA,同理可证OE//平面PDC。解:(3) PD底面ABCD,DCPDDAPD,,又DADC所以,可以D为坐标原点建立如图的空间直角坐标系D-xyz。设AB=1.则D(0,0,0),A(1,0,0),C(0,1,0),B(1,1,0),P(0,0,2),)(,,222121E从而,),,(22212-1AE,),(,100CB,(,,)20-1PC设平面PBC的一个法向量为(,,)zyxn。由...