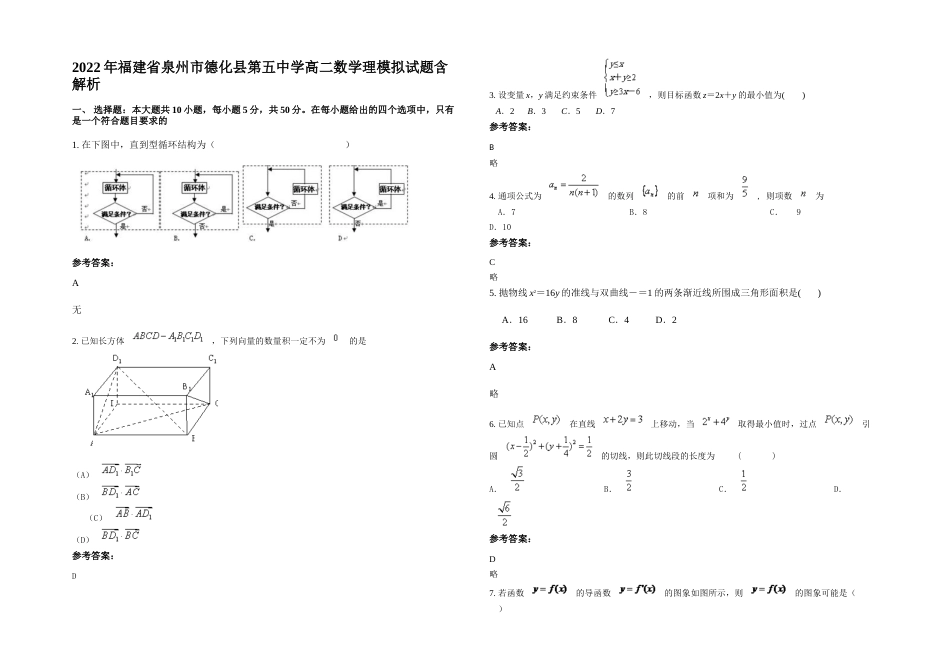
2022年福建省泉州市德化县第五中学高二数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.在下图中，直到型循环结构为（）参考答案：A无2.已知长方体，下列向量的数量积一定不为的是（A）（B）（C）（D）参考答案：D3.设变量x，y满足约束条件，则目标函数z＝2x＋y的最小值为()A．2B．3C．5D．7参考答案：B略4.通项公式为的数列的前项和为,则项数为A．7B．8C．9D．10参考答案：C略5.抛物线x2＝16y的准线与双曲线－＝1的两条渐近线所围成三角形面积是()A．16B．8C．4D．2参考答案：A略6.已知点在直线上移动，当取得最小值时，过点引圆的切线，则此切线段的长度为()A．B．C．D．参考答案：D略7.若函数的导函数的图象如图所示，则的图象可能是（）A.B.C.D.参考答案：C【分析】通过对比导函数图像和原函数图像，导函数为负，原函数递减，导函数为正，原函数为增，于是可得答案.【详解】从导函数图像可看出，导函数先负再正再负，于是原函数先减再增再减，排除AD，再对比，函数极小值点为正，故答案为C.【点睛】本题主要考查导函数图像与原函数之间的关系，意在考查学生的图像识别能力，分析能力，难度不大.8.设集合,,,则集合C中元素的个数为()A.11B.9C.6D.4参考答案：A【分析】由题意可得出：从,,任选一个；或者从,任选一个；结合题中条件,确定对应的选法，即可得出结果．【详解】解：根据条件得：从,,任选一个,从而,,任选一个,有种选法；或时,,有两种选法；共种选法；C中元素有个．故选：A．【点睛】本题主要考查列举法求集合中元素个数，熟记概念即可，属于基础题型.9.定义方程f（x）=f′（x）的实数根x0叫做函数f（x）的“新驻点”，若函数g（x）=x，h（x）=ln（x+1），φ（x）=x3﹣1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为（）A．α＞β＞γB．β＞α＞γC．γ＞α＞βD．β＞γ＞α参考答案：C【考点】63：导数的运算．【分析】分别对g（x），h（x），φ（x）求导，令g′（x）=g（x），h′（x）=h（x），φ′（x）=φ（x），则它们的根分别为α，β，γ，即α=1，ln（β+1）=，γ3﹣1=3γ2，然后分别讨论β、γ的取值范围即可．【解答】解： g′（x）=1，h′（x）=，φ′（x）=3x2，由题意得：α=1，ln（β+1）=，γ3﹣1=3γ2，① ln（β+1）=，∴（β+1）β+1=e，当β≥1时，β+1≥2，∴β+1≤＜2，∴β＜1，这与β≥1矛盾，∴﹣1＜β＜1；② γ3﹣1=3γ2，且γ=0时等式不成立，∴3γ2＞0∴γ3＞1，∴γ＞1．∴γ＞α＞β．故选C．10.下列命题中，a、b、c表示不同的直线，表示不同的平面，其真命题有（）①若，则②若，则③a是的斜线，b是a在上的射影，，，则④若则A.1个B.2个C.3个D.4个参考答案：B略二、填空题:本大题共7小题,每小题4分,共28分11.14．若双曲线的渐近线与方程为的圆相切，则此双曲线的离心率为．参考答案：212.在极坐标系中，圆上的点到直线的距离的最小值是.参考答案：113.某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮练习，每人投10次，投中的次数如下表：学生1号2号3号4号5号甲班67787乙班67679则以上两组数据的方差中较小的一个为=.参考答案：14.设圆C：（x﹣3）2+（y﹣5）2=5，过圆心C作直线l交圆于A，B两点，与y轴交于点P，若A恰好为线段BP的中点，则直线l的方程为．参考答案：y=2x﹣1或y=﹣2x+11【考点】直线与圆相交的性质；直线的一般式方程．【分析】由题意可设直线L的方程为y﹣5=k（x﹣3），P（0，5﹣3k），设A（x1，y1），B（x2，y2），联立，然后由方程的根与系数关系可得，x1+x2，x1x2，由A为PB的中点可得x2=2x1，联立可求x1，x2，进而可求k，即可求解直线方程【解答】解：由题意可得，C（3，5），直线L的斜率存在可设直线L的方程为y﹣5=k（x﹣3）令x=0可得y=5﹣3k即P（0，5﹣3k），设A（x1，y1），B（x2，y2）联立消去y可得（1+k2）x2﹣6（1+k2）x+9k2+4=0由方程的根与系数关系可得，x1+x2=6，x1x2=① A为PB的中点∴即x2=2x1②把②代入①可得x2=4，x1=2，x1x2==8∴k=±2∴直线l的方程为y﹣5=±2（x﹣3）即y=2x﹣1或y=﹣2x+11故答案...