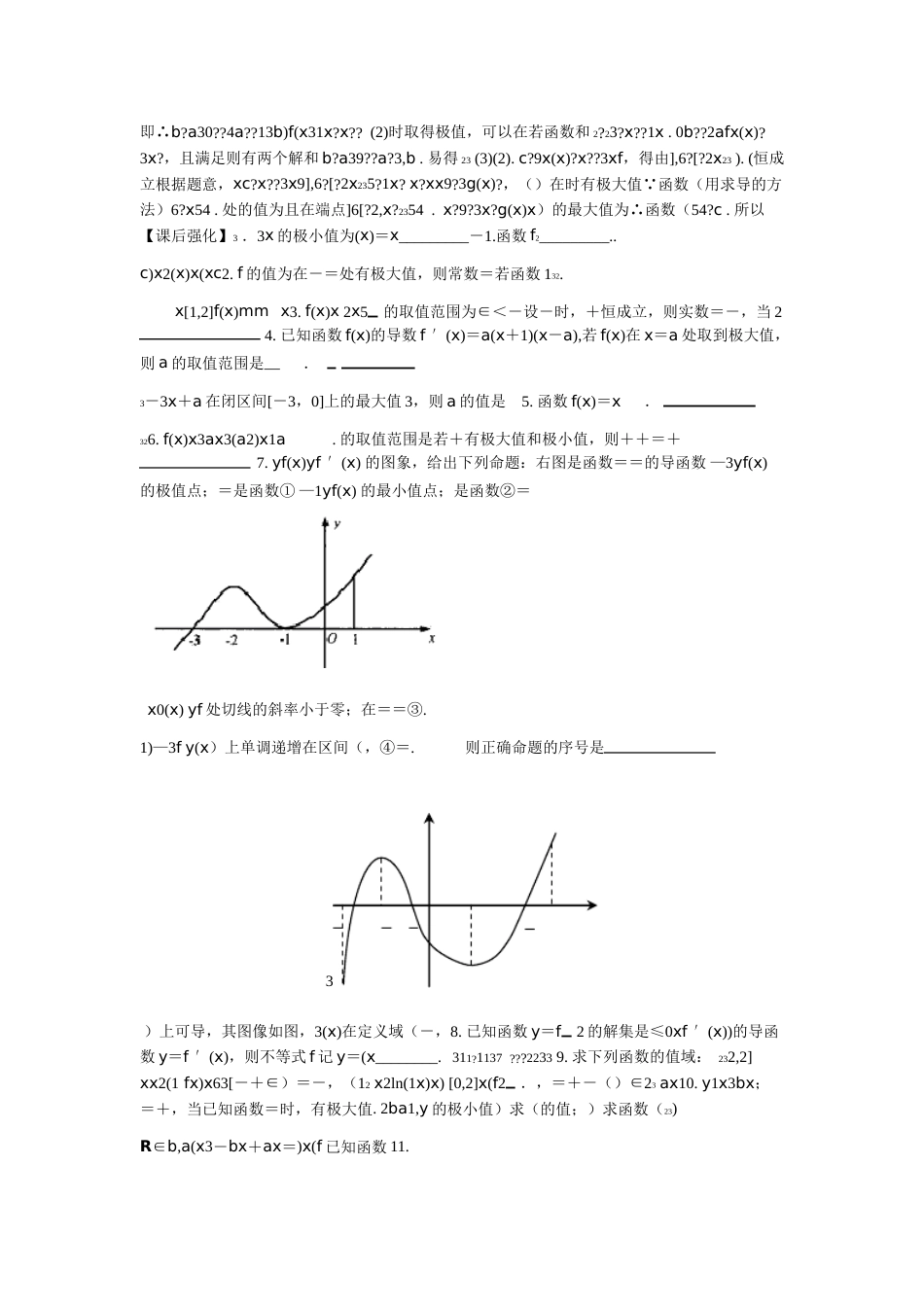
——0216极值和最值课时第导数在函数中的应用【基础再现】43_________xxxx1.f(x)4x．－＝已知函数处取极值，则＝在＝003答案：意图：求函数的极值点xln.2.y的极大值点为函数＝x''x??xln(lnx)1x?lnxex?x?e'''0?y?0ye???0,xy?时，答案：令时，；当，当，22xx1?e)y?f(x=e.，在定义域内只有一个极值点为极大值e意图：求函数的极大值点4.3.yx4x3[2,3]上的最小值为－在区间函数＝－＋'3'3''0?时,y?当x1时,y?0;当x?14,y?4x?令y?0,4x?4?0,x?1,答案：0,??y|y072y??y|27,y|?，得得而端点的函数值1?x极小值min3x???x2.意图：复习求最值的基本方法π.]4.yx2cosx[0,上的最大值是＋＝在区间函数2??3答案：6.意图：考察有关三角函数极值和最值的问题32bx30x1x3a2b5.yxax．＋处有极值，则在若函数＝－＝＝和＋＋＋＝15答案：－意图：已知极值求变量的值【典型例题】13132＋1在区间[－3,)＝xx]上的极值和最值．例1．求函数f(x－3225答案：极大值f(0)＝1，极小值f(1)＝6最大值1，最小值f(－3)＝－12.5意图：复习列表求函数的极值和最值223________.abbxax110x2f(x)ax的值分别为＋时有极值在＝例＋．函数，＋＝，那么'2'2114,?0,f(?1)a?a?b?3x?2ax??2a?b?3110?,?bf(1)?f(x)解：2a?b??3a??3a?4???,,或a??3x?1???不是极值点，当时，2b?3b??11a?a?b?9???“0”“”.的必要条件，故需检验所求的结果导数等于意图：知道极值求参数，应注意，此点为极值点只是43－bx＋4，当x＝2ax)(．若函数例3fx＝时，函数f(x)有极值－，3．（1）求函数的解析式；（2）若函数f(x)＝k有3个解，求实数k的取值范围．??2?bax?f?3x,解：???1?12a?fb?20?????a4解得）由题意：1.,（??3???8a?22b?4?f???b?43??1??3x?4xx??f4?所求解析式为3??????2?2??xxf?2x??x4）可得：（2）由（1???x?2x??20?fx令，得或?????xxffx的变化情况如下表：、变化时，当xy????,?22???,2?22????2,???xf?0—0???xf单调递增↗283单调递减↘4?3单调递增↗28??2?x?xf有极大值时，因此，当3;4??2x?xf?;当时，有极小值3281??334?4fxx??x?y=k的图象大致如图：函数3284?k??由图可知：3302?2x4?31）极大值，极小值是否就是最大值，最小值，要与区间两端点的函数值进行比较，才能下结设计意图：（f'(x)?0(或f'(x)?0)f(x)2.恒成立，）在已知函数论（是增函数（或减函数）求参数的取值范围时，应令f'(x)00，则参数的这个值应舍去，恒等于解出参数的取值范围，然后检验参数的取值能否使，若能恒等于?(a,b)0)0(?或f'(x)?'(fx).0f'(x)x恒成立解出的参数的取值范围确定，若不恒为，则由23＋bx＋c的图象为曲线x(fx)＝E－ax.变式：已知函数()EPEPxa,b的关系；轴平行，求点处的切线与在，使曲线上存在点若曲线Ⅰ．()f(x)x1x3a,b的值；说明函数和时取得极值，并求此时＝－＝Ⅱ可以在()()f(x)2cx[2,6]c.的取值范围Ⅱ的条件下，在－Ⅲ∈在满足恒成立，求＜2P(x,y)y?f(x)?b?x?2x)?3xfa(P,(1),的切线的斜率在点则曲线设切点为解：0022??0?b?3x?2?2ax?bfax(x)?k?f?(x)3x,有解，由题意知00000022.即∴b?a30??4a??13b)f(x31x?x??(2)时取得极值，可以在若函数和2?23?x??1x.0b??2afx(x)?3x?，且满足则有两个解和b?a39??a?3,b.易得23(3)(2).c?9x(x)?x??3xf，得由],6?[?2x23).(恒成立根据题意，xc?x??3x9],6?[?2x235?1x?x?xx9?3g(x)?，（）在时有极大值 函数（用求导的方法）6?x54.处的值为且在端点]6[?2,x?2354.x?9?3x?g(x)x）的最大值为∴函数（54?c.所以【课后强化】3．3x的极小值为(x)＝x_________－1.函数f2_________..c)x2(x)x(xc2.f的值为在－＝处有极大值，则常数＝若函数132.x[1,2]f(x)mmx3.f(x)x2x5的取值范围为∈＜－设－时，＋恒成立，则实数＝－，当24.已知函数f(x)的导数f′(x)＝a(x＋1)(x－a),若f(x)在x＝a处取到极大值，则a的取值范围是__．3－3x＋a在闭区间[－3，0]上的最大值3，则a的值是5.函数f(x)＝x．326.f(x)x3ax3(a2)x1a.的取值范围是若＋有极大值和极小值，则＋＋＝＋7.yf(x)yf′(x)的图象，给出下列命题：右图是函数＝＝的导函数—3yf(x)的极值点；＝是函数①—1yf(x)的最小值点；是函数②＝x0(x)yf处切线的斜率小于零；在＝＝③.1)—3fy(x）上单调递增在区间（，...