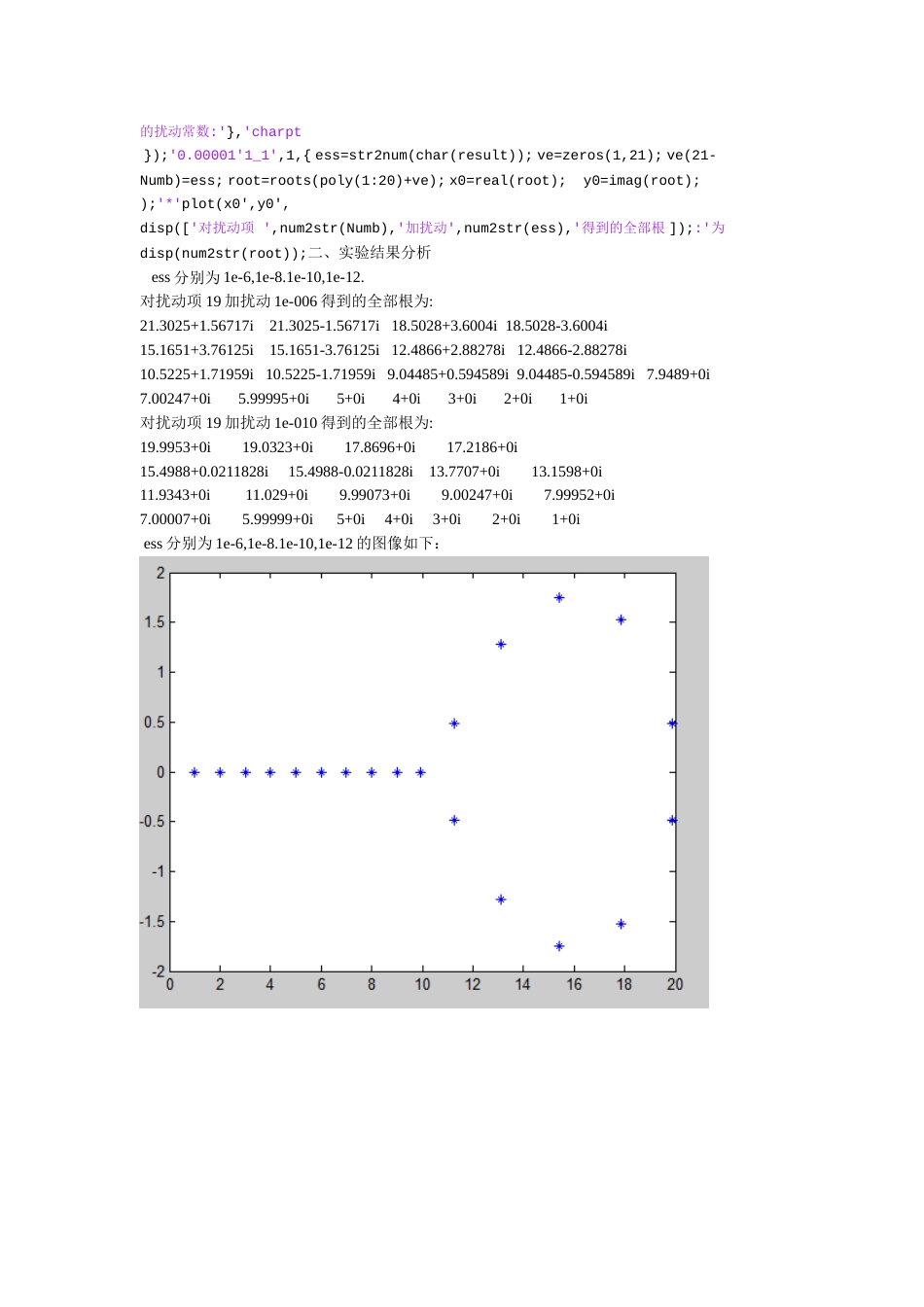
数值计算方法上机题目11、实验1.病态问题实验目的：算法有“优”与“劣”之分，问题也有“好”和“坏”之别。所谓坏问题就是问题本身的解对数据变化的比较敏感，反之属于好问题。希望读者通过本实验对此有一个初步的体会。数值分析的大部分研究课题中，如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决，当然一般要付出一些代价（如耗用更多的机器时间、占用更多的存储空间等）。问题提出：考虑一个高次的代数多项式20?)kx20)??(?1)(x?2)...(x?)p(x?(x）E1-1（1?k显然该多项式的全部根为l，2，…，20，共计20个，且每个根都是单重的（也称为简单的）。现考虑该多项式方程的一个扰动19??x)?0xp((E1-2)19?x的系数作一个小的扰动。我们希望是一个非常小的数。这相当于是对（E1-1其中）中）的解对扰动的敏感性。E1-2）根的差别，从而分析方程（E1-1比较（E1-1）和（：实验内容”，输入函数roots”和“poly为了实现方便，我们先介绍两个Matlab函数：“）（au＝rootsnua1?n的元素依次a维的向量，则该函数的输出其中若变量维的向量。设存储为一个a,...,,aau，则输出为的各分量是多项式方程1?2n1nn?1?...axx??axa?0a1n12n?的全部根，而函数b=poly(v)的输出b是一个n＋1维变量，它是以n维变量v的各分量为根的多项式的系数。可见“roots”和“Poly”是两个互逆的运算函数.ve=zeros(1,21);ve(2)=ess;roots(poly(1:20))+ve)?。中的）ess”即是（E1-2程序中的（上述简单的Matlab程序便得到E1-2）的全部根，“实验要求：（1）选择充分小的ess，反复进行上述实验，记录结果的变化并分析它们。如果扰动项?很小，我们自然感觉（E1-1）和(E1-2)的系数的解应当相差很小。计算中你有什么出乎意料的发现？表明有些解关于如此的扰动敏感性如何？18?xE1-22（）将方程（）中的扰动项改成或其他形式，实验中又有怎样的现象出现？1实验步骤：（1）程序t_charpt1_1functionclcresult=inputdlg({'请输入扰动项:在[020]之间的整数:'},'charpt});'19'1_1',1,{Numb=str2num(char(result));if((Numb>20)|(Numb<0))errordlg('请输入正确的扰动项:[020]之间的整end;!');return数result=inputdlg({'请输入(01)之间的扰动常数:'},'charpt});'0.00001'1_1',1,{ess=str2num(char(result));ve=zeros(1,21);ve(21-Numb)=ess;root=roots(poly(1:20)+ve);x0=real(root);y0=imag(root););'*'plot(x0',y0',disp(['对扰动项',num2str(Numb),'加扰动',num2str(ess),'得到的全部根]);:'为disp(num2str(root));二、实验结果分析ess分别为1e-6,1e-8.1e-10,1e-12.对扰动项19加扰动1e-006得到的全部根为:21.3025+1.56717i21.3025-1.56717i18.5028+3.6004i18.5028-3.6004i15.1651+3.76125i15.1651-3.76125i12.4866+2.88278i12.4866-2.88278i10.5225+1.71959i10.5225-1.71959i9.04485+0.594589i9.04485-0.594589i7.9489+0i7.00247+0i5.99995+0i5+0i4+0i3+0i2+0i1+0i对扰动项19加扰动1e-010得到的全部根为:19.9953+0i19.0323+0i17.8696+0i17.2186+0i15.4988+0.0211828i15.4988-0.0211828i13.7707+0i13.1598+0i11.9343+0i11.029+0i9.99073+0i9.00247+0i7.99952+0i7.00007+0i5.99999+0i5+0i4+0i3+0i2+0i1+0iess分别为1e-6,1e-8.1e-10,1e-12的图像如下：2当的解相差很小，E.1.1和方程E.1.2从实验的图形中可以看出，当ess充分小时，方程逐渐增大时，方程的解就出现了病态解，这些解都呈现复共轭性质。ess18时方程的解都比较准确，没有出现复共轭现象。xess=1e-009上后，（2）将扰动项加到191819小一个数量级。对上比加到时误差与xx(ess=1e-009)时相当，即扰动加到xess=1e-0088时没有出现复共轭，x的扰动ess=10e10的扰动ess=1000时没有出现复共轭，误差很小；对xn上时，n误差很小。因此，扰动作用到x越小，扰动引起的误差越小。、2多项式插值的振荡现象，即插值的龙格（Runge）现象实验2。问题提出：拉格朗日插值中使用的节点越多，考虑在一个固定的区间上用插值逼近一个函数。显然，)(xL是否也更加靠近被逼插值多项式的次数就越高、自然关心插值多项式的次数增加时，n],1[?1...