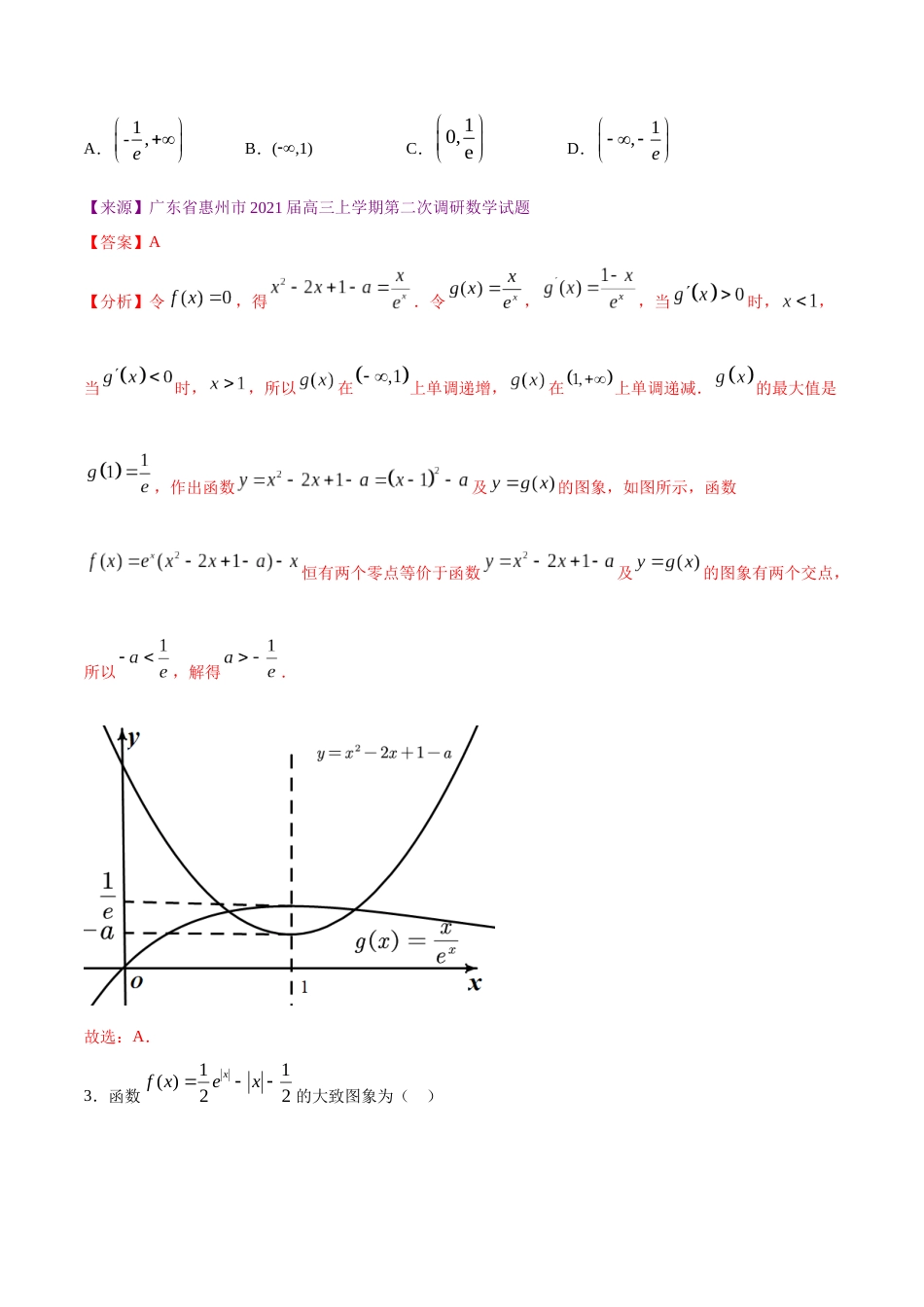
高三数学百所名校好题分项解析汇编之新高考地区专版(2021版)专题03导数一、单选题1．已知定义域为R的函数fx的图象连续不断，且xR，2()4fxfxx，当x0,时，4fxx，若221682fmfmmm，则实数m的取值范围为（）A．1,3B．1,C．1,3D．,1【来源】广东省广州市华南师范大学附属中学2020届高三上学期9月月考数学（理）试题【答案】A【分析】依题意，，故，令，可知，函数为奇函数.因为当时，，即当时，，故函数在上单调递减，由奇偶性可知，函数在上单调递减，因为，故，即，故，故，故实数m的取值范围为.故选：A.2．若函数f(x)=ex(x22x+1a)x恒有2个零点，则a的取值范围是（）A．-1,eB．(,1)C．10,eD．1,e【来源】广东省惠州市2021届高三上学期第二次调研数学试题【答案】A【分析】令，得．令，，当时，，当时，，所以在上单调递增，在上单调递减．的最大值是，作出函数及的图象，如图所示，函数恒有两个零点等价于函数及的图象有两个交点，所以，解得．故选：A．3．函数11()22xfxex的大致图象为（）A．B．C．D．【来源】河北省张家口市第一中学2021届高三（衔接班）上学期期中数学试题【答案】C【分析】因为函数的定义域为R，且，所以函数为偶函数，故排除B；又当时，，则，所以在上单调递减，在上单调递增，故排除AD.故选：C.4．已知函数2xfxxae在区间1,2上单调递增，则a的取值范围是（）A．3,B．,8C．3,D．8,【来源】福建省厦门市湖滨中学2021届高三10月月考数学试题【答案】A【分析】在区间上恒成立，则在区间上恒成立,即故选：A5．若函数2()xfxmxe恰有两个不同的零点，则实数m的取值范围为（）A．1,1eB．1,eC．(1,)eD．(,)e【来源】海南、山东等新高考地区2021届高三上学期期中备考金卷数学（A卷）试题【答案】B【分析】显然，0x不是函数()fx的零点，令2()0xfxmxe，得xe2mx，构造函数2()xegxx，0x，则22(1)()xexgxx，令()0gx得到x1，令()0gx得到1x且0x，即函数2()xegxx在,0上单调递减，在0,1上单调递减，在1,上单调递增；所以函数2()xegxx有极小值1g(1)e；画出函数()gx的图象，如图所示，由图像可知，当0m时，直线ym与()gx的图象不可能有两个交点，当m0，只需1me，()gx的图象与直线ym即有两个不同的交点，即函数2()xfxmxe恰有两个不同的零点，∴m的取值范围为1,e.故选：B.6．函数32()fxaxxcxd的图象如图所示，则有（）A．0,0,0acdB．0,0,0acdC．0,0,0acdD．0,0,0acd【来源】北京师范大学第二附属中学2021届高三10月月考数学试题【答案】C【分析】因为32()fxaxxcxd，所以232fxaxxc，由图象可知：fx先减后增再减，所以fx先为负，再为正，最后又为负，所以a0，因为1,2xx为fx的两个极值点，且12xx0，所以03ca，所以c0，又因为00f，所以d0，故选：C.7．点P在函数y＝ex的图象上．若满足到直线y＝x+a的距离为2的点P有且仅有3个，则实数a的值为（）A．22B．23C．3D．4【来源】北京市昌平区2020届高三第二次统一练习（二模）数学试题【答案】C【分析】过函数y＝ex的图象上点P（x0，y0）作切线，使得此切线与直线y＝x+a平行y′＝ex，于是01xe，则x0＝0，y0＝1∴P（0，1），于是当点P到直线y＝x+a的距离为2时，则满足到直线y＝x+a的距离为2的点P有且仅有3个，∴1211ad，解得a＝﹣1或a＝3又当a＝﹣1时，函数y＝ex的图象与直线y＝x﹣1相切，从而只有两个点到直线距离为2，所以不满足；故a＝3．故选：C．8．已知函数2()(1)sinfxaxax是奇函数，则曲线()yfx在点(0，0)处的切线斜率为（）A．2B．﹣2C．1D．﹣1【来源】江苏省无锡市2020-2021学年高三上学期期中数学试题【答案】D【分析】由题意函数...