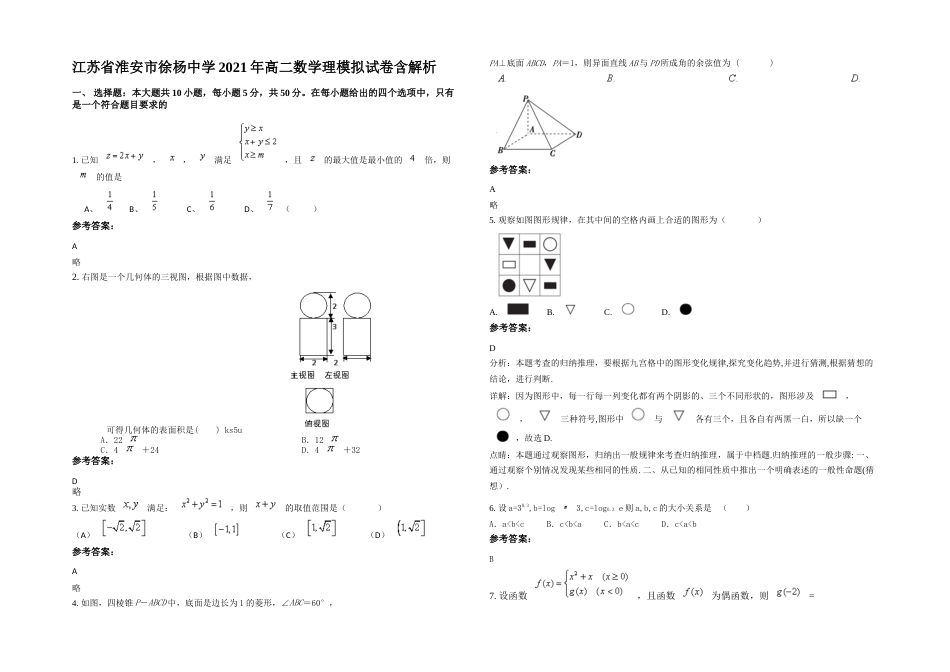
江苏省淮安市徐杨中学2021年高二数学理模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.已知，，满足，且的最大值是最小值的倍，则的值是A、B、C、D、（）参考答案：A略2.右图是一个几何体的三视图，根据图中数据，可得几何体的表面积是()ks5uA．22B．12C．4＋24D．4＋32参考答案：D略3.已知实数满足：，则的取值范围是（）（A）（B）（C）（D）参考答案：A略4.如图，四棱锥P－ABCD中，底面是边长为1的菱形，∠ABC＝60°，PA⊥底面ABCD，PA＝1，则异面直线AB与PD所成角的余弦值为()参考答案：A略5.观察如图图形规律，在其中间的空格内画上合适的图形为（）A.B.C.D.参考答案：D分析：本题考査的归纳推理，要根据九宫格中的图形变化规律,探究变化趋势,并进行猜测,根据猜想的结论，进行判断.详解：因为图形中，每一行每一列变化都有两个阴影的、三个不同形状的，图形涉及，，三种符号,图形中与各有三个，且各自有两黑一白，所以缺一个，故选D.点睛：本题通过观察图形，归纳出一般规律来考查归纳推理，属于中档题.归纳推理的一般步骤:一、通过观察个别情况发现某些相同的性质.二、从已知的相同性质中推出一个明确表述的一般性命题(猜想）.6.设a=30.3,b=log3,c=log0.3e则a,b,c的大小关系是（）A．a<b<cB．c<b<aC．b<a<cD．c<a<b参考答案：B7.设函数，且函数为偶函数，则=A．6B．—6C．2D．—2参考答案：A8.某公司准备进行两种组合投资，稳健型组合投资是由每份金融投资20万元，房地产投资30万元组成；进取型组合投资是由每份金融投资40万元，房地产投资30万元组成。已知每份稳健型组合投资每年可获利10万元，每份进取型组合投资每年可获利15万元。若可作投资用的资金中，金融投资不超过160万元，房地产投资不超过180万元，要使一年获利总额最多，则稳健型组合投资与进取型组合，合投资分别注入的份数分别为（）A.x=4,y=2B.x=3,y=3C.x=5,y=1D.x=5,y=2参考答案：A9.在△ABC中，内角A，B，C所对的边分别是a，b，c，若c2=（a﹣b）2+6，C=，则△ABC的面积是（）A．B．C．D．3参考答案：C【考点】余弦定理．【专题】解三角形．【分析】将“c2=（a﹣b）2+6”展开，另一方面，由余弦定理得到c2=a2+b2﹣2abcosC，比较两式，得到ab的值，计算其面积．【解答】解：由题意得，c2=a2+b2﹣2ab+6，又由余弦定理可知，c2=a2+b2﹣2abcosC=a2+b2﹣ab，∴﹣2ab+6=﹣ab，即ab=6．∴S△ABC==．故选：C．【点评】本题是余弦定理的考查，在高中范围内，正弦定理和余弦定理是应用最为广泛，也是最方便的定理之一，高考中对这部分知识的考查一般不会太难，有时也会和三角函数，向量，不等式等放在一起综合考查．10.下列求导运算正确的是（）A．(x+B．(log2x)′=C．(3x)′=3xlog3eD．(x2cosx)′=-2xsinx参考答案：B二、填空题:本大题共7小题,每小题4分,共28分11.过点P（1,2）引直线使A（2，3），B（4，5）到直线的距离相等，求这条直线方程_____________参考答案：或12.在8和36之间插入6个数，使这8个数成等差数列，则插入的6个数是参考答案：12,16,20,24,28,3213.已知数列,…,计算得,….由此可猜测=.参考答案：14.若P表示已知条件或已有的定义、公理或定理，Q表示所得到的结论，下列框图表示的证明方法是．参考答案：综合法【考点】综合法与分析法(选修）．【分析】根据证题思路，是由因导果，是综合法的思路，故可得结论．【解答】解： P表示已知条件或已有的定义、公理或定理，Q表示所得到的结论，∴证明方法是由因导果，是综合法的思路故答案为：综合法15.一个箱子中装有6个白球和5个黑球，如果不放回地依次抽取2个球，则在第1次抽到黑球的条件下，第2次仍抽到黑球的概率是_________．参考答案：16.若数列{an}前n项和，则a6=．参考答案：11【考点】数列递推式．【专题】计算题；函数思想；数学模型法；等差数列与等比数列．【分析】由已知，直接利用a6=S6﹣S5求得答案．【解答】解：由，得．故答案为：11．【点评】本题考查数列递推式，训练了由数列的前n项和求数列的项的方法，是基础题．17.为了研究某种细菌在特定环境下随时间变化的...