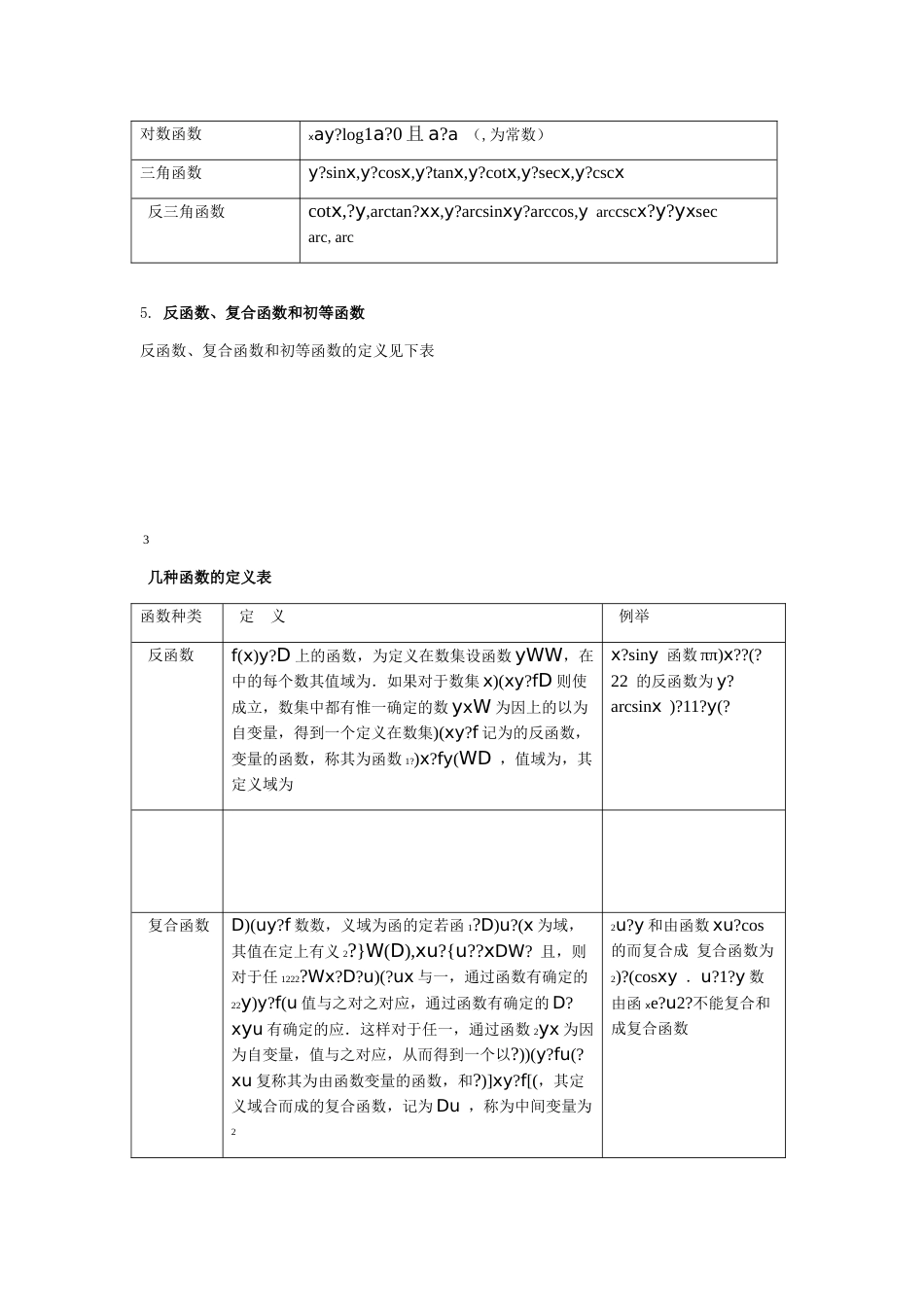
函数第一章一、本章学习要求与内容提要（一）学习要求理解函数的概念．1.了解分段函数、基本初等函数、初等函数的概念．2..了解反函数、复合函数的概念，会分析复合函数的复合结构3..会建立简单实际问题的函数模型4..函数的概念、复合函数和初等函数的概念，会求函数的定义域重点.分段函数的概念，建立简单实际问题的函数模型难点内容提要（二）函数的定义1.函数的定义(1)xyyDx?D按,1设如果对于每个数和变量是两个变量,是一个给定的数集,定义xy)xf(y?D称为的函数,则称记作是.数集照一定法则总有惟一确定的数值与其对应,yx.称为因变量该函数的定义域,称为自变量,xxxy)xy?f(f在点按照法则时，因变量当自变量所取定的数值称为函数取数值00)(xfxD对应的函数值的全体组处的函数值，记作的每个数值时遍取定义域,.当自变量0??D),x?yy?f(xW.=成的数集称为函数的值域fDDB中任何一与，使得对2设是两个非空实数集，如果存在一个对应规则定义xxyfDB上的函数，记对应，则对应规则中都有惟一确定的实数个实数称为在，在与为BD?或f:f:x?y,xy称为对应的函数值，记为D?),xy?f(x,xy.称为自变量，其中，称为因变量)(x(fx)fy?f是对应,函数是一种对应规则，在函数表示函数，中，由定义2知x所以习但在研究函数时，于自变量这种对应关系总是通过函数值表现出来的，的函数值，xxyy)f(xy?但应正确理.是惯上常把在的函数处的函数值的形式表示称为函数，并用23）xf?4x?10(?xff例如解，函数的本质是指对应规则就是一个特定的函数，.确定的对应规则为2310??4()f()?().就是一个函数(2)函数的两要素xy)(x?yffD来确的定义域函数又是由对应规则是自变量的取值范围，而函数值fD所确定的，因此通常称函数的定义域和对应规则定的，所以函数实质上是由其定义域也就是说，只要两个函数的定义域相同，对应规则也相同，和对应规则为函数的两个要素.2v?与z?yx，就是相就称这两个函数为相同的函数，与变量用什么符号表示无关，如.同的函数函数的三种表示方法2．图像法(1)1这种方法直观简称图像法.用函数的图形来表示函数的方法称为函数的图像表示方法,但根据函数图形所求出的函数值准确度不高且不便于作理论,性强并可观察函数的变化趋势.研究表格法(2)将自变量的某些取值及与其对应的函数值列成表格表示函数的方法称为函数的表格表这种方法的优点是查找函数值方便，缺点是数据有限、不直观、不便.,简称表格法示方法.于作理论研究公式法(3),简称公式法，也称为用一个（或几个）公式表示函数的方法称为函数的公式表示方法这种方法的优点是形式简明，便于作理论研究与数值计算，缺点是不如图像法来得解析法..直观在用公式法表示函数时经常遇到下面几种情况：分段函数①.如在自变量的不同取值范围内，用不同的公式表示的函数，称为分段函数,?01,xx???2,2?0xx)?x?,f(??,5?x?lnx,2?]5(??,就是一个定义在区间上的分段函数.用参数方程确定的函数②)t??(x?Ι?t）（用参数方程?)t??(y?xy例如函数表示的变量之间的函数关系，称为用参数方程确定的函数与.cost?2y??)0?t?()]?1,1?1?xx(?[y可以用参数方程.表示?sint?③隐函数x0)?x,yF(在某区间I内任意取定一个值时，相应地总有满足该中，当如果在方程yF(x,y)?0在区间I内确定了一个隐函数方程的惟一的.值存在，则称方程例如方程x?xy?1e?0xy之间的函数关系.是变量就确定了变量x)(xx)f(y?f的解析式)的形式的函数,能表示成注意称为显函数仅为.把其中(x01??exy?可以化成显函数隐函数的显化一个隐函数化成显函数的过程称为.例如xe?1xyy?e?xy?e?0..,例如但有些隐函数确不可能化成显函数x23．函数的四种特性y?f(x)D，函数的四种特性如下表所示设函数的定义域为区间.函数的四种特性表函数的特性定义图像特点奇偶性)xy?f(D?xD满关于原点对称，设函数若对任意的定义域)),f(xf(?x)?f(xDx?D满足是上的偶函数；若对任意则称)(x??f(x),ff(?x)D上的奇函数，既不是奇函数也则称是足不是偶函数的函数，称为非奇非偶函数偶函数的图y轴对形关于称;奇函数的图形关于原点对称单调性)f(x)?x,x(a,b)x?xf(x?,时，有，当若对任意211221x?x)?yf(x)(a,b时，则称函数是区间上的单调增加函数；当21f(x)f(x)y?f(x)(a,b)?上的...