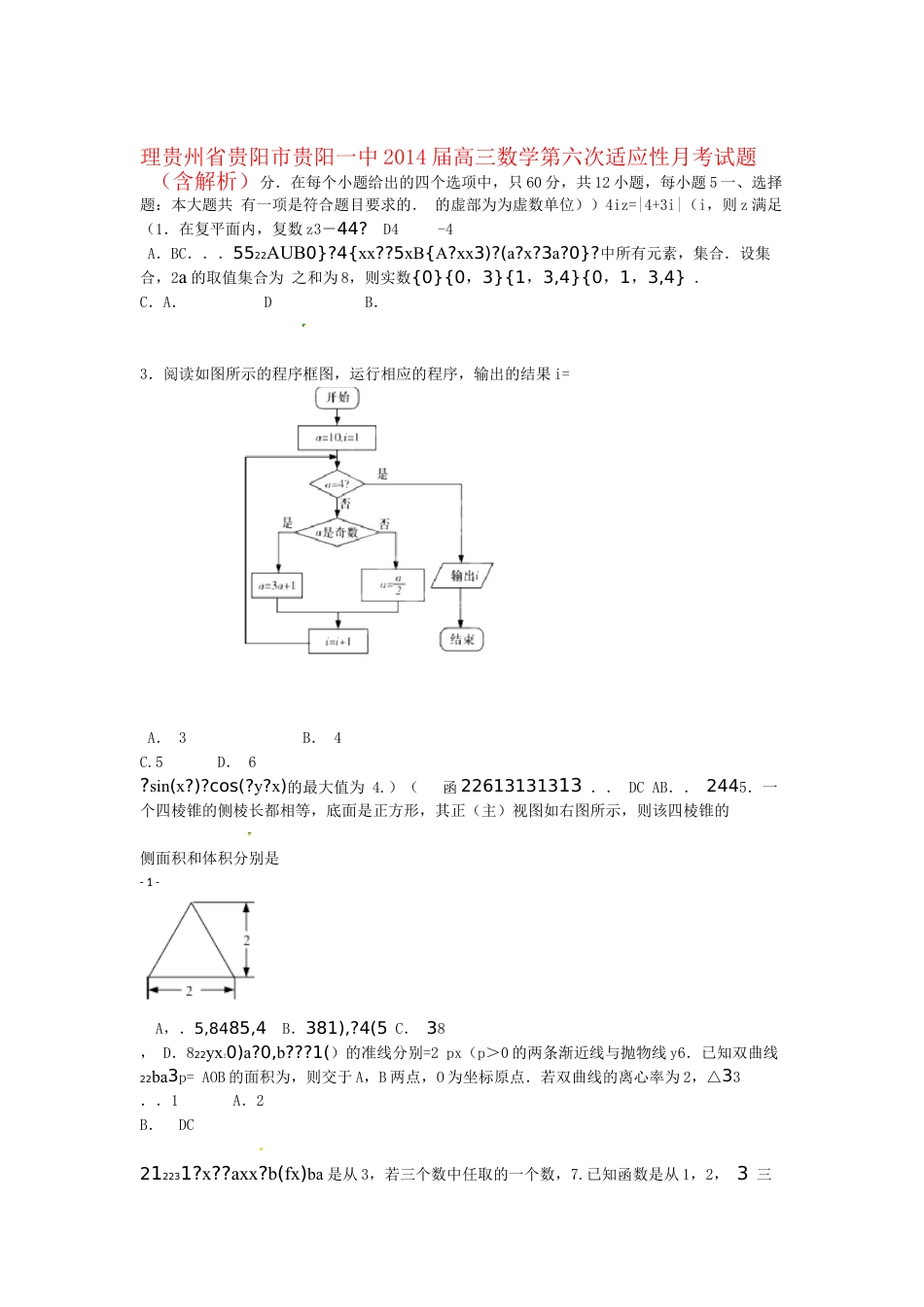
理贵州省贵阳市贵阳一中2014届高三数学第六次适应性月考试题（含解析）分．在每个小题给出的四个选项中，只60分，共12小题，每小题5一、选择题：本大题共有一项是符合题目要求的．的虚部为为虚数单位））4iz=|4+3i|（i，则z满足（1．在复平面内，复数z3－44?D4-4A．BC．．．5522AUB0}?4{xx??5xB{A?xx3)?(a?x?3a?0}?中所有元素，集合．设集合，2a的取值集合为之和为8，则实数{0}{0，3}{1，3,4}{0，1，3,4}．C．A．DB．3．阅读如图所示的程序框图，运行相应的程序，输出的结果i=A．3B．4C.5D．6?sin(x?)?cos(?y?x)的最大值为4.）（函22613131313．．DCAB．．2445．一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如右图所示，则该四棱锥的侧面积和体积分别是-1-A，．5,8485,4B．381),?4(5C．38，D．822yx20)a?0,b???1(）的准线分别=2px（p＞0的两条渐近线与抛物线y6．已知双曲线22ba3p=AOB的面积为，则交于A，B两点，O为坐标原点．若双曲线的离心率为2，△33．．1A．2B．DC212231?x??axx?b(fx)ba是从3，若三个数中任取的一个数，7.已知函数是从1，2，3三个数中任取的一个数，则该函数有两个极值点的概率为()，0，122715D.B.C.A.33991AC?BE?o的长，则E8．在平行四边形ABCD中，AD=1，∠BAD=60，为CDAB的中点．若为112．1．DC．BA．24??*naa?a?aNn?且，）定为意的均有值9.在数列（对中，若任n2n?n?n1??a?a?4S?a2,a?3,），则数列（的前100项的和n10098799968132299DC．．A．B．0?y?1?3x??0?3m?xx－，满足，y的不等式组x，y）（，表示的平面区域内存在点P．10设关于x?000?0m?y??3y的取值范围是m=3，求得01111??)),,(???)??(???(,A．．B．D．C,????2233??-2-x?x，xx11．函数f（）的定义域为D，若对于任意，xD，当f（（时，都有fx）≤x）?221121上为非减函数，且满足以下则称函数f（[0，1]）在减函数．设函数）在D上为非f（xx111x??????）x－f（=1l；③；（三个条件：①f0）=0②，则f（－x）ff?)fxf?(??????8323??????等于234．BC．．1D．A3451xx?的y=m=ln）的图象分别与直线交于A，|AB|B两点，则gxf12．已知函数（）=e，（x22最小值为13?2－C．e2+ln2B．D2A．．2eln22分，共小题，每小题4520分。把答案填在答题卡的相应位置。填空题：本大题共二.n|?4f(x)|?x?2||?x12xn)(?x项的系数的最小值为13、已知，则二项式展开式中x.为ABCDP??PA的正方形，且底面1ABCD四棱锥14、是边长为的五个顶点都在一个球面上，2?PA，则该球的体积为_，ABCD．平面ABCa、b、cA、B、C的对边，且分别是角15、在锐角三角形．中，0sinA?3a?2cab的最大值为_.＋若，则2c?22yxPACPACA－上且直线斜率的取值范围是在[116、椭圆：＋＝的左、右顶点分别为、，点21234PA斜率的取值范围是，那么直线2，－1]1分．解答应写出文字说明，证明过程或演算步骤三、解答题：本大题共6小题，共7018．某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导-3-也可以放每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,讲座,否则称为不满,各科达到预先设定的人数时称为满座弃任何一门科目的辅导讲座.(规定::统计数据表明座各学科讲座各天的满座概率如下表),技信息生物化学物理数学术11111周一2444421111周三3222221111周五33333(Ⅰ)求数学辅导讲座在周一、周三、周五都不满座的概率;??的分布列和数学期望求随机变量(Ⅱ)设周三各辅导讲座满座的科目数为.,oABC90BCA???PBABC?P，，底面中，19.如图，三棱锥PB?BC?CA?2PCFPA2PF?FAE.的中点，点，上，且为在PAC?BEF；(Ⅰ)求证：平面平面ABCBEF所成的二面角的平面角与平面)求平面(Ⅱ（锐角）的余弦值.F(?1,0),F(1,0)PF?PF?22PP记点满足20、已知，为平面内的两个定点，动点2121C．的轨迹为曲线C的方程；（Ⅰ）求曲线OA、B、CCOA?OB?OC?0．是曲线为坐标原点，点（Ⅱ）设点上的不同三点，且OCABAB过（ⅰ）试探究：直线的斜率之积是否为定值？证明你的结论；与（ⅱ）当直线xOCFAB轴所围成的三角形的面积．与、点时，求直线1k2x,(k?0,且k?1(x)?ln(?x)?x?1)f．21、...