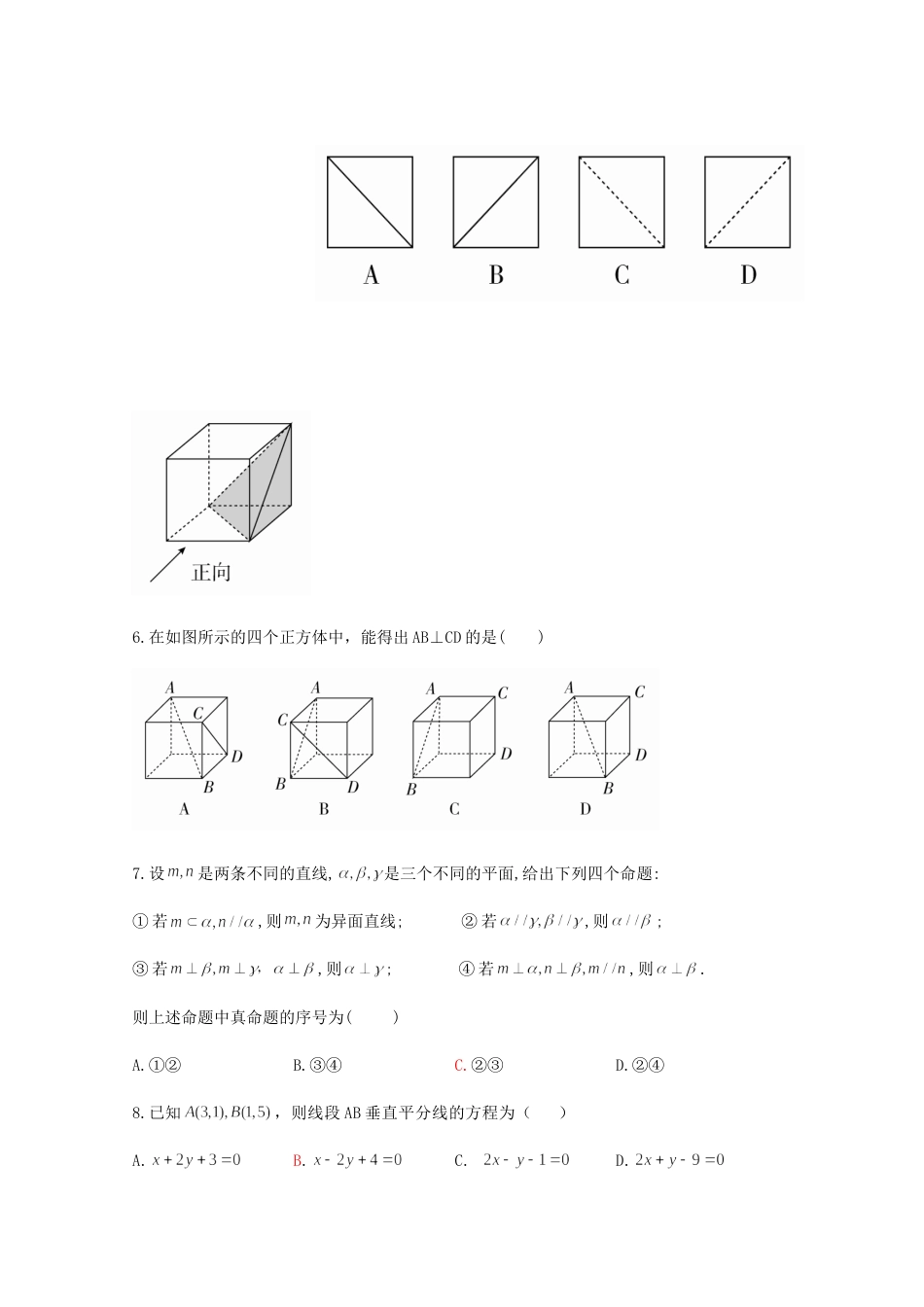
四川省眉山市彭山区第一中学2020-2021学年高二数学10月月考试题文一、选择题（每题5分，共60分）1.用一个平面去截一个几何体，得到的截面是三角形面，这个几何体不可能是()A．棱锥B．圆锥C．圆柱D．正方体2下列说法正确的是()A．垂直于同一条直线的两条直线平行B．垂直于同一条平面的两条直线平行C．平行于同一个平面的两条直线平行D．平行于同一个直线的两个平面平行3.已知过点的直线的斜率为,则()A.2B.4C.D.4.已知水平放置的按"斜二测画法"得到如图所示的直观图,其中,那么是一个()A.等边三角形B.直角三角形C.等腰三角形D.钝角三角形5.如图是正方体截去阴影部分所得的几何体，则该几何体的侧视图是()6.在如图所示的四个正方体中，能得出AB⊥CD的是()7.设是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则为异面直线;②若,则;③若,则;④若,则.则上述命题中真命题的序号为()A.①②B.③④C.②③D.②④8.已知，则线段AB垂直平分线的方程为（）A.B.C.D.9.有一根蜡烛点燃6min后，蜡烛长为17.4cm;点燃21min后，蜡烛长为8.4cm.已知蜡烛长度(cm)与燃烧时间t(min)可以用直线方程表示，则这根蜡烛从点燃到燃尽共耗时()A.25minB.35minC.40minD.45min10.在正三棱柱中,侧棱长为,底面三角形的边长为1,则与侧面所成角的大小为()A.B.C.D.11.已知为球的球面上的三个点，圆O1为的外接圆，若圆O1的面积为，，则球的表面积为()A.B.C.D.12.动点在正方体的对角线上,过点作垂直于平面的直线,与正方体表面相交于点设则函数的图象大致是()A.B.C.D.二、填空题（每题5分，共20分）13.已知三点A（2，3）、B（-1,2)、C（5，m)共线，则m=________.14已知直线l经过点A.且它的倾斜角是直线的倾斜角的两倍，则直线l的斜截式方程为．15.如图所示，扇形的中心角为90°，弦AB将扇形分成两个部分,这两部分各以AO为轴旋转一周，求这两部分旋转所得旋转体体积和之比为__________.16.如图，矩形中，，为边的中点，沿将折起，点折至处（平面），若为线段的中点，则在折起过程中，下列说法正确的是。①．始终有平面②．存在某个位置，使得A1E平面A1DC③．异面直线与所成角的大小与点A1的位置有关④．点在某个球面上运动三、解答题.（共70分，写出必要的解题步骤和文字说明）17.（10分）如图，在中，点A（3，0），点C（1，3）．（1）求AB所在直线的方程；（2）过点C做CD⊥AB于点D，求CD所在直线的方程．DBCAO1xy18.（12分）如图，在三棱锥P－ABC中，PA⊥底面ABC，D是PC的中点．已知∠BAC＝，AB＝2，AC＝2，PA＝2.求：(1)三棱锥P－ABC的体积；(2)异面直线BC与AD所成角的余弦值．19.（12分）已知直线l过点(1,4)，且在x、y轴上的截距依次为a和b,(1)若a与b互为相反数,求直线的l方程;(2)若a>0,b>0,当a+b取得最小值时,求直线l的方程。20.（12分）如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上的点．AB=4，BC=3，∠MDC=30°。①证明：平面AMD⊥平面BMC；②求直线AM与面ABCD所成角的正切值。21.（12分）如图所示，四棱锥P－ABCD的底面是边长为8的正方形，四条侧棱长均为2.点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥平面GEFH.(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH的面积。22.（12分）如图，四棱锥P－ABCD中，PD⊥底面ABCD，AB∥CD，∠BAD＝，AB＝1，CD＝3，M为PC上一点，且MC＝2PM.(1)证明：BM∥平面PAD；(2)若AD＝2，PD＝3，求点D到平面PBC的距离。彭山一中高2022届高二（上）10月月考数学（文科）参考答案一选择题题号123456789101112答案CBDACACBBADD二、填空题13.414.15.16.①④17.(1)y=3x-9(2)x+3y-10=018.答案：(1)S△ABC＝×2×2＝2，三棱锥P－ABC的体积为V＝S△ABC·PA＝×2×2＝.(2)如图，取PB的中点E，连接DE，AE，则ED∥BC，所以∠ADE(或其补角)是异面直线BC与AD所成的角．在△ADE中，DE＝2，AE＝，AD＝2，cos∠ADE＝＝.故异面直线BC与AD所成角的余弦值为.19.解：（1）若a=0,b=0，则可设，，此时，若，则可设，从而有，此时，综上，直线。（2），当且仅当，由20.①证明：由题设知，平面CMD⊥平面ABCD，交线为CD.因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，故BC⊥DM...