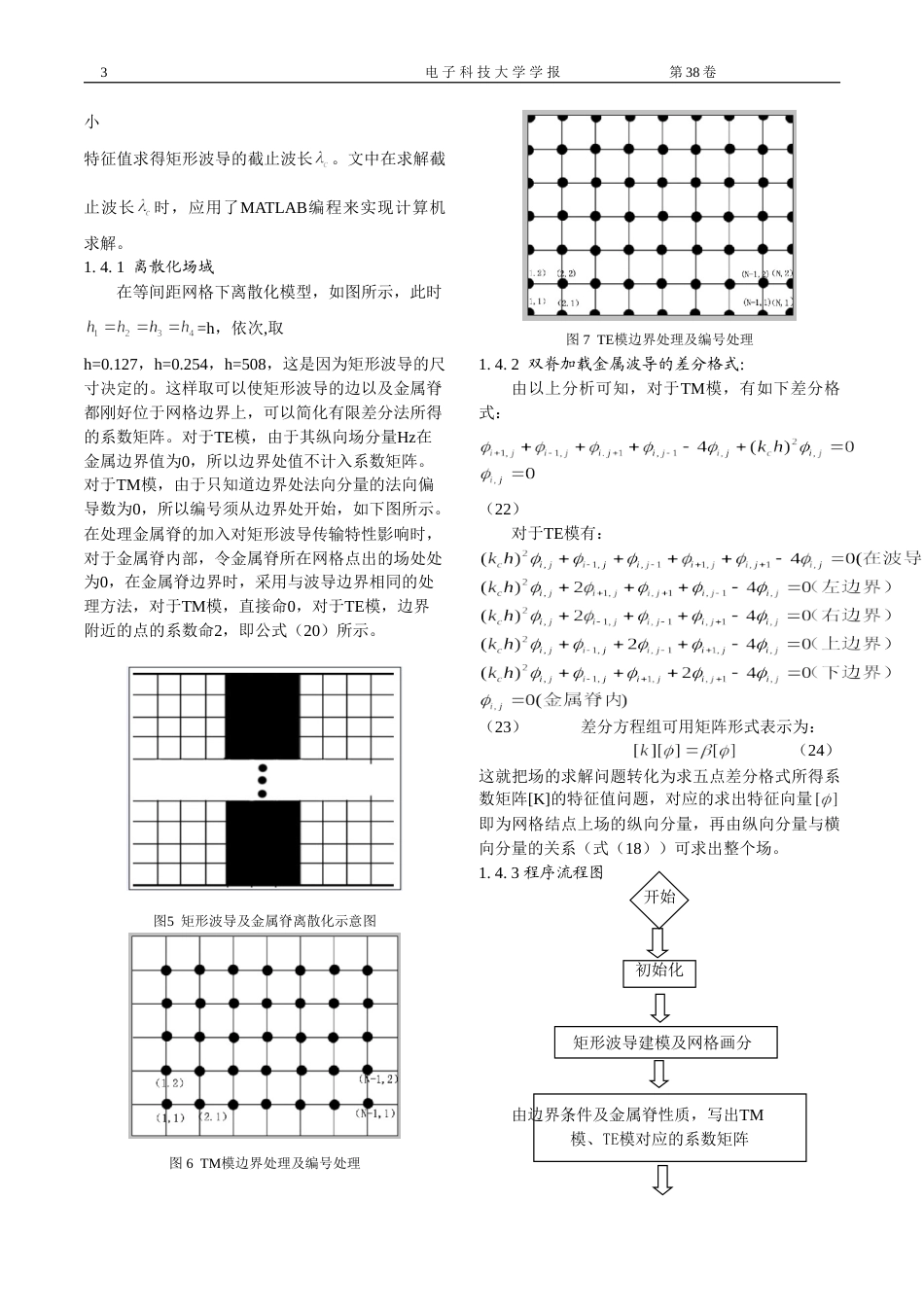
第38卷第5期电子科技大学学报Vol.38No.52013年4月JournalofUniversityofElectronicScienceandTechnologyofChinaapril.2013双脊金属加载矩形波导的基模及第一个高阶模的色散特性分析XXX电子科技大学物理电子学院,成都,610054【摘要】利用有限差分法，对双脊金属加载矩形波导的基模及第一个高阶模的色散特性进行了分析研究，得出了模式的横截面电磁场分布图，并研究了网格粗细对计算结果的影响。最后通过与CST、HFSS软件仿真的仿真的结果对比，验证了结果的正确性。关键词:双脊；矩形波导；有限差分；模式；色散曲线；场分布TN252文献标识码AResearchonTheFundamentalModeandThefirsthigh-ordermodeofDouble-ridgedMetalLoadedRectangularWaveguideLI激ang激angSchoolofPhysicalElectronics,UniversityofScienceandTechnologyofChina,Chengdu,610054Abstract:Inthispaper,thefundamentalmodeandahigherordermodeofdouble-ridgedmetalloadedrectangularwaveguidewascalculatedbyusingthefinitedifferencemethod.Thecross-sectiondistributionoftheelectromagneticfieldwasstudiedaswell.Atlast,toprovethecorrectnessoftheresults,wecomparedtheresultobtainedinmatlabwithitobtainedinCSTandHFSS,andtheymatchedwell.Keywords:doubleridges;rectangularwaveguide;finitedifferential;mode;dispersioncurve;fielddistribution引言有限差分法是一种求微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。本文重点讨论用有限差分法求解双脊金属加载矩形波导的电磁场问题，通过matlab编程得到了基模和第一高次模的色散特性曲线，并画出了基模和第一高次模的电场磁场图，分析了网格疏密对结果的影响，最后通过CST仿真软件，验证了结果的正确性。1.有限差分法有限差分法是以差分原理为基础的一种数值计算法。它用离散的函数值构成的差商来近似逼近相应的偏导数,而所谓差商则是基于差分应用的数值微分表达式。1.1差分运算基本概念下函数f(x)，变量x有增量=h，则有：(1)所以，称为f(x)的一阶差分，则一阶差商为：(2)若→0，即h→0，则有一阶倒数：(3)同理二阶导数：电子科技大学学报第38卷(4)1.2差分格式的建立如图1所示，设变量在边界c构成的场域D中。图1等步长区域的网格划分图首先将场域D离散化，此处采用有规律的划分方式，使每个离散节点均可得出相同形式的差分方程,从而提高求解速度。1.2.1一阶差分偏导数的中心差分格式设分别表示0、1、2、3、4处的函数值,则点0处x轴方向的前向差分为：（5）后向差分为：（6）事实证明无论是前向差分还是后向差分都存在很大的误差，现在要寻求一种较精确的差分格式，引入常数α、β对和进行泰勒展开:（7）令二次项项系数为，得：（8）将式(7)代入到式(6)中，并舍去高阶项，得：（9）等步长下，，有：（10）这就是所需要的x轴中心差分表达式。同理对于y轴方向，它的中心差分表达式应由决定,即（11）1.2.2二阶差分偏导数的中心差分格式在式(6)中,令项系数为0，则有：（12）将式（11）代入式（6）中，舍去高阶项，得：（13）在等步长时，有：（14）同理对于y轴方向，它的中心差分应由决定，即：（15）1.2亥姆霍兹方程的有限差分形式亥姆霍兹方程：将式（14）和式（15）代入上式，得：1第1期李江江：金属加载矩形波导基模及第一高次模色散特性分析（16）那么任意节点(i,j)的亥姆霍兹方程的差分格式为：（17）1.3有限差分法在矩形波导中的运用矩形波导中可以传输TE波和TM波,但这两类波所适用的边界条件不一样,所以首先讨论边值问题。这里先给出用场的纵向分量表示的横向分量公式，如式（18）所示。1.3.1第一类边界条件第一类边界条件是指在矩形金属波...