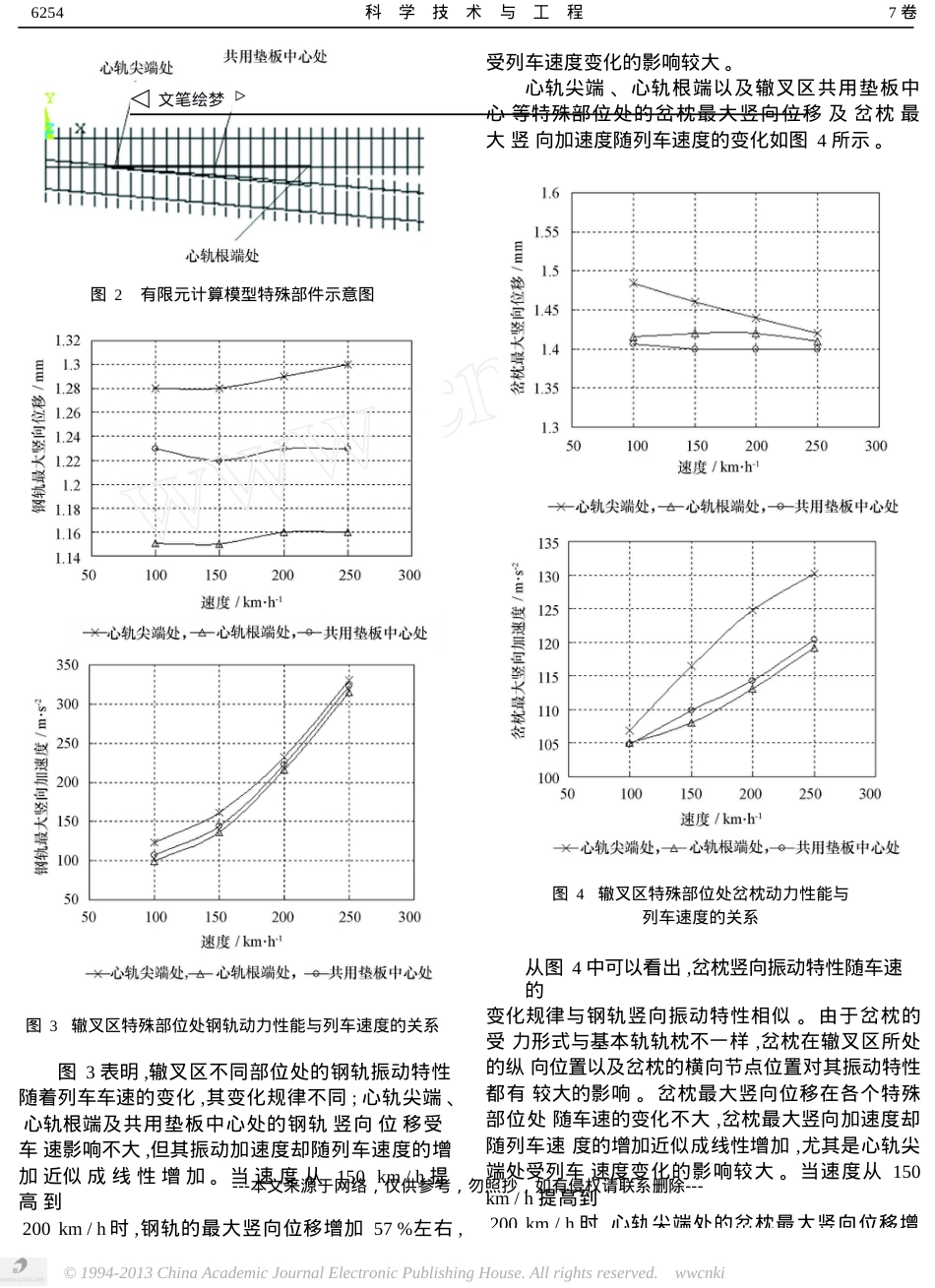
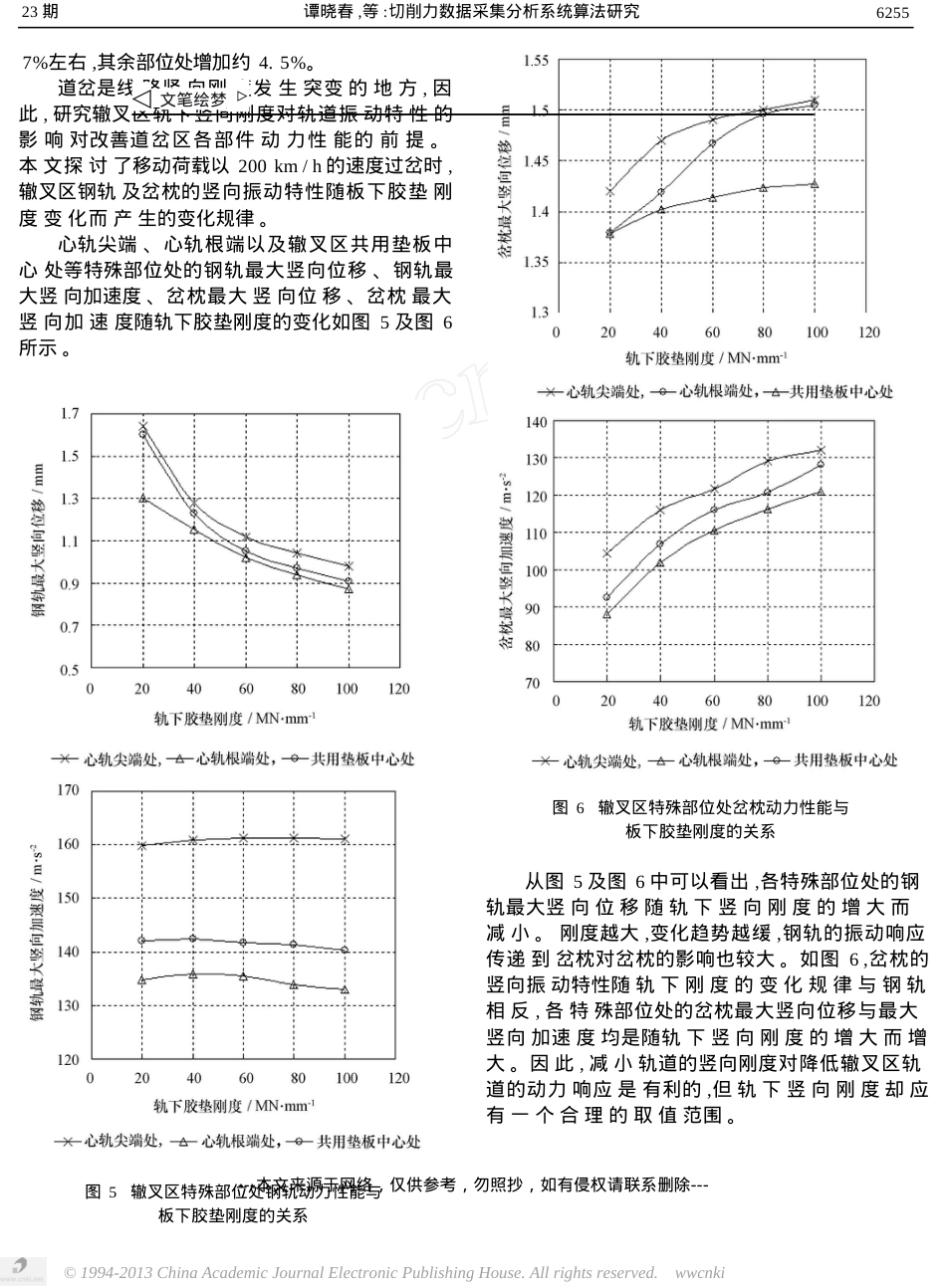
交通运高速道岔辙叉区动力响应仿真分析谭晓春罗雁云(同济大学铁道与城市轨道交通研究院,上海201804)摘要通过建立列车过岔有限元模型,运用动力学原理,研究移动荷载作用不同轨下刚度和列车速度在道岔辙叉区对轨道振动特性的影响。分析了心轨尖端、心轨根端及辙叉区共用垫板中心等特殊部位处的轨道振动特性。计算表明列车速度的变化对钢轨最大竖向加速度和岔枕最大竖向加速度的影响较大,而辙叉区轨下刚度的变化对钢轨最大竖向加速度、岔枕最大竖向位移及岔枕最大竖向加速度有较大的影响。关键词轨道刚度轨道振动道岔有限元中图法分类号U215.57;文献标识码A道岔是高速铁路发展的薄弱环节之一,大量试验表明,高速列车通过道岔区时,附加动力作用明显增加,势必加剧轮轨系统动力响应,增大岔区轨道部件的动应力,缩短其使用寿命;轻则影响车辆通过时的舒适性,重则形成安全隐患。因此,道岔区车辆通过性能方面的研究倍受关注[5],但国内外有关轨道动力性能的研究一般只限于区间线路,较少涉及道岔区。这一方面是由于以往列车的运行速度不高,另一方面是由于道岔区结构复杂,计算难度较大。本文试图从理论上探讨列车过岔时对轨道动力性能的影响。运用Ansys仿真软件建立道岔辙叉区动力分析有限元模型,研究不同列车速度和轨下刚度在辙叉区对轨道振动响应的影响。算难度较大。与基本轨相比,道岔区内钢轨的一个主要受力特点是:长岔枕的偏心受载和弯曲变形,致使非承载钢轨也间接地分担着一部分列车荷载,对承载钢轨起着帮轨作用。其动力方程如式(1)所示。u¨+u+Ku=F(1)MC(1)式中[M],[C]和[K]表示质量、阻尼及刚度矩阵。{u}表示位移向量,{F}表示合力。根据道岔的复杂结构,岔区内所有的梁单元均采用欧拉梁假定,不计轴力和剪切影响。钢轨梁单元均为双向可弯的弹性梁,岔枕梁单元为可弯的弹性梁。由于双向可弯梁单元的垂向和横向位移不耦合,因而单元刚度和质量矩阵可按单向可弯梁推导,并按节点位移顺序组建。单向可弯的有限梁单元的节点位移列阵、形函数及单元内任意一点的位移为:1道岔辙叉区动力分析模型ewi,θi,wi+1,θi+1Tu==,NN1,N2,N3,N4,1.1岔区轨道结构有限元控制方程[2,3]在道岔区,轨道结构型式比区间线路复杂,计e()wx=Nu2(2)式中,N1～N4为单元形函数,wi与θi为梁单元第i节点的线位移和转角。梁单元内任一点的位移表征为该点位置的三次函数:2007年8月16日收到第一作者简介:谭晓春(1983—),女,同济大学铁道与城市轨道交通研究院硕士研究生。---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---23期谭晓春,等:切削力数据采集分析系统算法研究625323运用有限元法,建立如图1所示的道岔辙叉区动力响应分析模型。基本轨、间隔铁、滑床台、间隔铁和铁垫板均采用等截面梁beam188单元模拟。钢轨在道岔辙叉区的心轨部分是变截面的,因此,心轨截面变化区段采用变截面梁单元模拟。实际钢轨的断面比较复杂,在不影响计算结果或定性分析的前提下,等截面区段的钢轨截面采用工字梁模拟;并采用标准轨距1.435m。在模型中,钢轨扣件被简化为一个连接在钢轨底部和铁垫板之间的一个无质量线性弹簧元件,刚度为扣压件和轨下胶垫的并联刚度,用combin14单元模拟。轨下弹性垫板被简化为一个连接在铁垫板底部和轨枕承轨槽之间的多个无质量的线性弹簧元件,它们的刚度之和等于板下胶垫刚度。轨枕可以被简化成支承在弹性地基上Euler梁,在模型中用弹性地基梁bea4单元来模拟并设置弹性地基梁的轨下刚度来表示轨枕支承在具有一定弹性的道床上,并考虑道床的横向阻力。为了便于建模,对轨枕的几何外形进行一定的简化,不考虑承轨槽的影响。wx=a0+a1x+a2x+a3x(3)(3)式中,a0～a3为常系数,可由单元的边界条件确定dwx=0,w=wi,θ=dx=θi(4)dwx=L,w=wi+1,θ==θi+1dx(4)式中,L为梁单元长度。由式(2)、式(3)、式(4)可得梁单元的形函数为:23xxN1=1-3+2LLx2xN2=1-2+LL(5)x2xN3=3-2LL2xxN4=-LL根据虚功原理和梁材料的应力应变关系,即可导出各种有限梁单元的刚度和质量矩阵。1.2有限元计算模型[4]相对区间线路轨道,岔区轨道结构要复杂得多。在道岔范围内,尤其是辙叉区部分,具有轨道部件多、轨道结构多样化等特征。钢轨件有多种型式,轨枕...