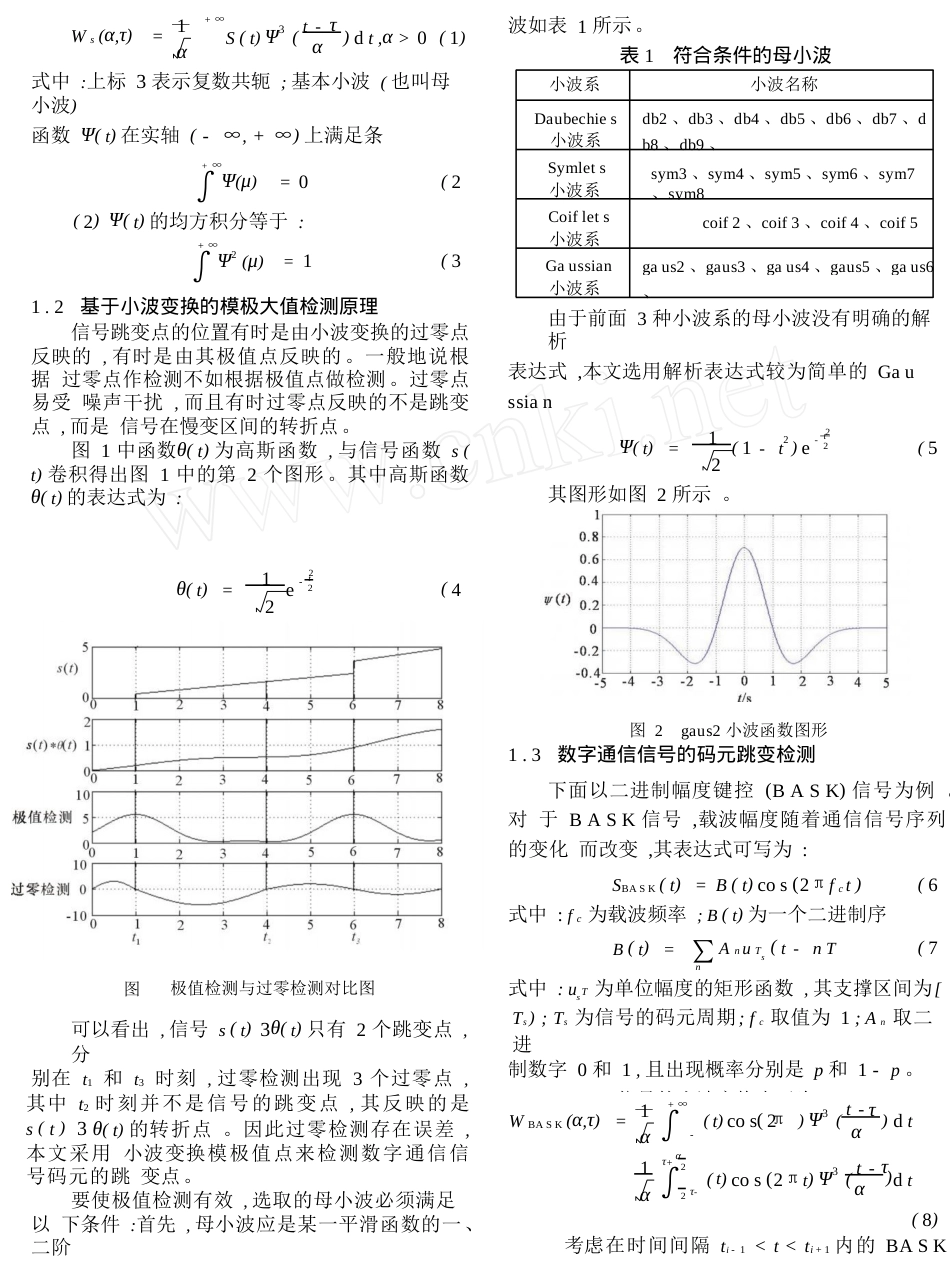
2009年2月第32卷第1期舰船电子对抗Feb.2009Vol.32No.1数字信号基于小波变换的码元符号率检测高翔,李敬辉,黄高明(海军工程大学,武汉430033)摘要:数字信号在码元边界上由于幅度、频率或相位的变化而产生变化。小波变换对信号的跳变点和奇异点有很好的检测能力。利用小波变换的模极大值方法可以对码元的跳变点进行检测,通过分析码元的跳变点进而可分析出码元的符号率。计算机仿真结果表明,该方法对码元的跳变点检测具有很高的精确性,能够比较准确地识别出码元符号率。关键词:小波变换;码元跳变点;模极大值;符号中图分类号:TN911.72文献标识码:A文章编号:CN3221413(2009)0120096204CodeElementSymbolRateDetectionofDigitalSignalBasedonWaveletTransformGAOXiang,LIJing2hui,HUANGGao2ming(UniversityofNavyEngineering,Wuhan430033,China)Abstract:Digitalsignalchangesontheboundaryofcodeelementbecauseofmagnitude,frequencyorphasechanges.Thewavelettransformhasperfectdetectionabilitytothejumppointsandoddpointsofsignal.Thejumppointsofcodeelementcanbedetectedbymeansofthemodelmaximummethod,symbolratioofcodeelementcanbeanalyzedthro岩岩利用小波变换的模极大值对信号进行分析,前者利用小波变换的模极大值检测故障点,后者利用小波变换的模极大值对图像信号进行处理。在同一码元内或者相邻码元相同时,信号小波变换的幅度为恒定值。如果在小波变换区间存在码元的变化,则小波变换后的幅度值取决于前后码元的幅度、频率或相位大小。本文利用小波变换模极大值的方法来判别数字信号码元的跳变点,以此来引言0信号的奇异点往往包含有重要的信息,数字通信信号在码元边界上由于幅度、频率或相位的变化会产生奇异点,有效地判别出通信信号的码元跳变点可准确检测出信号的码速率。小波分析法可在空间局部上判别出信号的奇异点,通过计算相邻奇异点之间的最小间隔可估算出信号的码元符号率。O.Rioul等人将小波变换分析方法用于故障点的检测,国内也有赵犁丰、袁海英等人将此方法应用于故障点的检测。K.C.Ho,W.Prokopiw和Y.T.Chan将小波变换分析法用于数字通信信号的处理,他们是通过分析数字通信信号经过小波1数字信号的小波分析1.1小波变换原理小波变换的定义是把基本小波函数Ψ(t)做位移τ后,再在不同尺度下与待分析的信号做内积:收稿日期:2008-05-21+∞τ波如表1所示。表1符合条件的母小波1S(t)Ψ3(t-)dt,α>0(1)α∫-Ws(α,τ)=α式中:上标3表示复数共轭;基本小波(也叫母小波)函数Ψ(t)在实轴(-∞,+∞)上满足条件:(1)Ψ(t)的积分等于:+∞∫-∞Ψ(μ)=0(2)(2)Ψ(t)的均方积分等于:+∞∫-∞Ψ2(μ)=1(3)1.2基于小波变换的模极大值检测原理信号跳变点的位置有时是由小波变换的过零点反映的,有时是由其极值点反映的。一般地说根据过零点作检测不如根据极值点做检测。过零点易受噪声干扰,而且有时过零点反映的不是跳变点,而是信号在慢变区间的转折点。图1中函数θ(t)为高斯函数,与信号函数s(t)卷积得出图1中的第2个图形。其中高斯函数θ(t)的表达式为:由于前面3种小波系的母小波没有明确的解析表达式,本文选用解析表达式较为简单的Gaussian小波系的gaus2小波作为母小波。gaus2小波是21t(1-t2)e-Ψ(t)=(5)22π其图形如图2所示。21te-θ(t)=(4)22π图2gaus2小波函数图形1.3数字通信信号的码元跳变检测下面以二进制幅度键控(BASK)信号为例。对于BASK信号,载波幅度随着通信信号序列的变化而改变,其表达式可写为:SBASK(t)=B(t)cos(2πfct)式中:fc为载波频率;B(t)为一个二进制序列:(6)∑AnuTs(t-nTs)B(t)=(7)n式中:uT为单位幅度的矩形函数,其支撑区间为[0,图1极值检测与过零检测对比图sTs);Ts为信号的码元周期;fc取值为1;An取二进制数字0和1,且出现概率分别是p和1-p。BASK信号的小波变换表示为:可以看出,信号s(t)3θ(t)只有2个跳变点,分别在t1和t3时刻,过零检测出现3个过零点,其中t2时刻并不是信号的跳变点,其反映的是s(t)3θ(t)的转折点。因此过零检测存在误差,本文采用小波变换模极值点来检测数字通信信号码元的跳变点。要使极值检测有效,选取的母小波必须满足以下条件:首先,母小波应是某一...