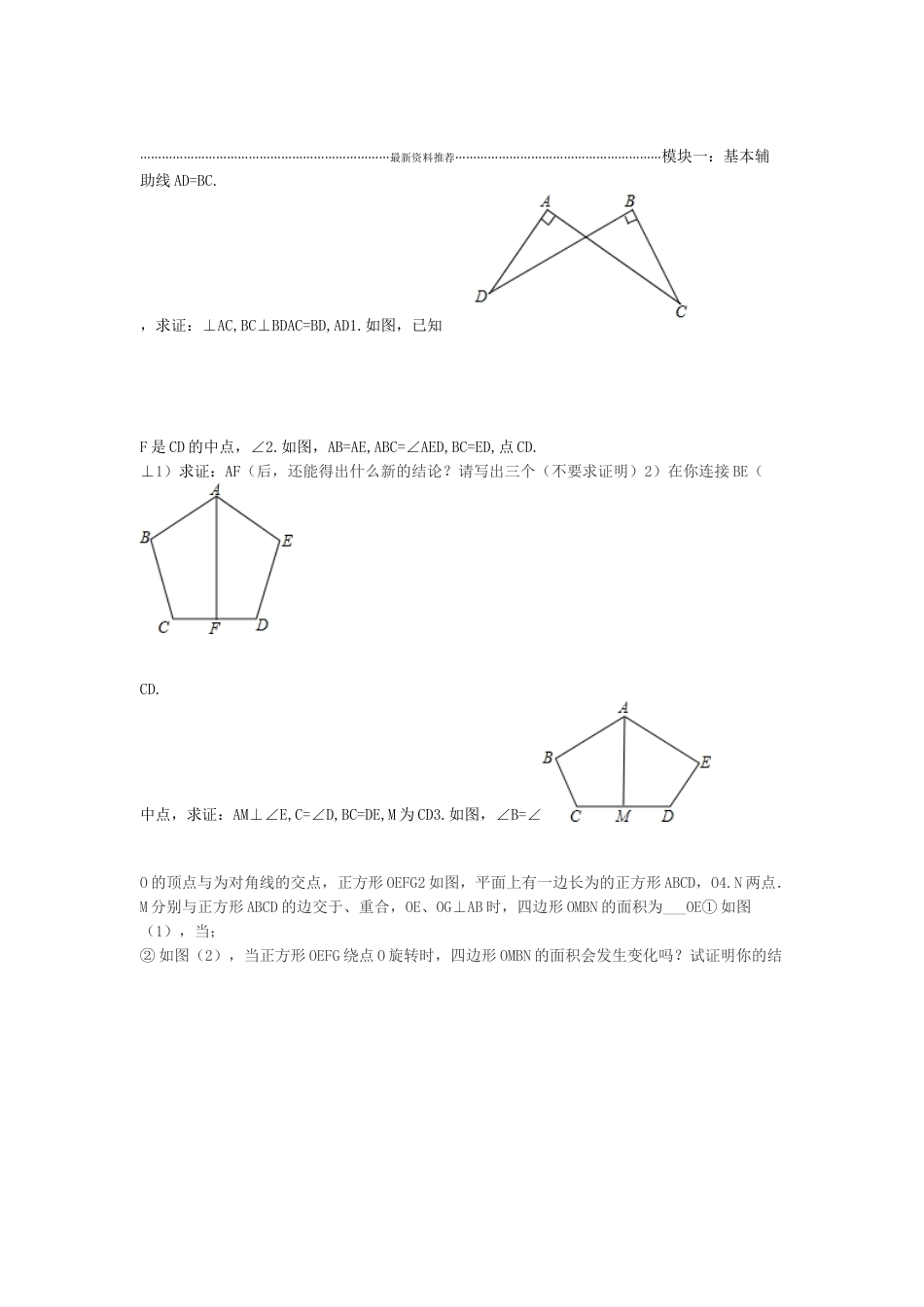
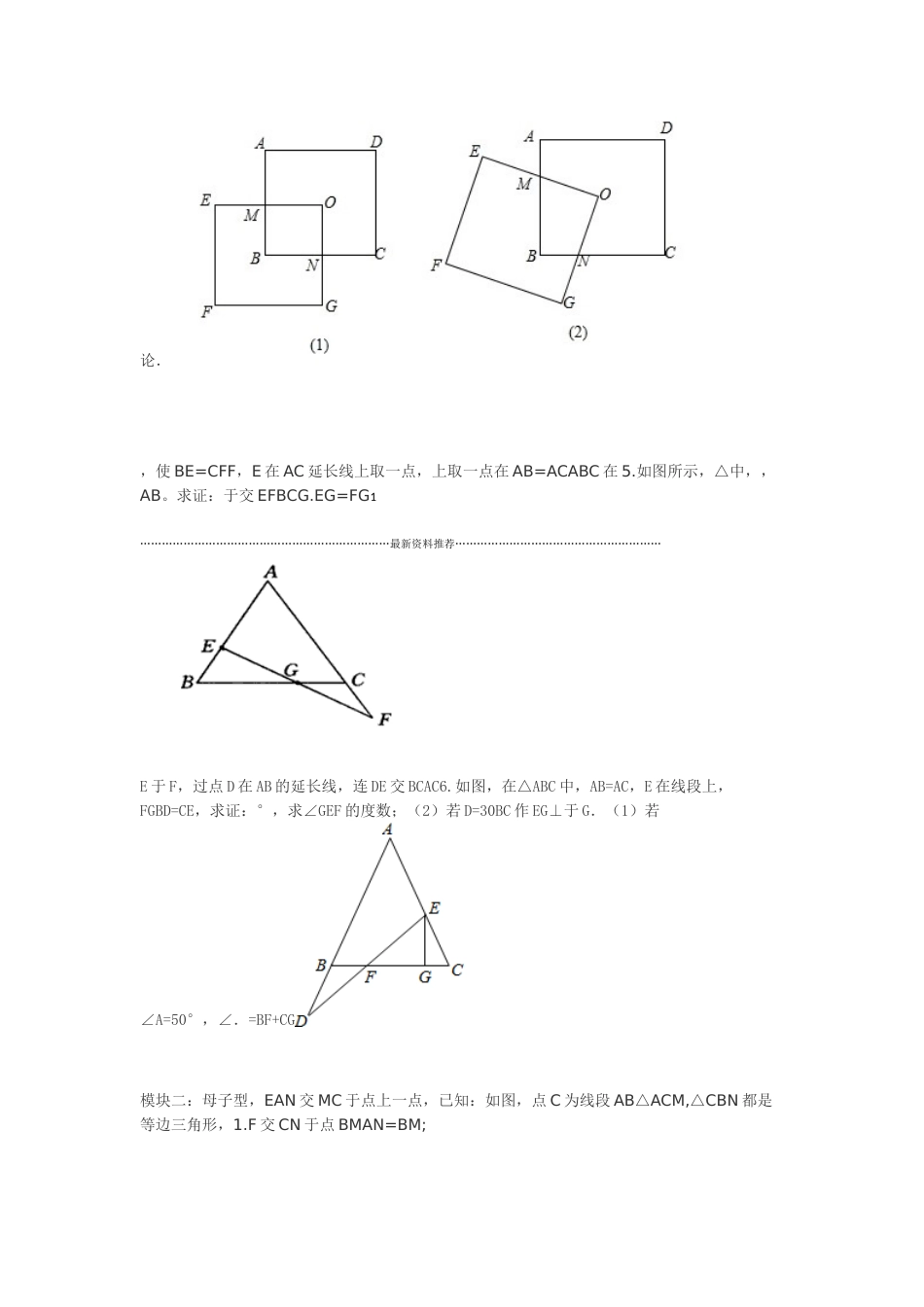
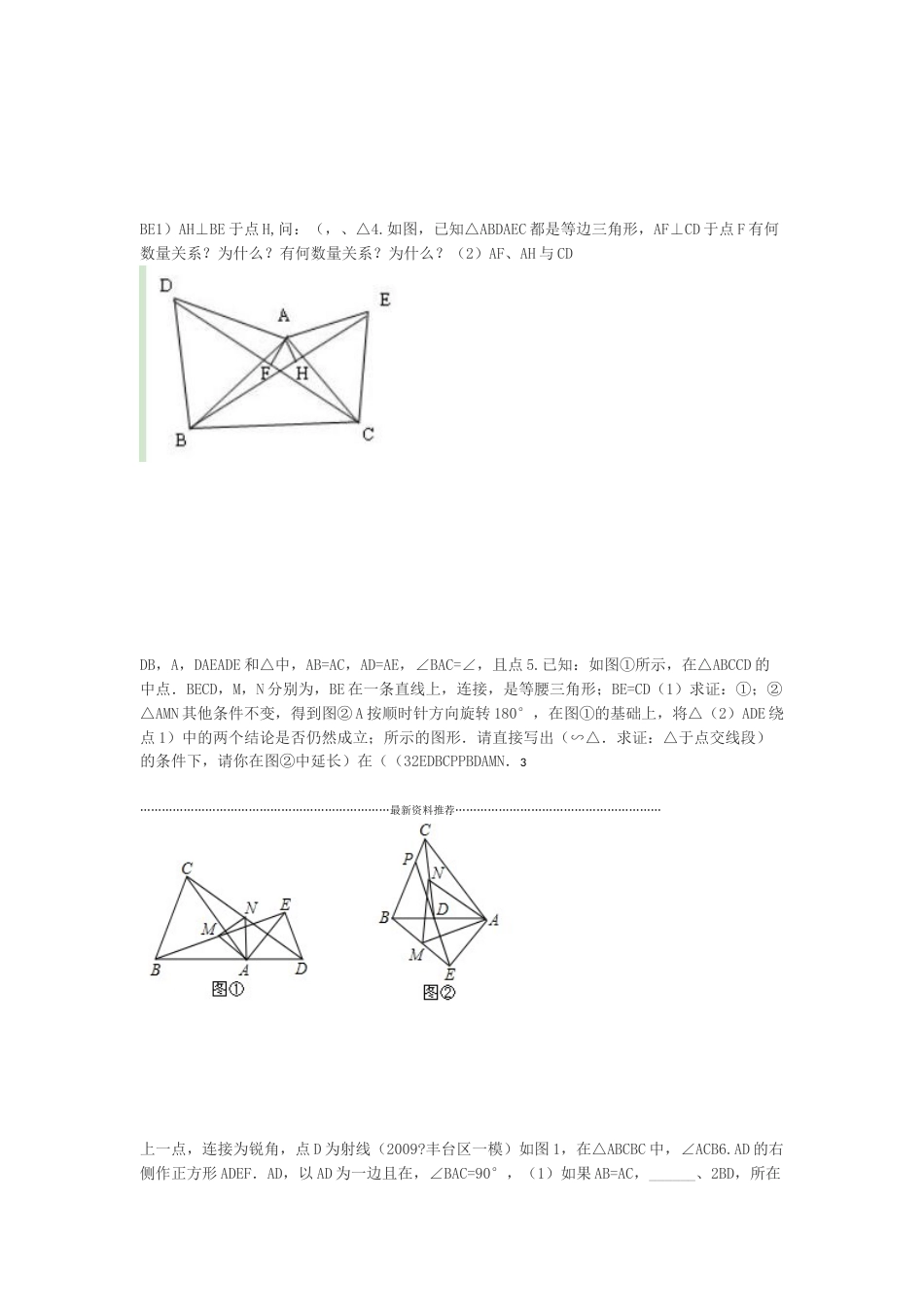
……………………………………………………………最新资料推荐…………………………………………………模块一：基本辅助线AD=BC.，求证：⊥AC,BC⊥BDAC=BD,AD1.如图，已知F是CD的中点，∠2.如图，AB=AE,ABC=∠AED,BC=ED,点CD.⊥1）求证：AF（后，还能得出什么新的结论？请写出三个（不要求证明）2）在你连接BE（CD.中点，求证：AM⊥∠E,C=∠D,BC=DE,M为CD3.如图，∠B=∠O的顶点与为对角线的交点，正方形OEFG2如图，平面上有一边长为的正方形ABCD，O4.N两点．M分别与正方形ABCD的边交于、重合，OE、OG⊥AB时，四边形OMBN的面积为___OE①如图（1），当；②如图（2），当正方形OEFG绕点O旋转时，四边形OMBN的面积会发生变化吗？试证明你的结论．，使BE=CFF，E在AC延长线上取一点，上取一点在AB=ACABC在5.如图所示，△中，，AB。求证：于交EFBCG.EG=FG1……………………………………………………………最新资料推荐…………………………………………………E于F，过点D在AB的延长线，连DE交BCAC6.如图，在△ABC中，AB=AC，E在线段上，FGBD=CE，求证：°，求∠GEF的度数；（2）若D=30BC作EG⊥于G．（1）若∠A=50°，∠．=BF+CG模块二：母子型，EAN交MC于点上一点，已知：如图，点C为线段AB△ACM,△CBN都是等边三角形，1.F交CN于点BMAN=BM;求证：(1)为等边三角形求证：△CEF(2)、AE中，∠EOF=90°，连结RtOAB如图，已知，等腰Rt△中，∠AOB=90°，等腰△EOF2.。BFAE2AE=BF1BF。求证：（）；（）⊥2……………………………………………………………最新资料推荐…………………………………………………；都是正方形，显然图中有AG=CE，AG⊥CE如图3.1，若四边形ABCD、四边形GFED是否成立？若成立，请给出证明；D旋转到如图2的位置时，AG=CE（1）当正方形GFED绕若不成立，请说明理由；．AD于MD旋转到如图3的位置时，延长CE交AG于H，交GFED（2）当正方形绕AG⊥CH；①求证：2时，求CH的长．②当AD=4，DG=BE1）AH⊥BE于点H,问：（，、△4.如图，已知△ABDAEC都是等边三角形，AF⊥CD于点F有何数量关系？为什么？有何数量关系？为什么？（2）AF、AH与CDDB，A，DAEADE和△中，AB=AC，AD=AE，∠BAC=∠，且点5.已知：如图①所示，在△ABCCD的中点．BECD，M，N分别为，BE在一条直线上，连接，是等腰三角形；BE=CD（1）求证：①；②△AMN其他条件不变，得到图②A按顺时针方向旋转180°，在图①的基础上，将△（2）ADE绕点1）中的两个结论是否仍然成立；所示的图形．请直接写出（∽△．求证：△于点交线段）的条件下，请你在图②中延长）在（（32EDBCPPBDAMN．3……………………………………………………………最新资料推荐…………………………………………………上一点，连接为锐角，点D为射线（2009?丰台区一模）如图1，在△ABCBC中，∠ACB6.AD的右侧作正方形ADEF．AD，以AD为一边且在，∠BAC=90°，（1）如果AB=AC，______、2BD，所在直线的位置关系为线段CF，①当点D在线段BC上时（与点B不重合）如图；的数量关系为______、线段CFBD，①中的结论是否仍然成立，并说明理由；的延长线上时，如图3②当点D在线段BC（点BC满足什么条件时，ACBCF⊥是锐角，BAC点D在线段BC上，当∠AC）（2如果AB≠，∠不重合），并说明理由．C、F倍长中线模块三）倍长类中线）倍长中线（2（1AB=AC．，求证：，且平分∠中，已知：如图，△1.ABCADBACBD=CD4……………………………………………………………最新资料推荐…………………………………………………11AC>AB,AM＜(AB+AC)．AC-AB2.已知，如图△ABC中，AM是BC边上的中线，求证：（）＜22:EF//求证BD,AD上，DE=CD,EF=AC,BAC,E,F3.如图所示，已知△ABC中，AD平分∠分别在AB.EF．求证：、AC上，且DE⊥DFBE+CF＞分别在的中线，4.AD如图，是△ABCE、FAB4.求．，BD=AB连接CDDCEAB=AC，边上的中线，是AB延长AB到，使已知在△如图，ABC中，1CD.CE=证：2证明：直角三角形斜边上的中线等于斜边上的一半。5.5……………………………………………………………最新资料推荐…………………………………………………的ABDE7.分别以△ABC的边AB,AC为边，向三角形的外侧作正方形和正方...