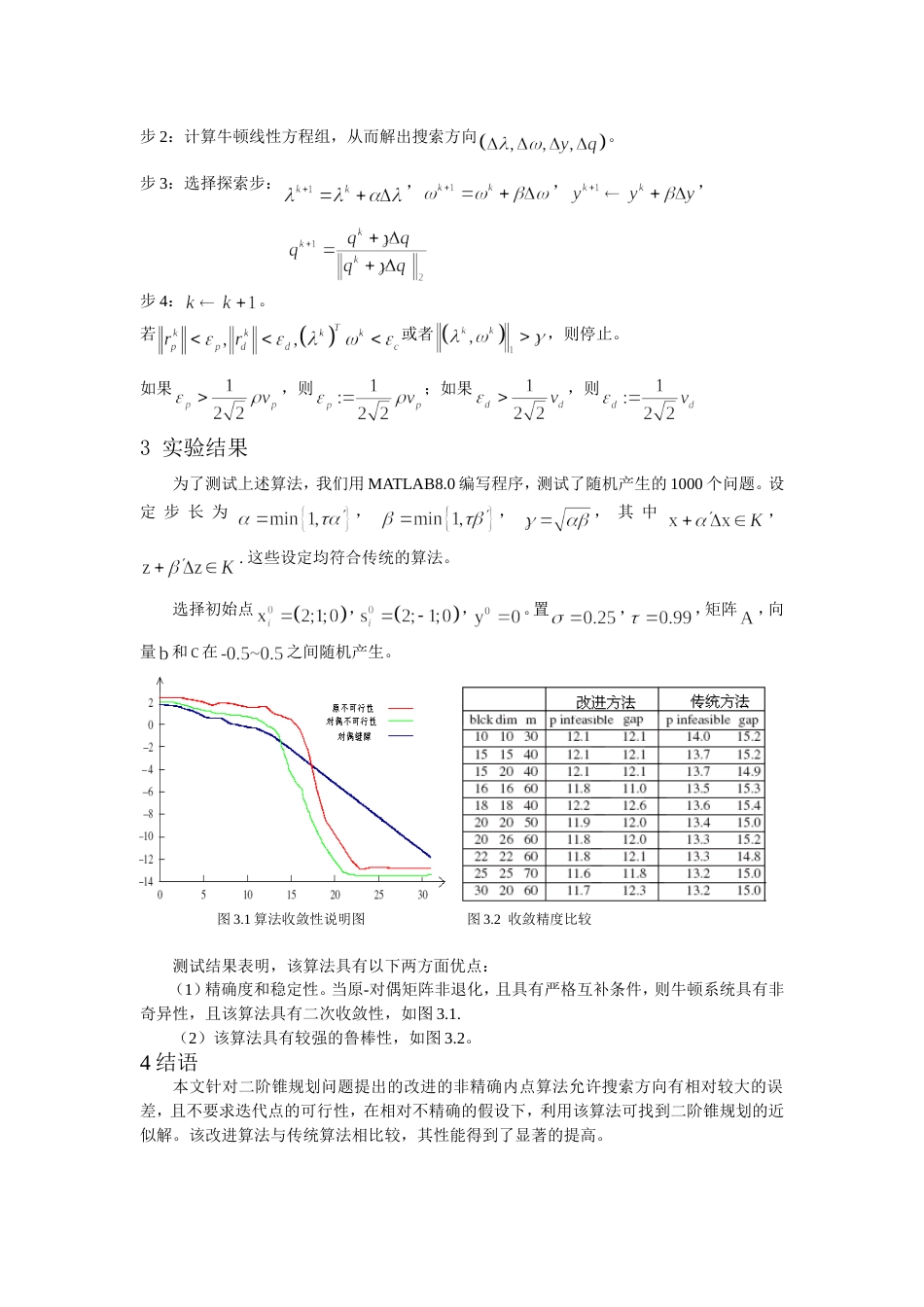
应用改进的内点法求二阶锥规划的最优解王璐1,高雷阜1（1辽宁工程技术大学数学与系统科学研究所,辽宁阜新123000)摘要：本文针对二阶锥规划的优化问题提出了一种改进的非精确内点算法。本算法允许搜索方向有相对较大的误差，且不要求迭代点的可行性，在相对不精确的假设下，利用该算法可找到二阶锥规划的近似解。从实验的结果可以看出,改进算法的性能得到了显著的提高。关键词：二阶锥规划；非精确搜索方向；内点算法中图分类号：O232文献标识码：AAnApplicationofImprovedinteriorpointalgorithmonsecond-orderconeprogrammingWangLu1,GaoLei–fu1(1.MathematicsandSystemsScienceInstituteofLiaoningTechnologyUniversityLiaoningFuxin123000)Abstract:Ainexactinteriorpointalgorithmispresentedforsolvingthesecond-orderconeprogramming(SOCP)problem.Thesearchdirectionofthisalgorithmallowsarelativelylargererroranddosenotrequireinterationpointstobewithinthesetsofstrictlyfeasiblesolutions,undermildassumptionsontheinexactness,wecanfindanapproximatesolutionoftheSOCPbyusingthisalgorithm.Numericalresultssuggesttheeffectivenessofourproposedalgorithm.Keywords:second-orderconeprogramming;inexactsearchdirection;interiorpointalgorithm0引言二阶锥规划问题是一族凸优化问题，而非线性规划，它是半定规划的特例。人们对二阶锥规划的研究已经有很长的历史了，如经典的Fermat-Weber问题可追溯到几个世纪以前,由于把二阶锥规划转化成半定规划求解，其效果并不很理想，因此人们开始对二阶锥规划进行深入研究。对二阶锥规划的研究主要是建立在欧几里得约当代数基础上的，Faruat和Konary详细论述了这一理论。随后Nesetorv和Nemiorvski提出了用内点法求解凸规划的理论。上世纪九十年代，人们开始用内点法求解二阶锥规划及其特例(凸二约束下的二次规划)，自Nesteorv和Todd第一次用多项式时间原-对偶路径跟踪法以来，求解二阶锥规划的原-对偶内点算法才得以长足发展。目前，对于二阶锥规划算法与性质的研究以及其在各领域的广泛应用都有了较大的进展，本文将对二阶锥规划的内点算法做进一步的研究。基于文献[3]中半定规划的算法，提出了一种新的改进的非精确内点算法。1相关概念定义1二阶锥及其规划二阶锥定义为：，为二阶锥的维数.其原规划为：对偶规划为：，其中。定义2欧几里得约当代数二阶锥规划的算法是基于约当代数发展起来的，与二阶锥相伴的欧几里得约当代数定义为：，其中。令，则有，其中定义3向量的谱分解,从而被写成，其中，，，将分成块处理,其中,则，,,,定义4约当块的标准化定义标准约当块,其中标准特征向量，将约当块转化为约当块，通过下面式子：，详见文献[4]。因此,2非精确内点算法2.1主要思想内点算法是一类求解二阶锥规划的非常有效的方法,在内点算法的每一步迭代中主要工作是通过求解一个非线性方程组来找一个搜索方向，但是由于计算机的精度原因，由以前的方法直接求解不仅花费了大量计算时间，而且得不到真正精确的搜索方向.事实上，非精确内点算法的基本思想是在中心路径的邻域内围绕中心路经前进，最终趋向最优点，但在计算过程中约当矩阵会出现奇异的现象,导致算法不稳定。本文提出的算法是将约当块通过函数进行标准化处理，再利用非精确内点算法求解二阶锥规划的最优解，这样既可保证算法的稳定性，又可以保证算法的全局收敛性，节约了大量的计算时间，使算法变得更为有效.互补松弛定理：如果是二阶锥原规划的最优解，是其对偶规划的最优解，那么。基于互补松弛定理，谱分解定义及约当块的标准化的相关理论,二阶锥规划可转化为:2.2中心路径及其邻域探索步：，，，牛顿线性方程组：2.3非精确内点算法的实现假设：（1）是二阶锥规划的原-对偶可行解，是特征值。（2），其中选择，初始点，选择，这样使得。步1：选择步2：计算牛顿线性方程组，从而解出搜索方向。步3：选择探索步：，，，步4：。若或者，则停止。如果，则；如果，则3实验结果为了测试上述算法，我们用MATLAB8.0编写程序，测试了随机产生的1000个问题。设定步长为，，，其中...