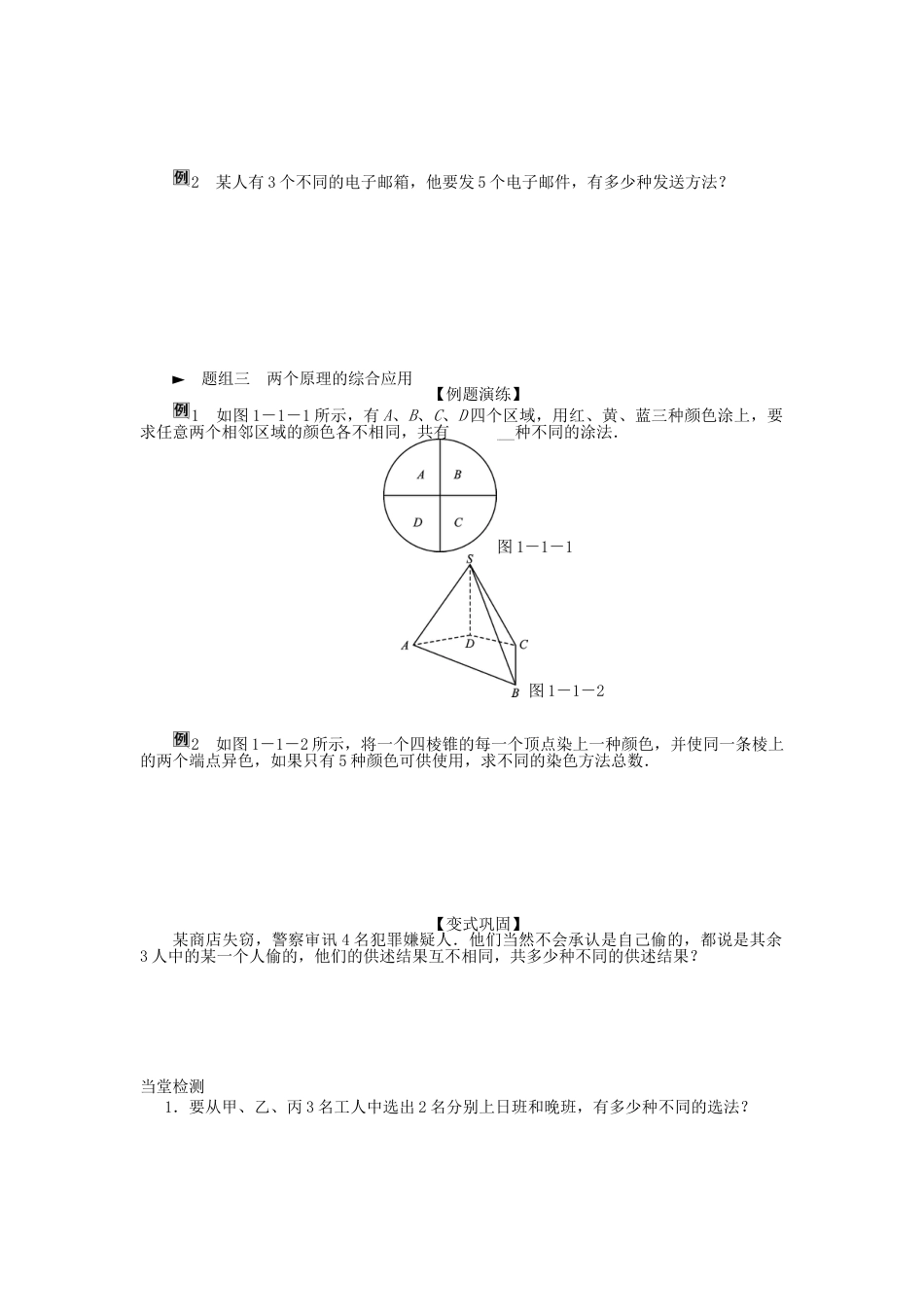
1．1分类加法计数原理与分步乘法计数原理第1课时加法原理与乘法原理(一)学习目标：（1）理解分类计数原理与分步计数原理（2）会利用两个原理分析和解决一些简单的应用问题购买福利彩票可以从当地投注站购买，也可以电话投注．如果张三想购买一注福利彩票，他可以有几种购买方式？►知识点一分类加法计数原理的解读完成一件事有________不同方案，在第1类方案中有______种不同的方法，在第2类方案中有______种不同的方法，那么完成这件事共有N＝________种不同的方法．►知识点二分步乘法计数原理的解读完成一件事需要________步骤，做第1步有____种不同的方法，做第2步有____种不同的方法，那么完成这件事共有N＝__________种不同的方法．►题组一分类计数原理的应用【例题演练】1某一数学问题可用综合法和分析法两种方法证明，有5位同学只会用综合法证明，有3位同学只会用分析法证明，现任选1名同学证明这个问题，不同的选法种数为________种．2一个信箱中有15封信，另一个信箱中有5封信，每封信的内容均不相同，从两个信箱中任取一封信，有多少种不同的取法？►题组二分步计数原理的应用【例题演练】1将1,2,3填入3×3的方格中，要求每行、每列都没有重复数字，下面是一种填法，则不同的填写方法共有()123312231A．6种B．12种C．24种D．48种2某人有3个不同的电子邮箱，他要发5个电子邮件，有多少种发送方法？►题组三两个原理的综合应用【例题演练】1如图1－1－1所示，有A、B、C、D四个区域，用红、黄、蓝三种颜色涂上，要求任意两个相邻区域的颜色各不相同，共有________种不同的涂法．图1－1－1图1－1－22如图1－1－2所示，将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱上的两个端点异色，如果只有5种颜色可供使用，求不同的染色方法总数．【变式巩固】某商店失窃，警察审讯4名犯罪嫌疑人．他们当然不会承认是自己偷的，都说是其余3人中的某一个人偷的，他们的供述结果互不相同，共多少种不同的供述结果？当堂检测1．要从甲、乙、丙3名工人中选出2名分别上日班和晚班，有多少种不同的选法？2．若分给你10块完全一样的糖，规定每天至少吃一块，每天吃的块数不限，问共有多少种不同的吃法？n块糖呢？第2课时加法原理与乘法原理(二)学习目标：会利用两个原理分析和解决一些简单的应用问题一个口袋内装有5个小球，另一个口袋内装有4个小球，所有这些小球的颜色互不相同．(1)从两个口袋内任取一个小球，有多少种不同的取法？(2)从两个口袋内各取一个小球，有多少种不同的取法？►知识点分类加法计数原理与分步乘法计数原理的联系与区别1．分类加法计数原理与分步乘法计数原理，回答的都是有关做一件事的______________的问题．2．区别在于：分类加法计数原理针对的是________问题，其中各种方法相互独立，用其中任何一种方法都可以做完这件事；分步乘法计数原理针对的是________问题，各个步骤中的方法相互依存，只有各个步骤都完成才算做完这件事．►题组一运用两个原理解决含有限制条件的实际问题【例题演练】1若x，y∈N*，且x＋y≤6，则有序自然数对(x，y)的个数为()A．6B．8C．10D．152已知集合A＝{a1，a2，a3，a4}，集合B＝{b1，b2}，其中ai，bj(i＝1,2,3,4，j＝1,2)均为实数．(1)从集合A到集合B能构成多少个不同的映射？(2)能构成多少个以集合A为定义域，集合B为值域的不同的函数？►题组二两个基本原理思想的灵活运用【例题演练】1将3种作物种植在如图1－1－3所示的5块试验田里，每块种植一种作物且相邻的试验田不能种植同一作物，不同的种植方法共有________种．(以数字作答)图1－1－32同室4人各写1张贺年卡，先集中起来，然后每人从中各拿1张别人送出的贺年卡，则4张贺年卡不同的分配方式有多少种？【变式巩固】从0,1,2,3,4,5,6中任意取出三个不同的数字作为二次函数y＝ax2＋bx＋c的系数，可有多少个不同的二次函数的表达式？其中二次函数对应的曲线关于y轴对称的有多少个？当堂检测1．在1～20共20个整数中取两个数相加,使其和为偶数的不同取法共有多少种?2.如图一,要给①,②,③,④四块区域分别涂上五种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同...