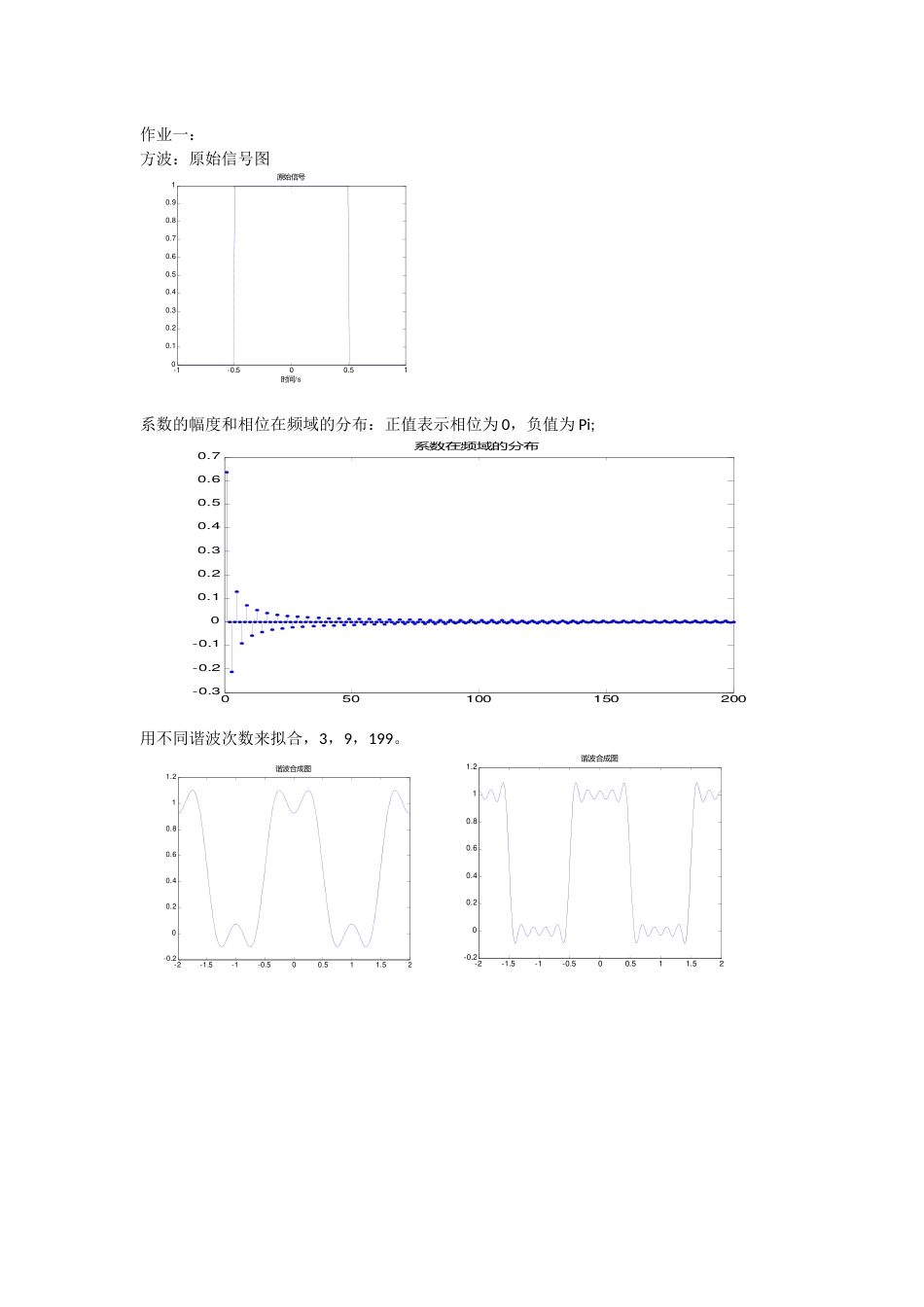
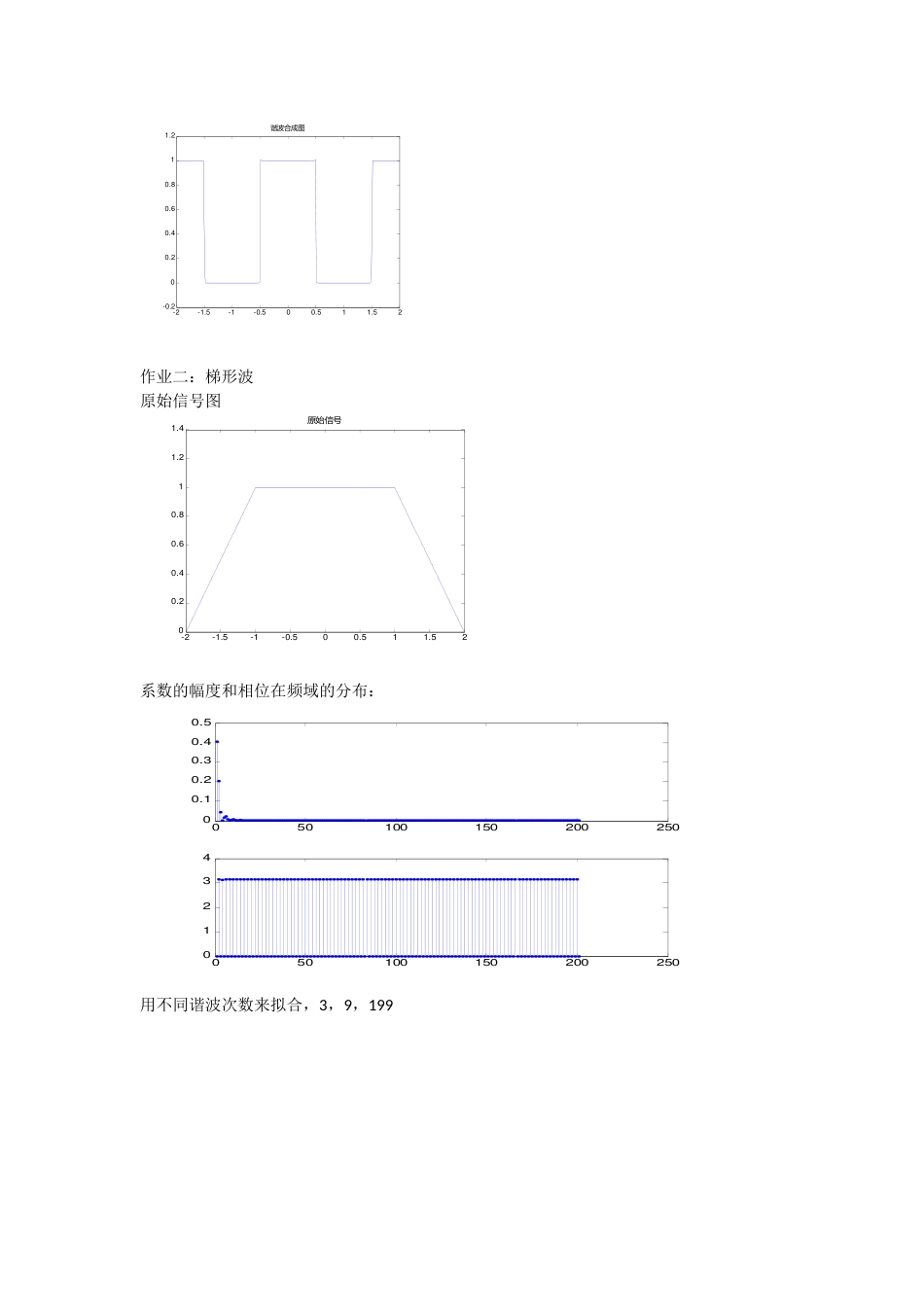
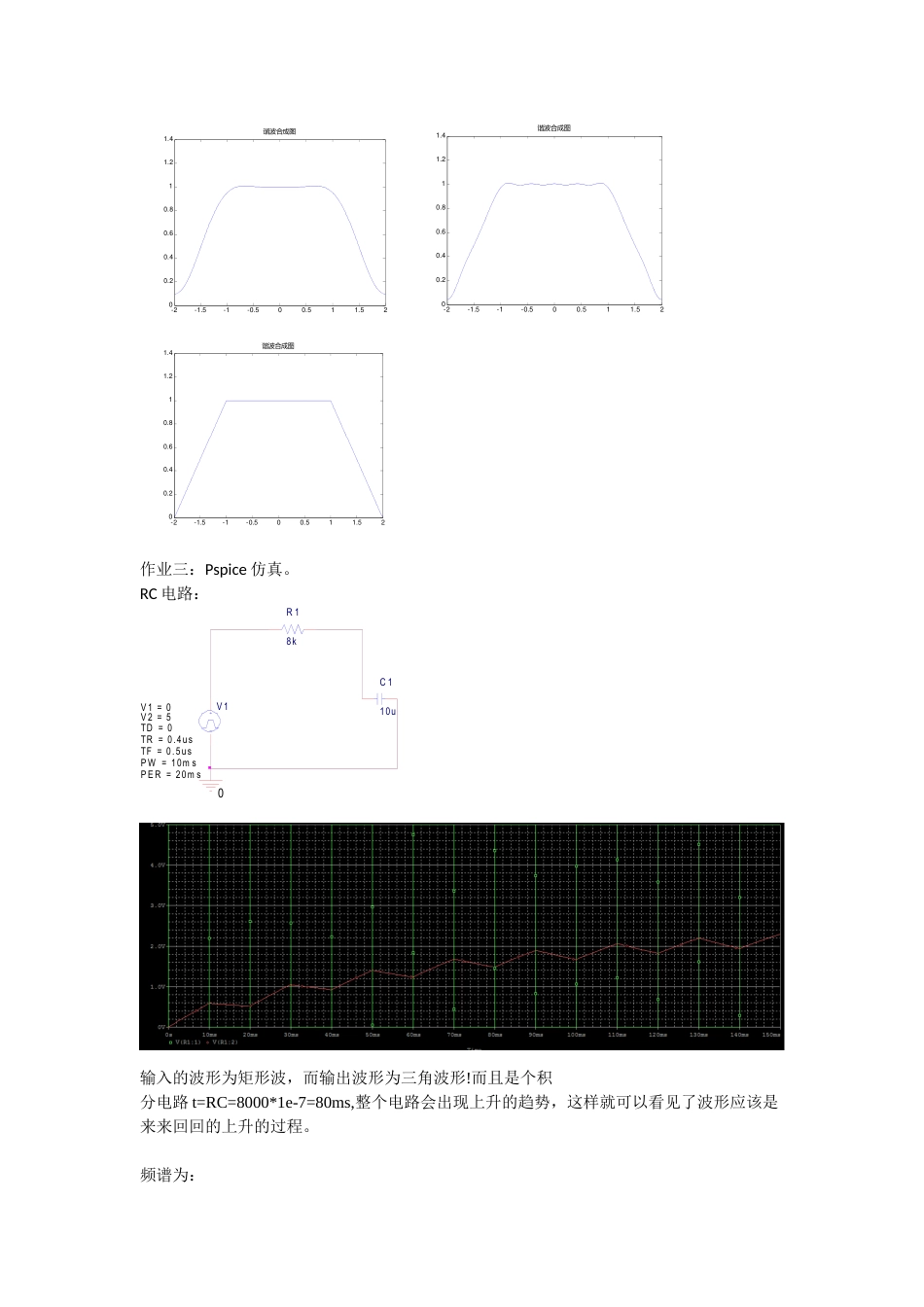
作业一:方波:原始信号图-1-0.500.5100.10.20.30.40.50.60.70.80.91/s时间原始信号系数的幅度和相位在频域的分布:正值表示相位为0,负值为Pi;050100150200-0.3-0.2-0.100.10.20.30.40.50.60.7系数在频域的分布用不同谐波次数来拟合,3,9,199。-2-1.5-1-0.500.511.52-0.200.20.40.60.811.2谐波合成图-2-1.5-1-0.500.511.52-0.200.20.40.60.811.2谐波合成图-2-1.5-1-0.500.511.52-0.200.20.40.60.811.2谐波合成图作业二:梯形波原始信号图-2-1.5-1-0.500.511.5200.20.40.60.811.21.4原始信号系数的幅度和相位在频域的分布:05010015020025000.10.20.30.40.505010015020025001234用不同谐波次数来拟合,3,9,199-2-1.5-1-0.500.511.5200.20.40.60.811.21.4谐波合成图-2-1.5-1-0.500.511.5200.20.40.60.811.21.4谐波合成图-2-1.5-1-0.500.511.5200.20.40.60.811.21.4谐波合成图作业三:Pspice仿真。RC电路:V1TD=0TF=0.5usPW=10msPER=20msV1=0TR=0.4usV2=5R18kC110u0V00V0V输入的波形为矩形波,而输出波形为三角波形!而且是个积分电路t=RC=8000*1e-7=80ms,整个电路会出现上升的趋势,这样就可以看见了波形应该是来来回回的上升的过程。频谱为:附录:%方波m文件clearall;closeall;T=2,tao=1;N=200;t=linspace(-T/2,T/2,N);forn=1:Nif(t(n)>=-0.5t(n)<=0.5),x(n)=1;elsex(n)=0;endendfigure(1);plot(t,x);holdon;xlabel('时间/s');title('原始信号');a=zeros(1,N);fork=1:Na(k)=2/(k*pi)*sin(k*pi/2);endfigure(2);stem((1:N),a,'.');title('系数在频域的分布');m=input('输入最大谐波阶数');f=zeros(1,N);f=0.5delf=0;fork=1:mdelf=delf+a(k).*cos(k*pi*t);endf=f+delf;figure(3);plot(t,f);title('谐波合成图');%n=[1:N]%a3=2/T*quadv(@(x)cos(2*pi/T.*n*x),-0.5,0.5);%矩形波m文件T=4;t=linspace(-T/2,T/2,201);N=201;fori=1:201ift(i)<=-1ft(i)=t(i)+2;elseift(i)>=1ft(i)=2-t(i);elseft(i)=1;endendfigure(1);plot(t,ft);title('原始信号');axis([-2201.4]);n=[1:N];a0=1/T*(quad(@(x)(x+2),-2,-1)+quad(@(x)(x-x+1),-1,1)+quad(@(x)(2-x),1,2));a=2/T*((quadv(@(x)(x+2).*cos(2*pi/T.*n*x),-2,-1))+(quadv(@(x)(x-x+1).*cos(2*pi/T.*n*x),-1,1))+(quadv(@(x)(2-x).*cos(2*pi/T.*n*x),1,2)));b=2/T*((quadv(@(x)(x+2).*sin(2*pi/T.*n*x),-2,-1))+(quadv(@(x)(x-x+1).*sin(2*pi/T.*n*x),-1,1))+(quadv(@(x)(2-x).*sin(2*pi/T.*n*x),1,2)));%f=a0+a(1)*cos(2*pi/T*t)+b(1)*sin(2*pi/T*t)+a(2)*cos(2*pi/T*t*2)+b(2)*sin(2*pi/T*t*2)+a(3)*cos(2*pi/T*t*3)+b(3)*sin(2*pi/T*t*3)%plot(t,f);c=sqrt(a.^2+b.^2);fai=acos(a./c);figure(2);subplot(2,1,1);stem(n,c,'.');subplot(2,1,2);stem(n,fai,'.');m=input('输入最大谐波阶数');f=zeros(1,N);f=a0;delf=0;fork=1:mdelf=delf+a(k).*cos(k*2*pi/T*t)+b(k)*sin(k*2*pi/T*t)endf=f+delf;figure(3);plot(t,f);title('谐波合成图');