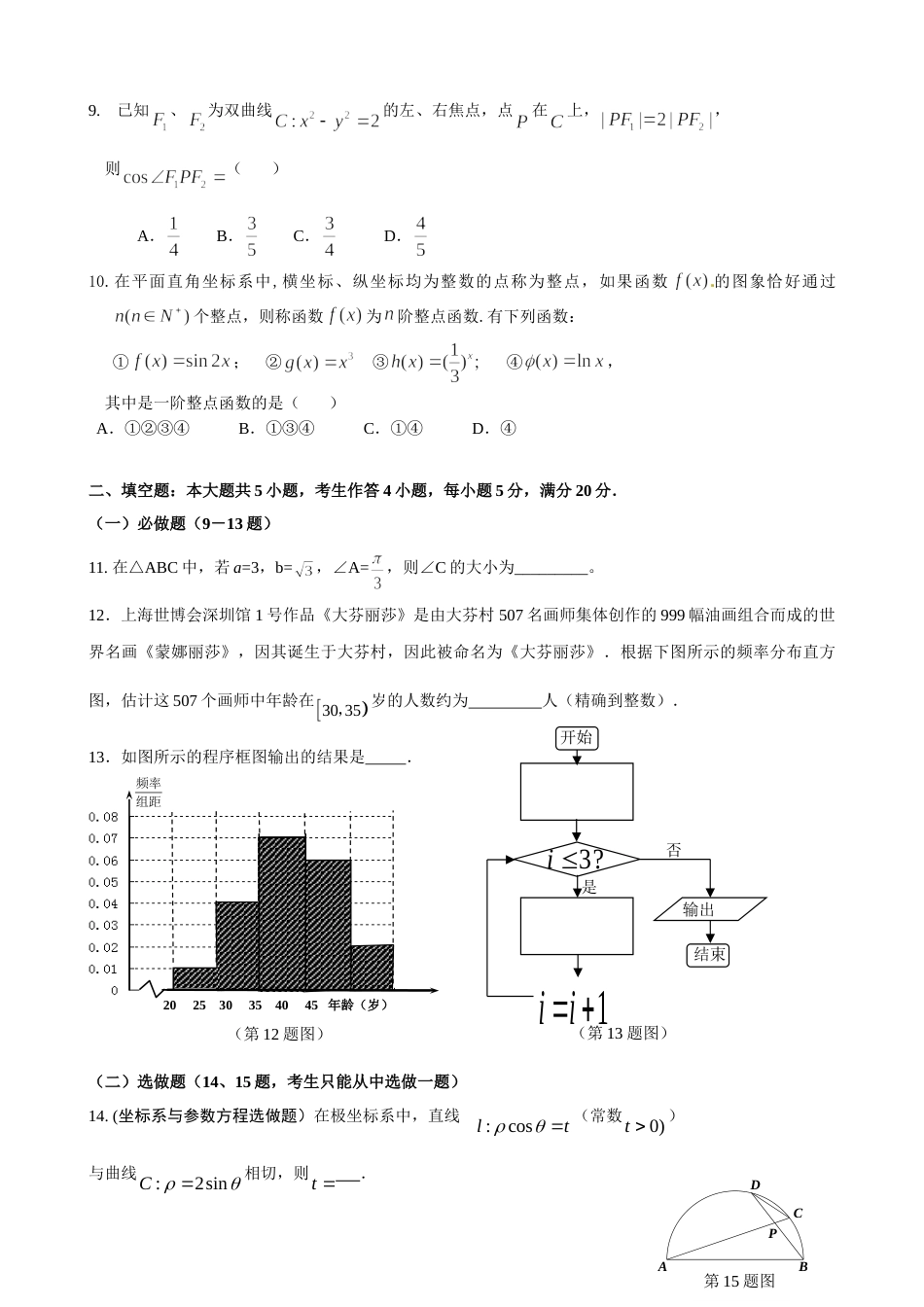
东莞中学松山湖学校高三三模测验数学(文科）一、选择题（本大题共10小题，每小题5分，满分50分.每小题给出的四个选项中，只有一项是符合题目要求.）1．已知全集，集合，，则（）A．{1,2,4}B．{2,3,4}C．{0,2,4}D．{0,2,3,4}2．函数的定义域是（）A．B．C．D．3．复数满足，则（）A．B．C．D．4．设，向量且，则（）A．B．C．D．5．如图，一个简单空间几何体的三视图其主视图与侧视图都是边长为2的正三角形，俯视图为正方形，则此几何体的表面积是（）A．B．12C．D．86．设，则“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件7.若，满足约束条件，则的最小值是（）A．-3B．0C．D．38．方程223xx的实数解的个数为（）A．2B．3C．1D．4俯视图主视图侧视图9.已知、为双曲线的左、右焦点，点在上，，则（）A．B．C．D．10.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点，如果函数的图象恰好通过个整点，则称函数为阶整点函数.有下列函数：①；②③④，其中是一阶整点函数的是（）A．①②③④B．①③④C．①④D．④二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（9－13题）11.在△ABC中，若a=3，b=，∠A=，则∠C的大小为_________。12．上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．根据下图所示的频率分布直方图，估计这507个画师中年龄在3035，岁的人数约为人（精确到整数）．13．如图所示的程序框图输出的结果是．（二）选做题（14、15题，考生只能从中选做一题）14.(坐标系与参数方程选做题）在极坐标系中，直线:coslt（常数t0)）与曲线:2sinC相切，则t．PDCBA第15题图（第12题图）频率组距202530354045年龄（岁）输出结束开始3?i1ii是否（第13题图）15．（几何证明选讲选做题）如图，AB是半圆的直径，弦AC和弦BD相交于点P，且3ABDC，则sinAPD．三、解答题：本大题共6小题，满分80分．解答应写出文字说明、证明过程或演算步骤16．(本小题满分12分)已知5sin5，(0,2)，1tan3．(1)求tan值；(2)求tan2的值．17．(本小题满分12分)某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：序号1234567891011121314151617181920数学成绩9575809492656784987167936478779057837283物理成绩9063728791715882938177824885699161847886若单科成绩85分以上（含85分），则该科成绩为优秀．（1）根据上表完成下面的22列联表（单位：人）：（2）根据题（1）中表格的数据计算，有多大的把握，认为学生的数学成绩与物理成绩之间有关系？（3）若从这20个人中抽出1人来了解有关情况，求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率．参考数据：随机变量22nadbcKabcdacbd，其中nabcd为样本容量；②独立检验随机变量2K的临界值参考表：数学成绩优秀数学成绩不优秀合计物理成绩优秀物理成绩不优秀合计20PK2ok0.500.400.250.150.100.050.0250.0100.0050.001ok0.4550.7081.3232.0722.7063.8415.0246.6357.87910.82818.（本题满分14分）如图所示，圆柱的高为2,是圆柱的母线，为矩形,,分别是线段的中点。（1）求证：平面平面；（2）求证：面；（3）求三棱堆的体积.19（本题满分14分）设数列的前项和为，且，为等差数列，且，．(1)求数列和通项公式；(2)设，求数列的前项和．20.（本题满分14分）已知动点P到定点2,0F的距离与点P到定直线l：x22的距离之比为22．（1）求动点P的轨迹C的方程；（2）设M、N是直线l上的两个点，点E与点F关于原点O对称，若EMFN0�,求MN的最小值.21.（本题满分14分）已知函数2()(1)ln1fxaxax.（1）讨论函数()fx的单调性；（2）设a2，证明：对任意1,2(0,)xx，1212|()()|4||fxfxxx.