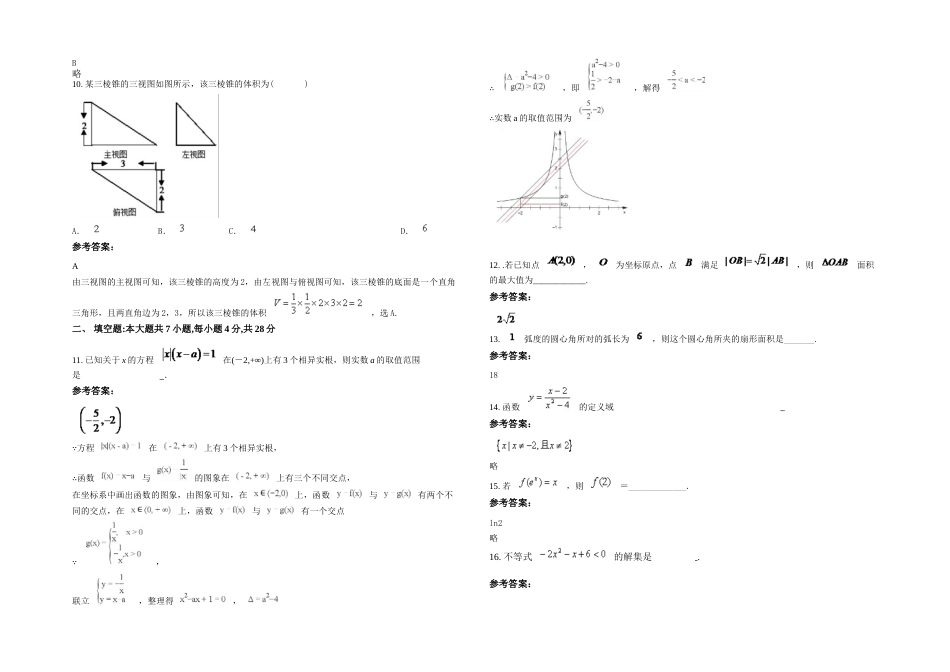
广东省深圳市光明中学2020年高一数学理联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有是一个符合题目要求的1.某几何体的三视图如图所示，则该几何体的体积为(）A．B．C．D．参考答案：A2.如图，三棱柱A1B1C1—ABC中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列叙述正确的是()．A、AE、B1C1为异面直线，且AE⊥B1C1B、AC⊥平面A1B1BAC、CC1与B1E是异面直线D、A1C1∥平面AB1E参考答案：A3.（5分）函数f（x）=|x|﹣cosx在（﹣∞，+∞）内（）A．没有零点B．有且仅有一个零点C．有且仅有两个零点D．有无究多个零点参考答案：C考点：函数的零点．专题：函数的性质及应用．分析：函数f（x）=|x|﹣cosx的零点个数可转化为函数y=|x|与y=cosx的图象交点的个数．结合它们的图象特征即可作出判断．解答：函数f（x）=|x|﹣cosx的零点个数，即方程|x|﹣cosx=0的根的个数，也即函数y=|x|与y=cosx的图象交点的个数．当0≤x≤时，y=|x|=x从0递增到，y=cosx从1递减到0，所以两函数图象在上只有一个交点，当x＞时，y=|x|=x＞＞1，y=cosx≤1，所以两函数图象在（，+∞）上没有交点，所以y=|x|与y=cosx的图象在上也只有一个交点，综上，函数y=|x|与y=cosx的图象交点的个数是2，故函数f（x）=|x|﹣cosx的零点个数为2．故选C．点评：本题考查函数的零点问题，即相应方程根的问题，注意体会转化思想与数形结合思想在本题中的运用．4.已知直线平行，则实数的值是（）参考答案：C略5.若样本1+x1，1+x2，1+x3，…，1+xn的平均数是10，方差为2，则对于样本2+x1，2+x2，…，2+xn，下列结论正确的是（）A．平均数为10，方差为2B．平均数为11，方差为3C．平均数为11，方差为2D．平均数为12，方差为4参考答案：C6.如图，已知B、C是以原点O为圆心，半径为1的圆与x轴的交点，点A在劣弧（包含端点）上运动，其中，，作于H．若记，则的取值范围是（A）（B）（C）（D）参考答案：C略7.函数y=的图象可能是()A．B．C．D．参考答案：B【考点】函数的图象．【专题】函数的性质及应用．【分析】当x＞0时，，当x＜0时，，作出函数图象为B．【解答】解：函数y=的定义域为（﹣∞，0）∪（0，+∞）关于原点对称．当x＞0时，，当x＜0时，，此时函数图象与当x＞0时函数的图象关于原点对称．故选B【点评】本题考查了函数奇偶性的概念、判断及性质，考查了分段函数的图象及图象变换的能力．8.函数的图象可能是（）参考答案：D略9.已知集合A={-1,0,1},B={x︱-1≤x＜1},则A∩B=()（A）{0}（B）{0，-1}（C）{0，1}（D）{0，1，-1}参考答案：B略10.某三棱锥的三视图如图所示，该三棱锥的体积为()A．B．C．D．参考答案：A由三视图的主视图可知，该三棱锥的高度为2，由左视图与俯视图可知，该三棱锥的底面是一个直角三角形，且两直角边为2，3，所以该三棱锥的体积，选A.二、填空题:本大题共7小题,每小题4分,共28分11.已知关于x的方程在(－2,+∞)上有3个相异实根，则实数a的取值范围是．参考答案： 方程在上有3个相异实根，∴函数与的图象在上有三个不同交点，在坐标系中画出函数的图象，由图象可知，在上，函数与有两个不同的交点，在上，函数与有一个交点 ，联立，整理得，∴，即，解得∴实数a的取值范围为12..若已知点，为坐标原点，点满足，则面积的最大值为____________.参考答案：13.弧度的圆心角所对的弧长为，则这个圆心角所夹的扇形面积是_______.参考答案：1814.函数的定义域参考答案：略15.若，则＝_____________．参考答案：ln2略16.不等式的解集是.参考答案：(-)()17.已知a、b是两非零向量,且a与b不共线,若非零向量c与a共线,则c与b必定_____参考答案：不共线三、解答题：本大题共5小题，共72分。解答应写出文字说明，证明过程或演算步骤18.已知:是定义在区间上的奇函数,且.若对于任意的时,都有．（1）解不等式．（2）若对所有恒成立,求实数的取值范围参考答案：(1)令则有，即.当时,必有在区间上是增函数解之所求解集为(2)在区间上是增函数,又对于所有,恒成立,即在时恒成立记,则有即解之得,或或的取值范围是19.已知函数.（1）若f(－1）＝f(1)，求a，...