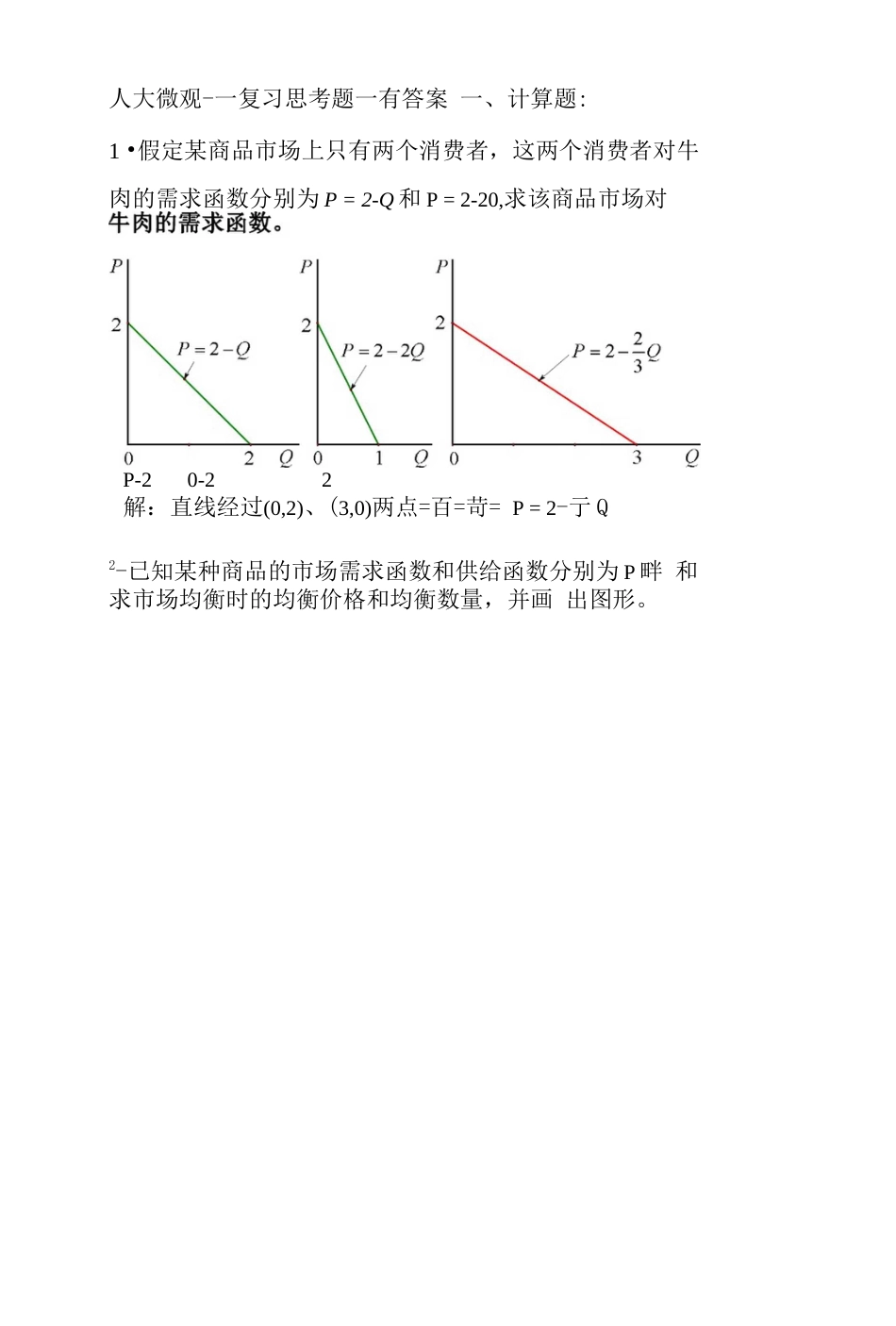
人大微观-一复习思考题一有答案一、计算题:1•假定某商品市场上只有两个消费者，这两个消费者对牛肉的需求函数分别为P=2-Q和P=2-20,求该商品市场对P-20-22解：直线经过(0,2)、(3,0)两点=百=苛=P=2-亍Q2-已知某种商品的市场需求函数和供给函数分别为P畔和求市场均衡时的均衡价格和均衡数量，并画出图形。M：p=—Q心02+53O5~=>23+250-250=0=>(e-5)-(e2+5o+5o)0>030?+50+50>0n0=5,P=l().603.已知某一商品的市场需求函数为e=IOO-4P,求P=10时的需求价格弹性系数。解：p=10,0=60,塑=-4,~dPPd()10/八2=>幺=-------=------(一4)=—“OdP60v734•某人对消费品x的需求函数为：p=\oo-4q,分别计算价格P二60和0=900时的需求价格弹性系数。解：P=60.2=(100-60)2=1600PdOP1P1〉w------------—------------•-----------------------------------♦-------------------------------------♦---------------------------------OdP~Q叮O_1p-o.5dO2幺1600_1x1600-o.52运用同样方法：当Q=900时，ed=4.71二35•已知某商品的需求函数为：P=1求该需求函数上任一PdOP=>----------------=---------QdPQ1p1do点的价格弹性系数。解：假设任意一点的坐标为（0,人）十崔76.下图中三条需求曲线分别为直线AB、AC、AD.（1）比较a、b、c三点的价格弹性系数的大小比较a、h、k三点的价格弹性系数的大小答案:&/创七严电=零7.若某人的效用函数为2=4頁+y,原来他消费9单位X,8单位y,现在乂减少到4单位，问需要消费多少单位），才能与以前的满足相同？解：HZ】=4蔚+8=2（）：卩=4丽+尹=8+”TU}=TU2^y=U.8•某消费者每月收入800元，用于购买x和Y两种商品，他(2)nCPyIx-Px+yPy=ryx6"15l6x+15v=7,x21230由于777]=TU2=>xj]=x2y2=>2003x40=—x12r30(1)为实现效用最大化，他应购买X和y各多少?(2)如果x的价格不变，Y的价格上涨50%,他的消费支出必须增加多少才能维持最初的效用水平?(3)如果(=6,Pv=15收入仍然为800元，为实现效用最大化，他应购买X和丫各多少?解:(1)Px=6.Py=10.1=800./(x?y)=TU=dfy=±ox=^_6"10=>叮匕》、x-Px+y-Pv=I6x+10y=800⑵Px=6，Py=\5Jgy)=TU=xy,假设现在收入为厂n/'=4(XX/&A/=/'—/=400舲一800.200809•假定某消费者的效用函数为：他会把收入的多少用于商品y上？200讨_4°3、x・Px+y・Py=ly_xx-Px+y-Py=20011.对于下面的柯布道格拉斯生产函数:e=ioL°5-/c（,s10•某消费者每月收入200元，全部用于购买X和丫两种商品，他的效用函数为：TU=xy,X和丫两种商品的价格分Pv,求该消费者对X和丫两种商品的需求函数。解：令fgy）=TU=xy妙0=叮P『Ix*Px+y*Pv=200如果L与K同时增加到原来的兄倍，那么它的产量将是原来产量的多少倍？解：令/（厶K）=0=1O・0°'・K°6n/（竝UK）=10（如严（宓尸・・=10-211・少・K"/（久LMK）__n/（厶K）一10・fK°6一•3512・已知某厂商生产某产品的生产函数为：2=又设Pl=3,Pk=5,试求：4Py兀（1）产量2=10时的最低成本支出和使用的厶与K的数量。(2)总成本为160,厂商实现均衡时的0、厶与K的数值。35解：令f(L^K)=Q=ljK^0更色•厶討)•竄.(1)尘二坐=>---------=---------aL=K乙件35—L=K=Q=W,TC=L・Pl+K•匕=3£+5K=80堂1吐*丄•(2)也=4=------------=--------=L=K巴竹35TC=L-Pl+K・Pf=3L+5K=SL=SK=160^>L=K=0=20・13.已知某企业生产某产品的生产函数为:Q=20厶+50K-6厂—2K?，Q的价格匕=15,K的价格Pk=3(),总成本TC=660.试求该企业的最优要素组合方式。解：令/（厶,K）=Q=20A+5（）K一6厶$-2K2df5f20—12厶_50-40K^L=dK_~15-_30Pk=>'L・Pi+K・Pk=660I15厶+30K=660=>厶=3,K=20.514.假设某产品生产的边际成本函数是：MC=3Q2_8Q+10（b若生产5单位产品时总成本是595,求总成本函数、平均成本函数、可变成本函数、平均可变成本函数。=>5’一4x5-+100x5+加=595=>ni=7015.某完全竞争厂商的短期成本函数为：STC（e）=0.0ie3-2Q2+1502+10,试求该厂商的短期供给函数。解：STC（Q）=0.0123-2Q2+1500+10MC=0.0302_40+150AVC：=0.020—2,令,4VC二0nQ二100nS.P=0.0322-4O+150((?>100)16.设某完全竞争厂商产品的价格为59元，STC(0)=4Q2+50Q+5,求厂商能获最大利润的产量及最大利润。解：tt(O)=TR(O)-STC(0)=590-...