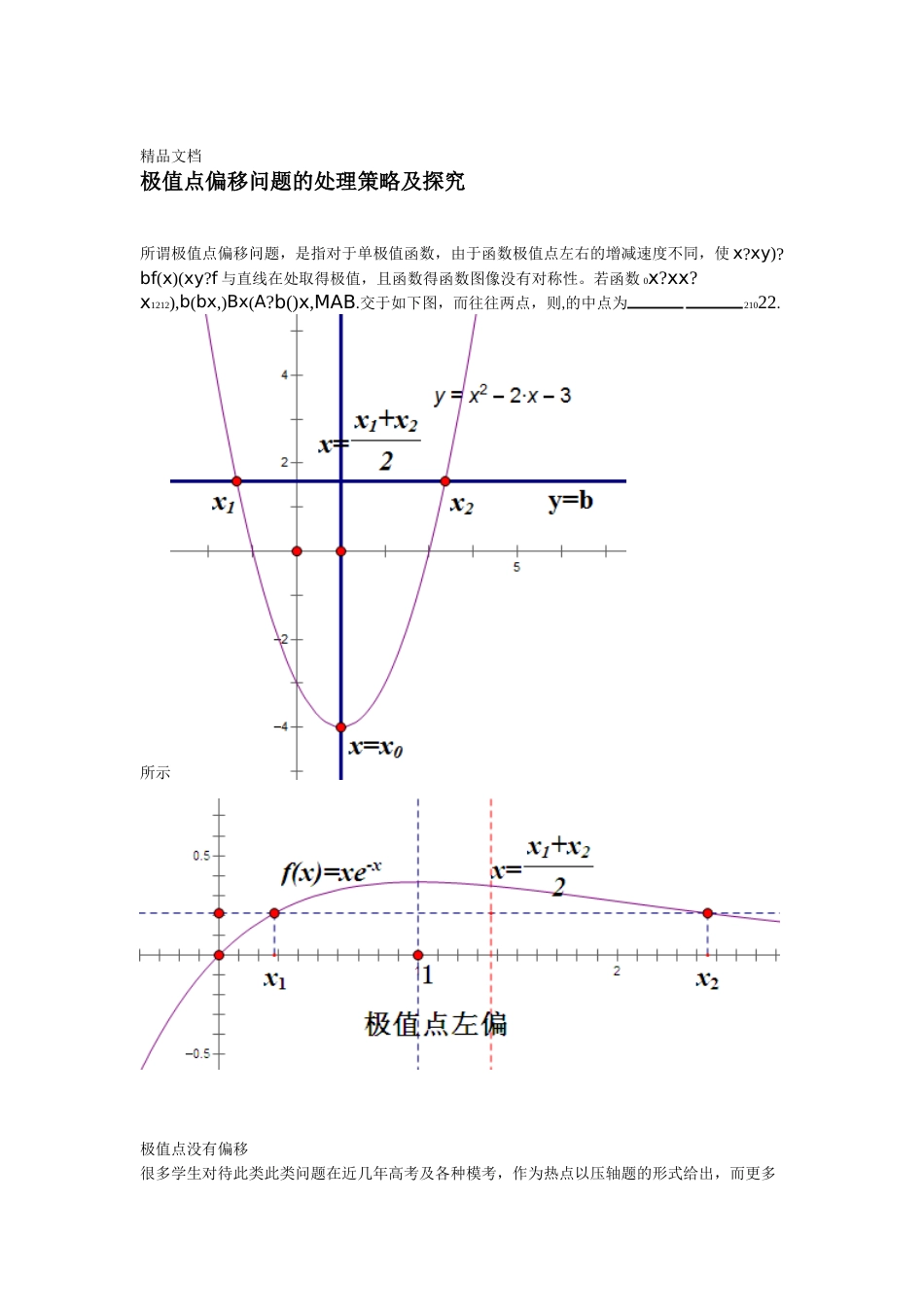
精品文档极值点偏移问题的处理策略及探究所谓极值点偏移问题，是指对于单极值函数，由于函数极值点左右的增减速度不同，使x?xy)?bf(x)(xy?f与直线在处取得极值，且函数得函数图像没有对称性。若函数0x?xx?x1212),b(bx,)Bx(A?b()x,MAB.交于如下图，而往往两点，则,的中点为21022.所示极值点没有偏移很多学生对待此类此类问题在近几年高考及各种模考，作为热点以压轴题的形式给出，而更多的题型又是有些题型是不含参数的，而且此类问题变化多样，问题经常是束手无策。参数如何来处理？是否有更方不含参数的如何解决？含参数的又该如何解决，含有参数的。我们先来看看此类问题的基方法也就有很多，便的方法来解决？其实，处理的手段有很多，本特征，再从几个典型问题来逐一探索！【问题特征】【处理策略】精品文档．精品文档一、不含参数的问题.?x)?R)?xe(xf(x)(x(x)?fx?xf，如果，例1.（2010天津理）已知函数，且21212.x?x?证明：21x??e)?xx)?(1f(,1)??)(f(x上，易得在【解析】法一：???x)(1,??，递增，在减，时上单调单调递???x0?x)f(x)???f(0)?0f(函时，，，，1?(f)1(1)f(x)f1x?.，且处取得极大值数在,如图所示ex1?0?x?),x?xx?x?f(x)f(x，则必有，不妨设，由21122211(0,1]x??x),(1?x)?f(1xF()?f，构造函数xx2???0?ex)??1)x)?f)(1?x?f((1F?((0,1]?x)xF(上单调递增，，所以在则1?xe(0,1]?x)xx)?f(1?F(x)?F(0)?0f(1?.恒成立对，也即(0,1]?1?x?x?1?x0由，，则112(f)?x))?f((2?x)?f(1?(1?(1)xxf(2?x)?f(x)f?(1?x))?f，即所以，2112111)???(1,?x,x2)??)(1,f(x又因为，且在上单调递减，212.x?xx?x?2?，即证所以2211)(1,??,x??x1?x2?x?x?x2x?2?x0?，，由法一知故法二：欲证，即证，22121121)x?f(x)f(x)xf()?f(2?)??(x)(1,f，在上单调递减，故只需证，又因为又因为2211)xf(2?f(x)?(0,1)?),x?f(2?xH(x)?f(x)，则等价于证明，构造函数故也即证11(0,1)x0?(x)?H.对恒成立x1?2x?2???0??e)x)?fx()?f)(2?x?(1H((0,1)?x)xH(所以上单调递增，由在则，xe2x?x?(0,1)?((1)?0Hx)?0x)H(x?H.恒成立，故原不等式，即已证明对亦成立21xx?xx?x?2?e)xf)f(x?(e?xex，化简得法三：由?，，得…21122121x1精品文档．精品文档x?xo?x?1?xt?x?xt?0,x?t?x，代入?，由法一知，式，不妨设.令，则11221212t?xt2tt1?ex?x?2t??t?x?x?x?2x，，则，反解出得，故要证：211211ttx1e?1e?12ttt?1)?0t?2)(e2t?(0?e1?2??t…?，等价于证明：即证：，，又因为te?1ttt???(t)?te?0(t?1)e?1,?(t?2)(e?1),(t?0)GG(t)?2G(t)?t，构造函数，则???(0)?0G(t))?Gt?(0,G??(t)t?(0,??)G)(t上单调递也在故从而在上单调递增，，x?x?20(0)?G(t)?G成立增，.，即证?式成立，也即原不等式21x2?lnx?lnx?x?lnxe，也即式，两边同时取以为底的对数，得法四：由法三中?1212x1x?12xxxx?xlnx?lnxx?lnlnx211221212)x(x??lnx?x??ln1?，从而，2121xxxx?xx?xx?x1?211121212x1xt?12(t?t?1)x?x?2lnt?2…令，等价于证明：，则欲证：?，21xt?112?1?2ttlnt(t?1)lnt2?(t)?M1)t?t)??(1?)lnt,(M(，则，构造21)t?(t1t?t?12???1)t,(t?t?1?2tln?(t)1)t?2(?1tln?)()t?2t?2(ln?tt?1?lnt由于，，又令则?????(1)??0??)(t)(t?0)(t)t???t?(1,)?(1,，所以在恒成立，故对上单调递增，，?(t)?0M(t)Mt?(1,??)上单调从而递增，由洛比，故塔法则在知：?t?t)1t?1)lnt((?1)ln(t?lim?lim(lnt)t?lim?)?2limM(M(t)?2即证，即证，?t?1(t?1)t1x?11x?1x??xx?x?2式成立，也即原不等式?成立.21【点评】以上四种方法均是为了实现将双变元的不等式转化为单变元不等式，方法一、二利用构造新的函数来达到消元的目的，方法三、四则是利用构造新的变元，将两个旧的变元都换成新变元来表示，从而达到消元的目的.二、含参数的问题.xx?x?2xx,ae??xf()x.，求证：有两个不同的零点2.例已知函数2121精品文档．精品文档x?a?xe)f(x的两个实根，从而这一问题的两个零点，等价于方程【解析】思路1：函数的四种方法全都可以用；与例1完全等价，例1a2：也可以利用参数解答如下：这个媒介去构造出新的函数.思路x,x)f(x有两个零点因为函数，21x?)x?ae1(11，所以?xae?(2)x2?2xx)21)?(()ea(e?x?x?由，得：2121xx2x?x?2)ea(e??...