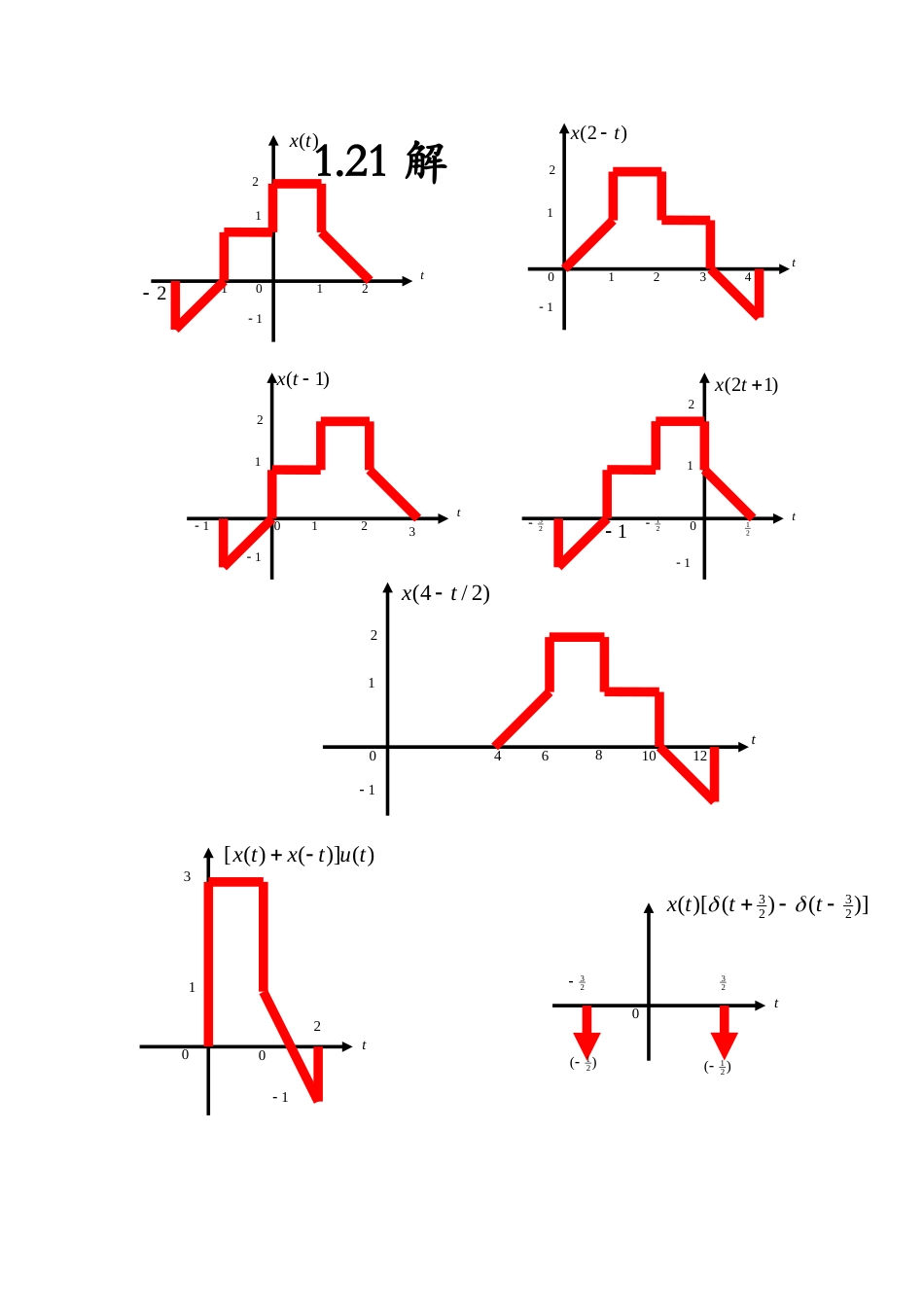
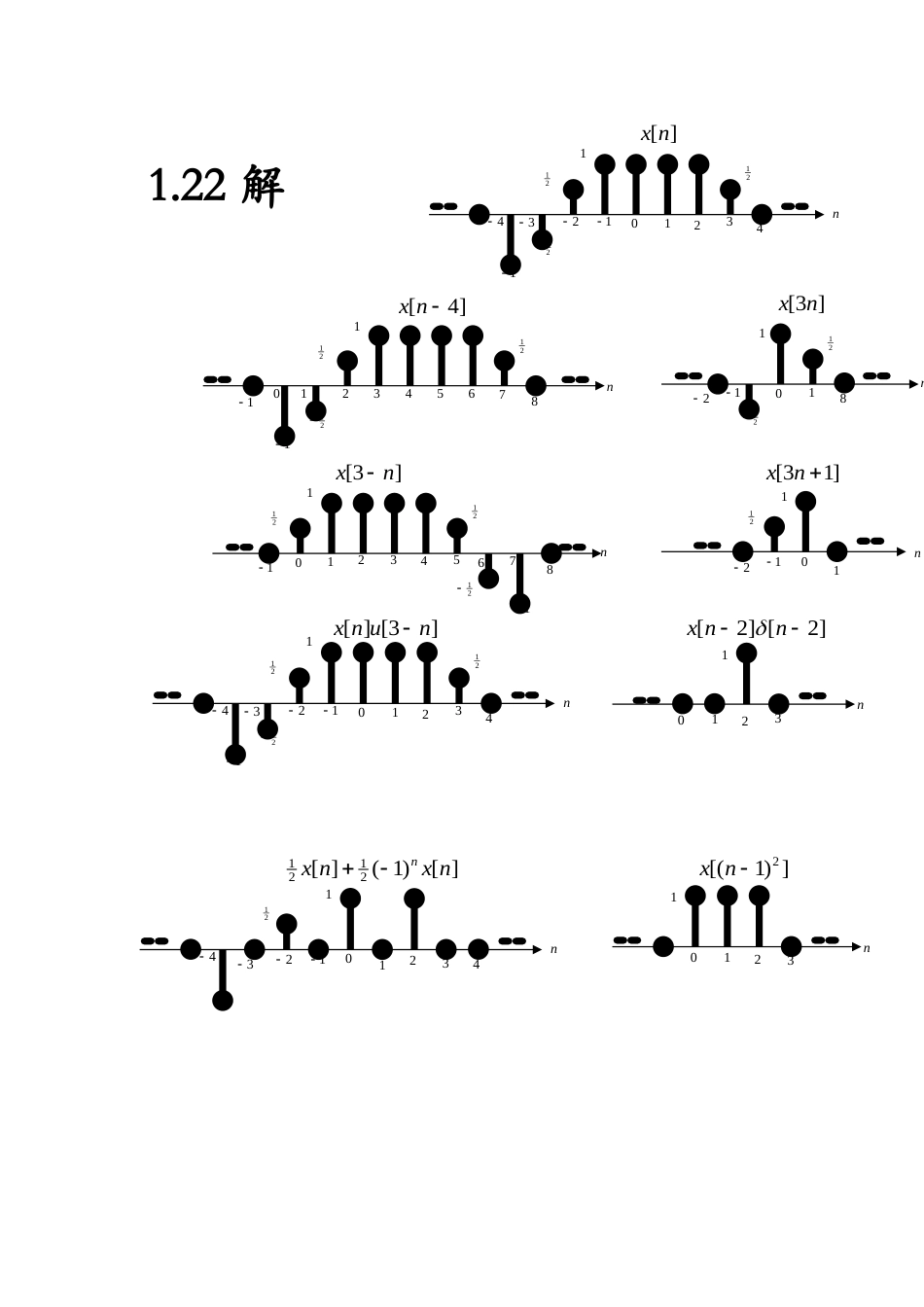
1.21解(t)x1012t1212()1tx1012t1213)(2tx012t12134)1(2tx231210t12121/2)(4tx08t121101246)]()([()tutxxt00t1312)]()()[(2323ttxt023t)(2123)(2110123432121211n[n]x4121.22解0123412121211n[4]nx567811012121211n][3nx23456781102121n3][nx1821011n]1[3nx212101231n2]2][[nxn012343211n[])1(][2121xnxnn4120123n)1][(2nx101234312121211n][][3nxnu4121.27解记忆时变可加齐次因果稳固A是是是是非是B非是是是是是C是是是是非非D是是是是是是E是否是非是是F是是是是非是G是否是是非非（a）)(22)(()txxtyt①由于(2)(2)(0)xxy，在t0的输出与前后时刻的输入都有关，所以系统是记忆的；②已知)(22)(()111txxtyt，)(22)(()222txxtty；当)(()012txttx时，)(2)2(()01012ttxtxtty，而)(22)()(010101ttxtxttyt，所以：)(()012tytty；因而系统是时变的；③已知)(22)(()111txxtyt，)(22)(()222txxtty，)(22)(()333txxtyt，当()()()213txxtxt时，)](2)(2[2)](2)([()21213txtxtxxtyt所以()()()213tyytyt，因而系统是可加的；当()()12axtxt时，())(22)(()1112ayttaxaxtty，因而系统是齐次的；综合系统的可加性与齐次性，所以系统是线性的；④由于(2)(2)(0)xxy，在t0的输出与t2的输入也有关，所以系统是非因果的；⑤如tBx)(，即输入有界，就：Btxxttxxtyt2)(22)()(22)(()，即输出有界；所以系统是稳固的；（b）[cos(3)].()()xttyt①可见，在t0t点的输出y(0t)仅与0tt点的输入有关非记忆；②已知()[cos(3)]()11xttyt，()[cos(3)]()22xttyt；当)(()012txtxt时，)([cos(3)]()012txttyt，而)(3)cos(3)(01001txttttyt，)(()012tytty，因而系统是时变的；③已知()][cos(3)()11xttyt，()[cos(3)]()22xttyt，()[cos(3)]()33xttyt，当()()()213xtxtxt时，()]()[cos(3)][()213xtxttyt，所以()()()213ytytyt，因而系统是可加的；当()()12axtxt时，()()][cos(3).()12ayttaxtyt，因而系统是齐次的；综合系统的可加性与齐次性，所以系统是线性的；④由于系统是非记忆的，所以系统是因果的；⑤如tBx)(，即输入有界，就：Bxttxttxtyt()cos(3).()cos(3).()()，即输出有界，所以系统是稳固的；（c）xdtyt2())(①t0t的输出y(0t)与)2,(0tt的输出有关，系统是记忆的；②当输入)(()01txtxt时，输出tdxtyt201)()(，令ts0，就s0t，那么)(()()()022100tytxxsdstytttt，因而系统是时变的；③已知xdtyt())(211，xdtyt())(222；令()()()213xtxtxt，就()()()]()[()212213ytytdxxtyt，因而系统是可加的；当()1()axtxt时，()()())(2211aytdaxdxtytt，因而系统是齐次的；综合系统的可加性与齐次性，所以系统是线性的；④xdy10()(5)，即t5时的输出y(5)与t(,10)间的输入都有关系统是非因果的；⑤如tBx)(，即输入有界，就：tttdBdxdxty222()()()，所以系统是不稳固的；（d）02),()(0,0()txttxtty①(2)(0)(0)xxy，即y(0)与2,0tt的输入有关，系统是记忆系统；②令)(()01txtxt，就02),()(0,002),()(0,0)(00111ttxtttxttxttxtyt而0000000002),()(,002),()(0,0)(tttxtttxtttttxtttxtttty)(()01tytyt，系统是时变的；③令()1()axtxt，就()02),()(0,01()ayttaxttaxtyt，所以，系统是齐次的；已知02),()(0,0)(111txtt...