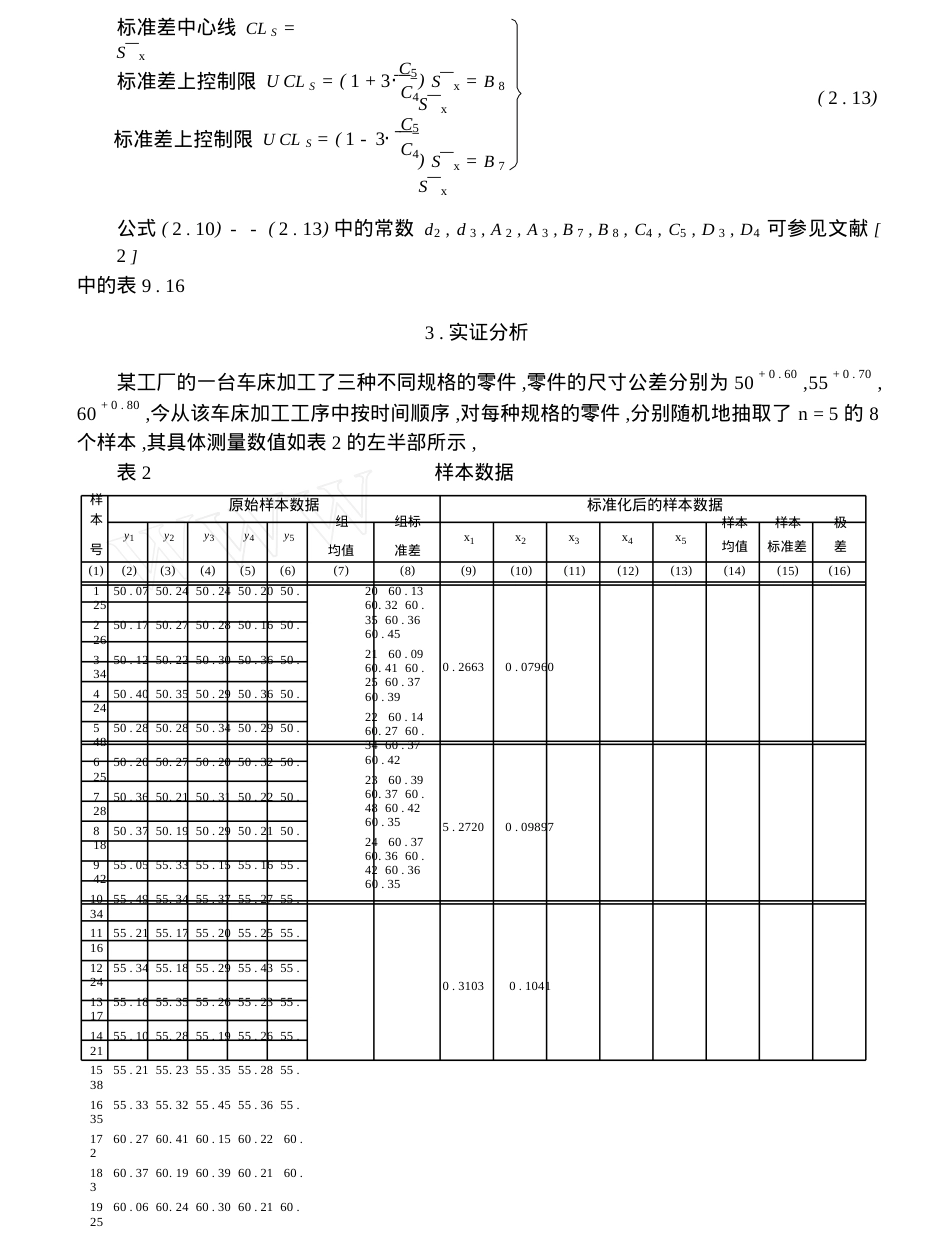
第一组第K组y(1)y(1)y(1)y(1)1my(1)y(1)y(K)11y(K)y(K)y(K)1my(K)y(K)多品种小批量生产情形下的工序质量控制图ΞΞΞ王建稳(北方工业大学经济管理学院,北京100041)摘要:在现代制造业中,企业经常出现多品种小批量的生产方式,且对不同品种的产品,其生产工序的质量特性值的分布一般是不同的,针对这种情况,本文建立了相应的¯X-R控制图和X¯-S控制图,并给出了实证分析关键词:多品种;小批量;控制图:O213.1文献标识码:A1.问题的提出现在的工序质量控制方法主要是针对单批量生产且质量特性值具有相同分布的情况而提出的,但随着市场经济的发展,为了更好地满足市场和顾客需要,企业在竞争激烈的条件下,往往采取的是多品种小批量的生产方式,追求品种、规格、型号的众多。对于不同品种的产品,其生产工序的质量特性值的分布一般都是不同的,例如,利用同一台设备,由同一位工人,在相同的环境条件下,多品种小批量地生产多种不同规格的零件,同一批零件的尺寸具有相同的分布,不同批零件的尺寸具有不同的分布,因此研究多品种小批量生产情形下的工序质量控制方法就具有十分重要的现实意义。当不同批的工序质量特性值的方差相同时,即在同等工序能力下,文献1提出了相应的工序质量控制方法,但大多数情况下,不同批的工序质量特性值具有不同的期望和方差,对此,本文主要建立了相应的¯X-R控制图和¯X-S控制图,并给出实证分析。2.多品种小批量生产情况下的¯X-R控制图和¯X-S控制图假设某道工序在一段时间内小批量地生产了表1样本数据结构K种不同规格的零件,今从该工序中按时间顺序利用即时法从第k批产品中抽取了nm11(k=1,2,,K)件零件,即每批产品选取m21个时间点,每个时间点连续抽取n件,得样本数据如表1:一般来说,在工序处于统计控制状态下2m212my(k)2ij～N(μkσ,k)k=1,2,,K,i=1,2,,n,j=1,2,,m这时,要使所得到的K组服从不同分布的质量特性值数据能够在同一个控制图中表示出kki(k(klΦiiR·来,则应对K组数据各自进行标准化,即令xk=yij-μkijAk则:xk～N(0,1)k=1,2,,K,i=1,2,,n,j=1,2,,m但μk,A2是未知参数,其估计量为μ^k=¯y(k)=1nm66y(k),(2.1)nmi=1j=1ijnmσ^2=S2=166(y(k)-¯y(k))2,(2.2)kknm-1i=1j=ij(k)(k)于是,标准化数据x(k)=yij-¯y,(2.3)则x(k)ijSkij独立同分布,且近似服从标准正态分布N(0,1),令n¯xj=16xij,j=1,2,,mk=1,2,,K(2.4)R(k)ni=1max(k)min(k)j=lΦiΦn{xij}2{xij},j=1,2,,mk=1,2,,K(2.5)j=1n6(xij-¯xj),j=1,2,,mk=1,2,,K(2.6)S(k)n-1i=1(k)(k)2"x=1mK66¯x(k)(2.7)mKj=1k=1jR¯x=1mK66R(k)(2.8)mKj=1k=1j¯Sx=1mK66S(k)(2.9)mKj=1k=1j易验证"x=0。此时,对于标准化后的数据x(k)来说,平均值和极差控制图(X¯-R图)控制界限的计算公式为:均值中心线CL¯x="x=0均值上控制限UCL¯x="x+3·1R¯x=A2R¯xnd2(2.10)均值下控制限LCL¯x="x-3·1R¯x=-A2R¯x极差中心线CLR=R¯xnd2d3极差上控制限UCLR=(1+3·d2极差上控制限UCL=(1-3d3d2)R¯x=D4R¯x)R¯x=D3R¯x(2.11)平均值和标准差控制图(X¯-S图)控制界限的计算公式为:均值中心线CL¯x="x=0均值上控制限UCL¯x="x+3·1¯xx=A3¯SxnC4(2.12)均值下控制限LCL¯x="x-3·1¯Sx=-A3¯SxnC4S·标准差中心线CLS=S¯xC5标准差上控制限UCLS=(1+3·C4标准差上控制限UCL=(1-3C5C4)S¯x=B8S¯x)S¯x=B7S¯x(2.13)公式(2.10)--(2.13)中的常数d2,d3,A2,A3,B7,B8,C4,C5,D3,D4可参见文献[2]中的表9.163.实证分析某工厂的一台车床加工了三种不同规格的零件,零件的尺寸公差分别为50+0.60,55+0.70,60+0.80,今从该车床加工工序中按时间顺序,对每种规格的零件,分别随机地抽取了n=5的8个样本,其具体测量数值如表2的左半部所示,表2样本数据样原始样本数据标准化后的样本数据本组组标号y1y2y3y4y5均值准差x1x2x3x4x5样本样本极均值标准差差(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)150.0750.2450.2450.2050.25250.1750.2750.2850.1650.26350.1250.2250.3050.3650.34450.4050.3550.2950.3650.24550.2850.2850.3450.2950.48650.2050.2750.2050.3250.25750.3650.2150.3150.2250.28850.3750.1950.2950.2150.18955.0555.3355.1555.1655.421055.4955.3455.3755.2755...