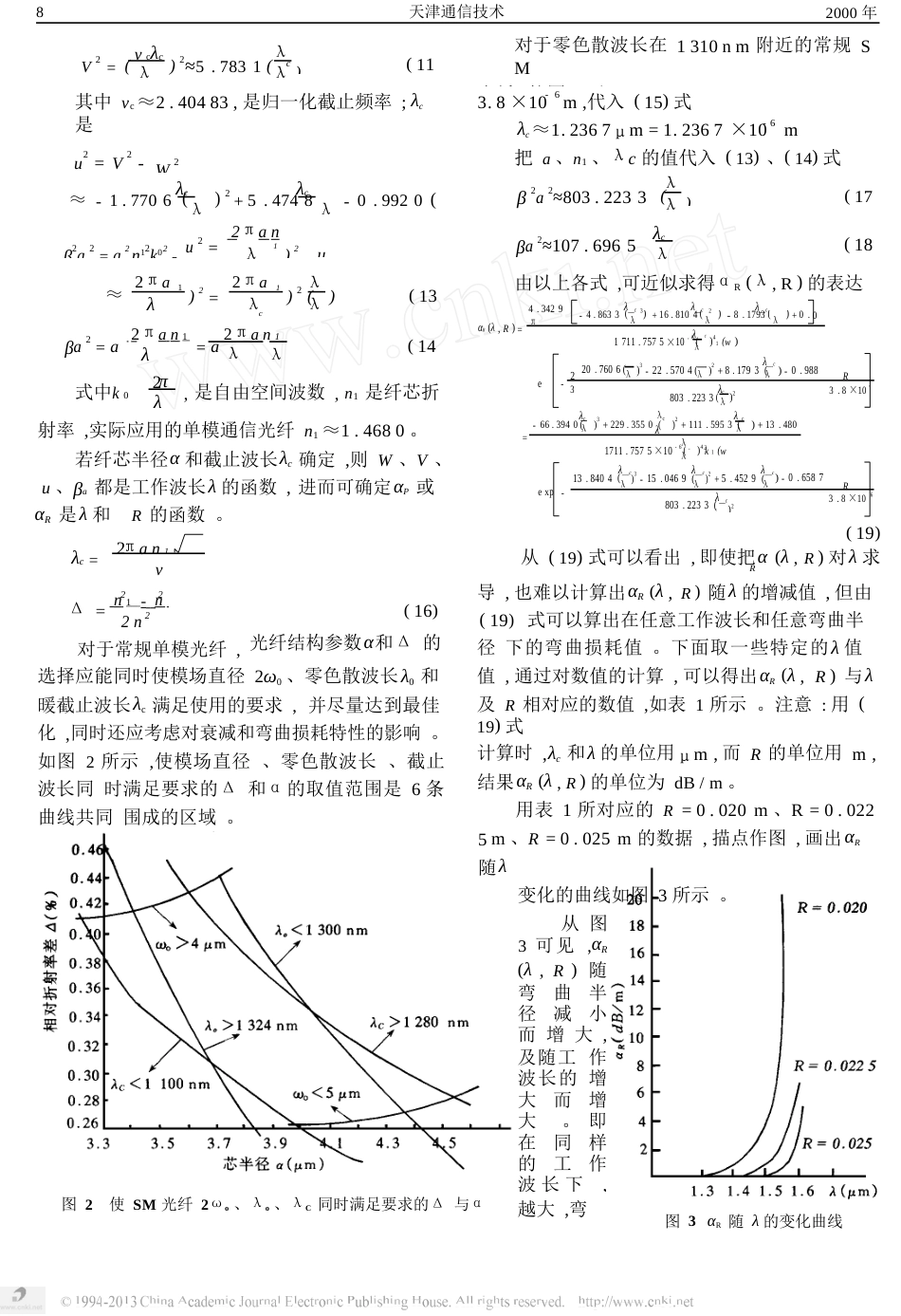
单模光纤弯曲损耗与波长及弯曲半径的关系刘世春黄治逊(天津电信网管维护中心,天津300012)摘要:对在弱导条件下的单模光纤弯曲损耗进行了定量分析,导出了弯曲损耗的函数αR(λ,R)。关键词:波长;弯曲半径;弯曲损耗中图分类号:TN929.1文献标识码:A文章编号:1006-7442(2000)02-0007-03设单位弧长上的弯曲损耗dB数为αR,(1)式可得:光纤在实际应用中,不可避免地要发生弯曲,而产生光纤弯曲损耗。光纤弯曲可模仿成如图1所示的弯曲波导。则由Piexp(-αP)αR=-10Lg=4.3429αPPi4.3429πwu232wR)(2)=exp(-223aaβ2βa2(1+w)v2k2(w1式中u是径向归一化相位常数;W是径向归一化衰减常数;V是归一化频率;α是纤芯半径;R是弯曲半径;K1(w)是一阶第二类修正的贝塞尔函数,如式(3):Υ+Ln(w)k1(w)=I1(w)+I0(w)/w-A(3)2图1弯曲波导示意图据光纤理论,在正常情况下,光在光纤里沿轴向传播的常数β应满足关系式:n2k0<β<n1k0。当光纤弯曲时,光电磁波在弯曲部分中进行传输,要想保持同相位的电场和同相位的磁场在一个平面里,即保持导行的情况,那么越靠近外侧,其速度就会越大(即β越小)。待到一定的地点时,其相速就会等于所在物质中的光速,待超过这一地点式中:Υ≈0.577216,是欧勒常数;(W)2n+∞2I1(w)=∑(4)n=0n!(n+1)!(w)2∞2I0(w)=∑(5)n=0(n!)2∞n(w)2n-2(1+1+1)∑(6)后,电磁波就会成为辐射波,即β<nk,导波成为A=+220(n!)2nn=1辐射波。如把从这一点起到无穷远处的能量进行积分,就是在光纤弯曲部分中传输所损耗的能量或损耗功率。对光纤弯曲损耗的理论分析是很复杂的,有几种近似公式,但它们相互之间的差别很大。下面即参照LucB·Jeunhomme理论进行分析。首先把弯曲光纤场的分布近似成薄膜介质带由(2)式可以看出弯曲损耗αR随弯曲半径R的减小而增大,但看不出αR随波长λ增减的变化趋势。对于单模光纤在弱导条件下有:W≈2.7484λc-0.9960(7)λλcλc1+W=2.7484λ-0.9960≈2.7484λ(8)λcλcW2=7.5537(λ)2-5.4748λ+0.9920(9)λcλcW3=20.7606(λ)3-22.5704(λ)2+上的功率衰减系数αP,如式()1:λc8.1793λ-0.9880wu2π2w3RαP=2β(10)exp(-)(1)3β2aa2(1+w)v2k1(w)天津通信技术2000年8对于零色散波长在1310nm附近的常规SM光纤,按图2,取Δ=0.36%=0.0036,a=3.V2=(vcλc)2≈5.7831(λc)(11)λλ其中vc≈2.40483,是归一化截止频率;λc是截止波长。3.8×10-6m,代入(15)式得:λc≈1.2367μm=1.2367×10m。-6把a、n1、λc的值代入(13)、(14)式,则有:u2=V2-W2λcλcλc2a2≈803.2233)β((17)≈-1.7706(λ)2+5.4748λ-0.9920(12)λ2πanλc1)2βa2≈107.6965β2a2=a2n2k2-u2=u(18)λλ102πan2πan由以上各式,可近似求得αR(λ,R)的表达式:λc1)2=1)2()≈((13)λλλ32cαR(λ,R)=βa2=a2πan1=a2πan1λ1711.7575×10-6(c)4k2(14)λ1(w)λλcλ20.7606()3-22.5704()2+8.1793()-0.9880π2exp-式中k0=,是自由空间波数,n1是纤芯折λc3.8×10-6λλλcλλ-66.3940()3+229.3550()2+111.5953()+13.4800cc射率,实际应用的单模通信光纤n1≈1.4680。若纤芯半径α和截止波长λc确定,则W、V、u、βa都是工作波长λ的函数,进而可确定αP或λλλ=λc1711.7575×10-6()4k1(w)2λ13.8404()3-15.0469()2+5.4529()-0.6587exp-6)803.2233(2αR是λ和R的函数。(19)从(19)式可以看出,即使把α(λ,R)对λ求πan12λc=vcR导,也难以计算出αR(λ,R)随λ的增减值,但由(19)式可以算出在任意工作波长和任意弯曲半径下的弯曲损耗值。下面取一些特定的λ值22Δ=n1-n2(16)光纤结构参数α和Δ的22n1对于常规单模光纤,值,通过对数值的计算,可以得出αR(λ,R)与λ选择应能同时使模场直径2ω0、零色散波长λ0和暖截止波长λc满足使用的要求,并尽量达到最佳及R相对应的数值,如表1所示。注意:用(19)式计算时,λc和λ的单位用μm,而R的单位用m,结果αR(λ,R)的单位为dB/m。用表1所对应的R=0.020m、R=0.0225m、R=0.025m的数据,描点作图,画出αR随λ变化的曲线如图3所示。从图3可见,αR(λ,R)随弯曲半径减小而增大,及随工作波长的增大而增大。即在同样的工作波长下,化,同时还应考虑对衰减和弯曲损耗特性的影响。如图2所示,使模场直径、零色散波长、截止波长同时满...