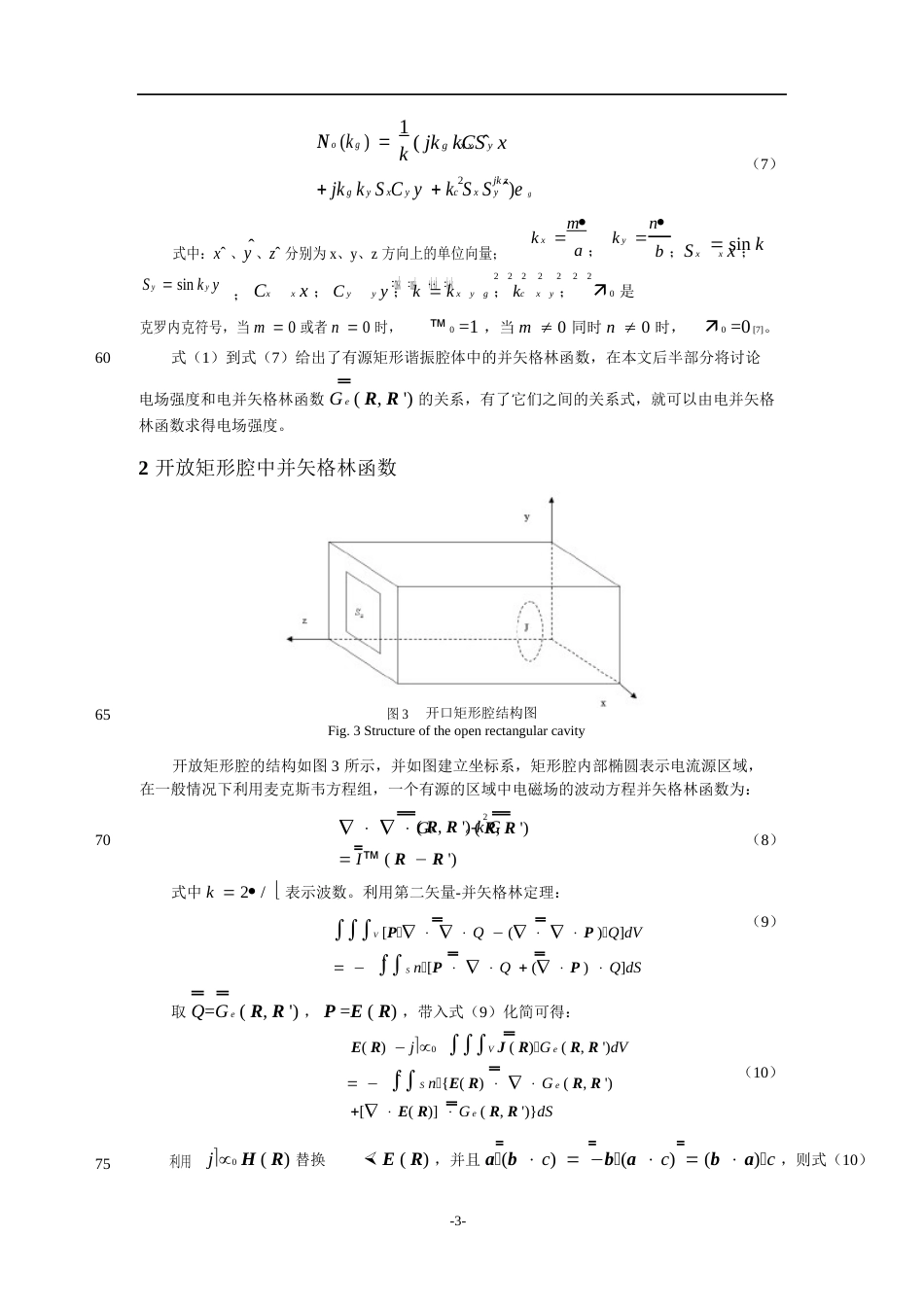
开口矩形腔体中场分布的研究#陈立伟，关茵*（哈尔滨工程大学信息与通信工程学院，哈尔滨150000）5101520253035摘要：本文使用并矢格林函数对开放式矩形腔体中的电磁场分布进行了讨论，并且针对抛物面天线进行了分析，最终得出了开口矩形腔体中的场分布公式。使用并矢格林函数对开放式腔体内的场分布和抛物面天线进行分析是本文的创新之处。最终应用本文得出的并矢格林函数方法使用MATLAB进行了数值计算，得出了开口矩形腔中的电场强度分布值，同时还使用FEKO对开口矩形腔中的电场分布进行了软件仿真，最终的计算结果的对比证明了本文讨论的计算方法的正确性。关键词：并矢格林函数；MATLAB；FEKO中图分类号：O441.5InformationandCommunicationEngineeringCollege，HarbinEngineeringUniversity,Harbin,ChinaChenLiwei,GuanYin(InformationandCommunicationEngineeringCollege，HarbinEngineeringUniversity,Harbin150000)Abstract:Inthispaper,theopenrectangularcavityfielddistributionandparabolicantennaareanalyzedbyusingtheDyadicGreen’sfunctions.Finallythefielddistributionofopenrectangularcavityisconcluded.TheinnovationofthisarticleisusingtheDyadicGreen’sfunctionstoanalyzedopencavityfieldandparabolicantenna.TheelectricfieldiscalculatedbyMATLAB,andtheresultsaregottenbysimulationofFEKO.Thefinalresultprovesthatthemethodisavailable.Keywords:DyadicGreen’sfunctions;MATLAB;FEKO0引言由于近些年来混响室在电磁兼容方面的应用[1]，对于矩形腔体内的场分布研究大多使用并矢格林函数方法[1,2]，但是对于开放式矩形腔体的场分布的相关研究还很少，而且在混响室研究中，一般都使用线天线作为信号源，这样就可以将信号源化简为电流源来研究[3]，而对于矩形腔体内的抛物面天线研究很少有人涉及，本文在有关开放式矩形腔体和矩形腔体中的抛物面天线方面都做了较深入的研究，并用试验结果证明了本文所述方法的正确性。1矩形腔体中的并矢格林函数本文的研究对象是有一个前端开口的矩形腔体构成的，其结构如图1所示。图1开口矩形腔体的结构图Fig.1Structureoftheopenrectangularcavity基金项目：国家自然科学基金(61102105,61102106,60775060);中国博士后科学基金（No.20080440840）；教育部博士点基金（No.20102304120014,20102304110006）；黑龙江省自然科学基金(F201029,）作者简介：陈立伟，（1974-），女，副教授，语音处理。E-mail:286110024@qq.com-1-ˆˆ∑,mn2⎪abkksinkl[Meo(l−z)M'eo(z)⎪−⎪Noe(l−z)N'oe(z')](zz')⎪2∑(2−0)[Meoeo(l−z')⎪abm,nkcggl(z)M'ksink−⎪⎩Noeoe(l−z)](zz)(z)N'l(z)[M(−k)−M(k(z)[N(−k)N(kˆxy图1所示腔体中的圆形表示受试的抛物面天线，前端为开口，尺寸如图所示，从图1可以看出，开口矩形腔体就是一个前端开口的矩形谐振腔。40图2矩形腔结构图Fig.2Structureoftherectangularcavity图2为一个全封闭的矩形谐振腔，椭圆区域表示腔体中的电流源，如图2建立坐标系，45矩形腔体的长宽高分别为l、a、b。将波动方程表示为它的并矢格林函数形式[4,5]，即∇∇Ge(R,R')-k2Ge(R,R')I(R−R')和完纯导体矩形腔的边界条件nGe(R,R')0（在边界处，即x0,xa和y0,yb和z0,zl）就可求得矩形腔中的并矢格林函数的表达式[6,7]：Ge(R,R')−1k2zz(R−R')⎧2(2−0)'cgg⎨2⎪''（1）50式中：Meo(l−z)sin（kg）Me(kg)−ejkglMeo(z)（2）Noe(l−z)−jsin(kgl)No(kg)ejkglNoe(z)（3）jMeoegeg)]21Noeogog)]2Me(kg)(−kyCxSyx（4）（5）55kxSCyˆ)ejkgz（6）-2-xxˆjkgkySxCyykcSxSyˆ)egkx式中：xˆ、y、zˆ分别为x、y、z方向上的单位向量；kyb；Sxxx；Cxxx；Cyyy；kkxyg；kcxy；0是coskcoskkkkk∇∇Gee(R,R')(R,R')-kGˆˆNo(kg)1k(jkgkCSyx（7）2jkzˆma；nsinkSysinkyy；2222222...