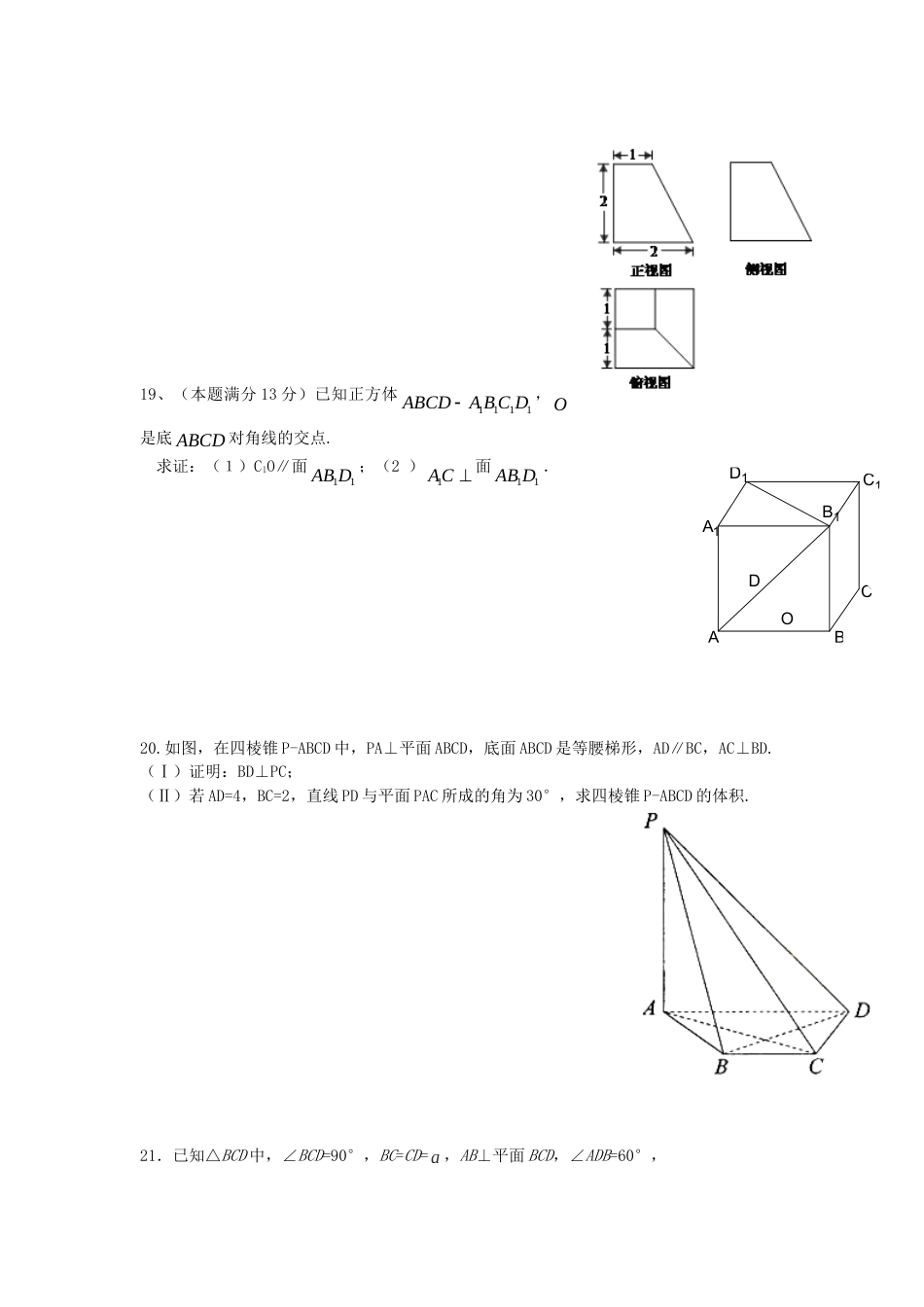
重庆清华中学高2015级高二年级第一次月考数学试题(理科)2013.10一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.经过空间任意三点可作平面(D)A.有且只有一个B.两个C.无数多个D.只有一个或有无数多个2.一个几何体的三视图如图所示,则该几何体可以是(C)A.棱柱B.棱台C.圆台D.圆柱3.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是(C)A.圆锥B.球体C.圆柱D.以上都有可能4.分别在两个相交平面内的两条直线间的位置关系是(D)A.异面B.平行C.相交D.以上都有可能5.如图,空间四边形ABCD中,EFGH,,,分别为BAADDCCB,,,边上的中点.则下列说法中不正确的是(C)A.四边形EFGH为平行四边形B.直线AC//平面EFGHC.若棱ACBD,则四边形EFGH为矩形D.若棱ACBD,则四边形EFGH为菱形6.设m,n是两条不同的直线,,是两个不同的平面,则(B)A.若,////nm,则m//nB.若m//n,m,则nC.若//,//mm,则//D.若,m//,则m7.如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是(A)A.8cmB.6cmC.2(1+)cmD.2(1+)cm8.一个长方体的相邻三个面的面积分别为2,3,6,且这个长方体的各顶点都在同一个球面上,则这个球的表面积是(C)A.27B.56C.14D.16BCADEFGH9.如图,正方体1111ABCDABCD的棱长为1,线段B1D1上有两个动点E,F,且22EF,则下列结论中错误的是(D)A.ACBEB.三棱锥ABEF的体积为定值C.EF∥平面ABCDD.△AEF与△BEF的面积相等10.如图:直三棱柱ABC—A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B—APQC的体积为(B)A、2VB、3VC、4VD、5V二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卡相应题号的横线上)11.三个平面可以把空间最多分为_________个部分。12.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为________13.已知圆台上下两个底面半径分别为1和2,侧面积为5,则其母线长为_________.14.如右图是一个几何体的三视图,其体积为33,则a=______________15.如图,正方体1111ABCDABCD的棱长为1,P为BC的中点,Q为线段1CC上的动点,过点,,APQ的平面截该正方体所得的截面记为S,则下列命题正确的是___(写出所有正确命题的编号).①当102CQ时,S为四边形;②当12CQ时,S为等腰梯形;BPA1QC1B1CAa3211③当34CQ时,S与11CD的交点R满足113CR;④当314CQ时,S为六边形;⑤当1CQ时,S的面积为62.【答案】①②③⑤三、解答题(本大题共6小题,共75分,解答只写出文字说明、证明过程或演算步骤)16.(本题满分13分)如图所示,在正方体1111ABCDABCD中,,,,EFGH分别为棱111,,,CCBCABDC的中点.(1)求证:点,,,EFGH四点共面;(2)求证:平面A1BC1//平面EFGH.17.(本题满分13分)如图,在三棱锥P-ABC中,PA底面ABC,D是PC的中点,已知2BAC,AB=2,AC=23,PA=2.(1)求三棱锥P-ABC的体积(2)求异面直线BC与AD所成角的余弦值。18.已知某四棱台的三视图如图所示,根据所标数据求出该四棱台的表面积和体积。PBACDFHGECABD19、(本题满分13分)已知正方体1111ABCDABCD,O是底ABCD对角线的交点.求证:(1)C1O∥面11ABD;(2)1AC面11ABD.20.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.(Ⅰ)证明:BD⊥PC;(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.21.已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,D1ODBAC1B1A1CE、F分别是AC、AD上的动点,且(01.)AEAFACAD(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;(Ⅱ)求二面角A-CD-B的正切值;(Ⅲ)当λ为何值时,平面BEF⊥平面ACD?20.【解析】(Ⅰ)因为,,.PAABCDBDABCDPABD平面平面所以又,,ACBDPAAC是平面PAC内的两条相较直线,所以BD平面PAC,而PC平面PAC,所以BDPC.(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD平面PAC,所以DPO是直线PD和平面PAC所成的角,从而D...