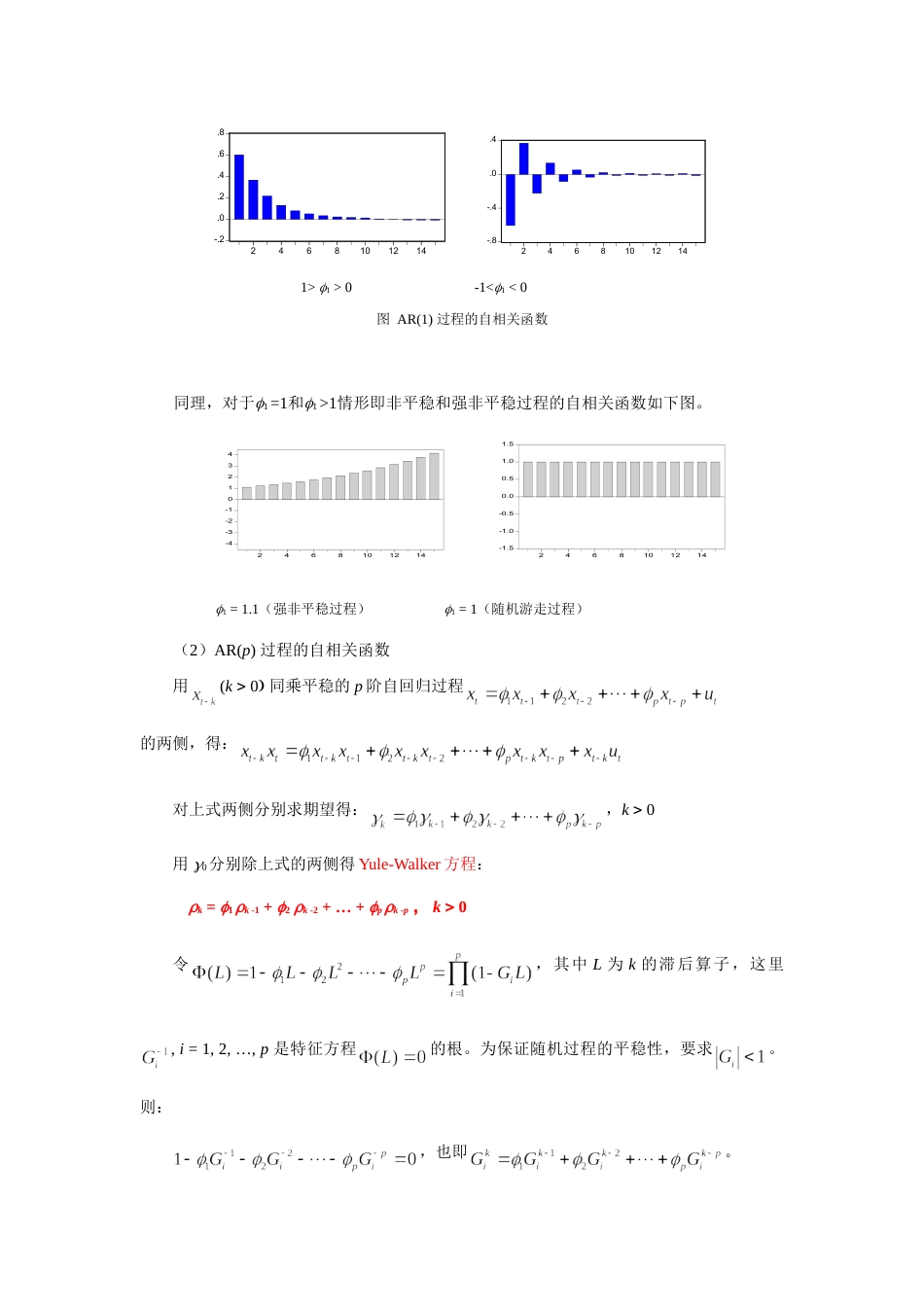
自相关函数与偏自相关函数上一节介绍了随机过程的几种模型。实际中单凭对时间序列的观察很难确定其属于哪一种模型，而自相关函数和偏自相关函数是分析随机过程和识别模型的有力工具。1、自相关函数定义在给出自相关函数定义之前先介绍自协方差函数概念。由第一节知随机过程{}中的每一个元素，t=1,2,…都是随机变量。对于平稳的随机过程，其期望为常数，用表示，即，随机过程的取值将以为中心上下变动。平稳随机过程的方差也是一个常量，用来度量随机过程取值对其均值的离散程度。相隔k期的两个随机变量与的协方差即滞后k期的自协方差，定义为：自协方差序列：，称为随机过程{}的自协方差函数。当k=0时，。自相关系数定义：因为对于一个平稳过程有：所以，当k=0时，有。以滞后期k为变量的自相关系数列（）称为自相关函数。因为，即=，自相关函数是零对称的，所以实际研究中只给出自相关函数的正半部分即可。2、自回归过程的自相关函数（1）平稳AR(1)过程的自相关函数AR(1)过程：，1。已知（why?）。用同乘上式两侧上式两侧同取期望：其中（why?）（由于xt=ut+1ut-1+12ut-2+…，所以xt-k=ut-k+1ut-k-1+12ut-k-2+…，而ut是白噪音与其t-k期及以前各项都不相关）。两侧同除0得：因为o=1，所以有（）对于平稳序列有。所以当1为正时，自相关函数按指数衰减至零；当1为负时，自相关函数正负交错地指数衰减至零。见下图。因为对于经济时间序列，1一般为正，所以第一种情形常见。指数衰减至零的表现形式说明随着时间间隔的加长，变量之间的关系变得越来越弱。-.2.0.2.4.6.82468101214-.8-.4.0.424681012141>>0-1<<0图AR(1)过程的自相关函数同理，对于=和>情形即非平稳和强非平稳过程的自相关函数如下图。-4-3-2-1012342468101214-1.5-1.0-0.50.00.51.01.52468101214=1.1（强非平稳过程）=1（随机游走过程）（2）AR(p)过程的自相关函数用(k同乘平稳的p阶自回归过程的两侧，得：对上式两侧分别求期望得：，k0用0分别除上式的两侧得Yule-Walker方程：k=1k-1+2k-2+…+pk-p，k0令，其中L为k的滞后算子，这里,i=1,2,…,p是特征方程的根。为保证随机过程的平稳性，要求。则：，也即。可证：（*）其中Ai,i=1,…，p为待定常数。（提示：可把（*）式代入到Yule-Walker方程中证明）由（*）式知道会遇到如下几种情形。①当为实数时，（*）式中的将随着k的增加而几何衰减至零，称为指数衰减。②当和表示一对共轭复数时，设，，=R，则,的极座标形式是：若AR(p)过程平稳，则，所以必有R<1。那么随着k的增加，自相关函数（*）式中的相应项,将按正弦振荡形式衰减。注意：实际中的平稳自回归过程的自相关函数常是由指数衰减和正弦衰减两部分混合而成③从（*）式可以看出，当特征方程的根取值远离单位圆时，k不必很大，自相关函数就会衰减至零。④有一个实数根接近1时，自相关函数将衰减的很慢，近似于线性衰减。当有两个以上的根取值接近1时，自相关函数同样会衰减的很慢。-.4.0.42468101214-.4-.2.0.2.4.62468101214两个特征根为实根两个特征根为共轭复根图AR(2)过程的自相关函数3、移动平均过程的自相关函数（1）MA(1)过程的自相关函数。对于MA(1)过程，有：当k=0时，当k=1时，当k1时，综合以上三种情形，MA(1)过程自相关函数为k==-.4-.2.0.2.42468101214-.4-.2.0.2.424681012141010图MA(1)过程的自相关函数可见MA(1)过程的自相关函数具有截尾特征。当k1时，k=0。（2）MA(q)过程的自相关函数MA(q)过程的自相关函数是k=当kq时，k=0，说明k,k=0,1,…具有截尾特征。例如，对于MA(2)过程，自相关函数是1=,2=,k=0,k>2。4、ARMA(1,1)过程的自相关函数ARMA(1,1)过程的自相关函数k从1开始指数衰减。1的大小取决于1和1,1的符号取决于(1-1)。若1>0，指数衰减是平滑的，或正或负。若1<0，相关函数为正负交替式指数衰减。对于ARMA(p,q)过程，p,q2时，自相关函数的表现形式比较复杂，可能是指数衰减、正弦衰减或二者的混合衰减。5、相关图（correlogram，或估计的...