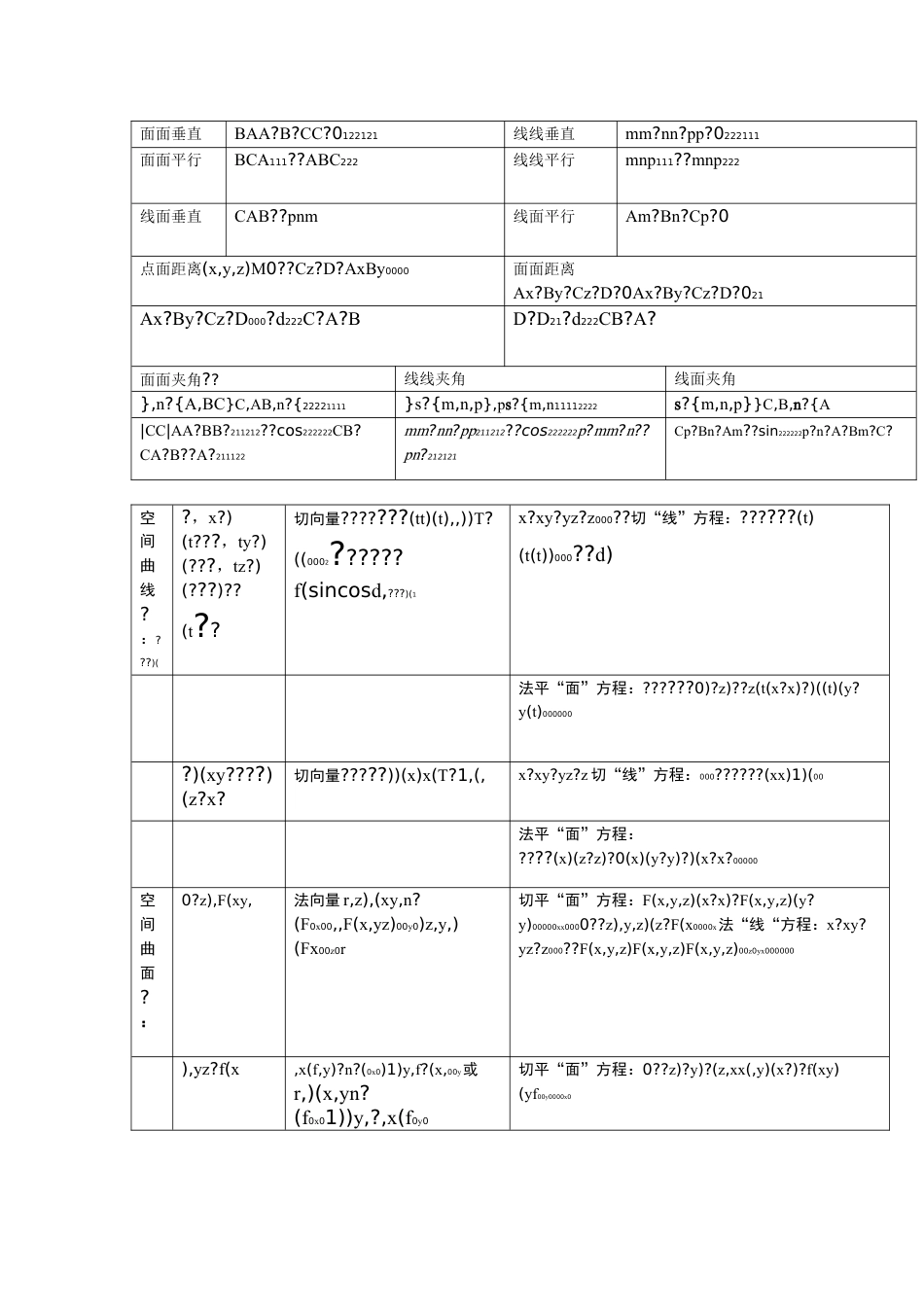
学习资料第八、九章向量代数与空间解析几何总结向量代数定义与运算的几何表达定义在直角坐标系下的表示?ai?aj?ak?(a,a,a)aruuuzxzyyxrrr向量aAB.记作或有大小、有方向a?prja,a?prja,a?prjazxyyxz222aaaaa?a??向量的模记作模zyx??ba?c?b?,a,a?b?ba?和差zxyzyxb－?aa?bcc?(a,a,a)azyx?e?e0a?，则单位向量aaa222aa?a?zxyaaay???xz?coscoscos??，，rrraaa???azx,y,，，，与设轴的夹角分别为方向余弦???cos，cos，cos则方向余弦分别为???)，，coscose?(cosa222????cos1?+coscos??cosbb?aa?为向量a与b的夹，bb?a?b?ab?aa点乘（数量积）zxyxzy角ijk?sinabc?叉乘（向量积）a?aaa?b?为向量a与b的夹角zxyb?a?cbbbacb与都垂直向量，zyx定理与公式a?b?ab?ab?ab?00?a?b?a?b垂直zxyzxyaaayzx???a//b0?a?b?a//b平行bbbzxyab?ab?abba?zxyxyz??cos??cos两向量夹角余弦交角余弦ba222222bb?b?a?a?a?zxxzyyab上的投影向量在非零向量bab?aab?zyxyxz?prjaa?b投影b??ab)prja?acos(222b??bbbbzxy平面直线M(x,y,zxM(,y,z))}pm{,n,T,{n?A,BC}?点方向向量法向量点00000000方程名称方程形式及特征方程形式及特征方程名称Ax?By?Cz?D?0?1111Ax?By?Cz?D?0一般式一般式?0?C政法???AxBy?2222x?xy?yz?z000??0?)?(?)?(AxxByyC)?(zz?点向式点法式000mnp仅供学习与参考．学习资料三点式x?xy?yz?z1110y?yx?xz?z?111222x?xz?yz?y133311参数式x?x?mt?0?y?y?nt?0?z?z?pt?0截距式zyx1???cba两点式x?xy?yz?z000??x?xy?yz?z000111面面垂直BAA?B?CC?0122121线线垂直mm?nn?pp?0222111面面平行BCA111??ABC222线线平行mnp111??mnp222线面垂直CAB??pnm线面平行Am?Bn?Cp?0点面距离(x,y,z)M0??Cz?D?AxBy0000面面距离Ax?By?Cz?D?0Ax?By?Cz?D?021Ax?By?Cz?D000?d222C?A?BD?D21?d222CB?A?面面夹角??线线夹角线面夹角},n?{A,BC}C,AB,n?{22221111}s?{m,n,p},ps?{m,n11112222s?{m,n,p}}C,B,n?{A|CC|AA?BB?211212??cos222222CB?CA?B??A?211122mm?nn?pp211212??cos222222p?mm?n??pn?212121Cp?Bn?Am??sin222222p?n?A?Bm?C?空间曲线?：???)(?，x?)(t???，ty?)(???，tz?)(???)??(t??切向量???????(tt)(t),,))T?((0002??????f(sincosd,???)(1x?xy?yz?z000??切“线”方程：??????(t)(t(t))000??d)法平“面”方程：??????0)?z)??z(t(x?x)?)((t)(y?y(t)000000?)(xy????)(z?x?切向量?????))(x)x(T?1,(,x?xy?yz?z切“线”方程：000??????(xx)1)(00法平“面”方程：????(x)(z?z)?0(x)(y?y)?)(x?x?00000空间曲面?：0?z),F(xy,法向量r,z),(xy,n?(F0x00,,F(x,yz)00y0)z,y,)(Fx00z0r切平“面”方程：F(x,y,z)(x?x)?F(x,y,z)(y?y)00000xx0000??z),y,z)(z?F(x0000x法“线“方程：x?xy?yz?z000??F(x,y,z)F(x,y,z)F(x,y,z)00z0yx000000),yz?f(x,x(f,y)?n?(0x0)1)y,f?(x,00y或r,)(x,yn?(f0x01))y,?,x(f0y0切平“面”方程：0??z)?y)?(z,xx(,y)(x?)?f(xy)(yf00y0000x0法“线“方程：x?xy?yz?z000??f(x,y)f(x,y)?100x0y0仅供学习与参考．学习资料总结第十章重积分计算方法积分类型典型例题利用直角坐标系（1）?(xb)2????f(x,f(x,y)dxdy?ydx)dyX—型?)(axP141—例1、例31D?(yd)2????f(x,y)dxdy?,ydy)dxf(xY—型?)(cy1D二重积分利用极坐标系）（2?????dI?,fyx使用原则D)；(含圆弧,直线段(1)积分区域的边界曲线易于用极坐标方程表示?22?)(x?y)为实数,被积函数用极坐标变量表示较简单(含(2)平面薄片的质量质量=面密度?P147—例5面积?????????df()cossin,dD???????2???0???20利用积分区域的对称性与被积函数的奇偶性）（3当D关于y轴对称时，（关于x轴对称时，有类似结论）?0f(x,y)对于x是奇函数，??即f(?x,y)??f(x,y)P141—例2??应用该性质更方便??是偶函数，dxdy2I?xf(,y),y)对于x(fx??D1?)yx,)即f(?x,y?f(??的右半部分是DD?1计算步骤及注意事项1．画出积分区域2．选择坐标系标准：域边界应尽量多为坐标轴，被积函数关于坐标变量易分离原则：积分区域分块少，累次积分好算为妙．确定积分次序3先积一条线，后扫积分域方法：图示法．确定积分限4注意：充分利用对称性，奇偶性5．计算要简便仅供学习与参考．学习资料三重积分I????dvy,z)f(x,?空间立体物的质量?度质量=密面积投...