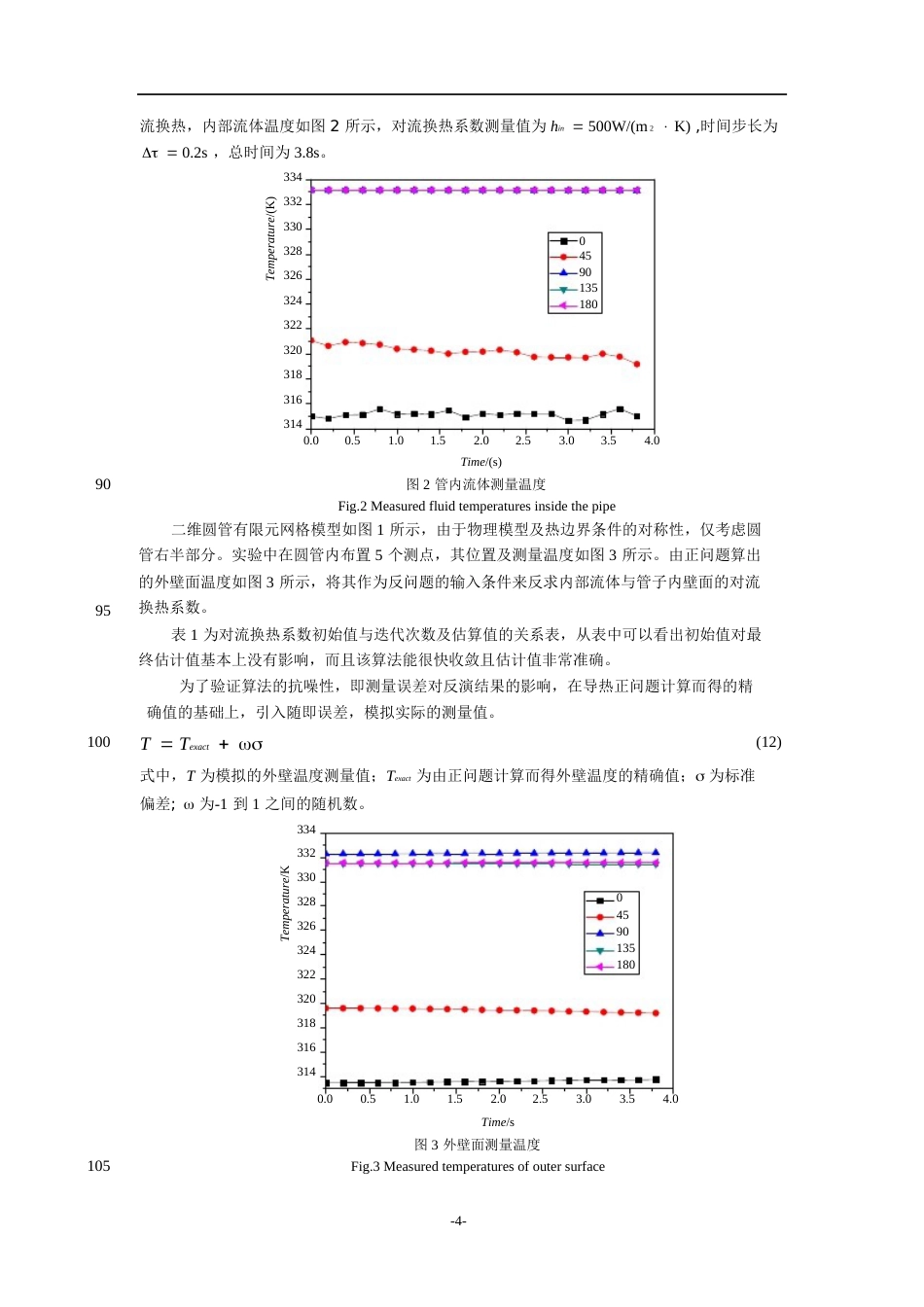
圆管内部流体对流换热系数求解#韩雯雯，卢涛**（北京化工大学机电工程学院，北京100029）5摘要：本文提出了瞬态导热反问题中对流换热系数的一种数值求解方法，得出了敏度计算公式，并应用共轭梯度法进行求解，实现了圆管内部的流体对流换热系数识别。通过典型算例的数值计算，验证了方法的准确性和抗噪性。关键词：工程热物理，瞬态导热，有限元，共轭梯度法，对流换热系数中图分类号：O482.210EstimationofFluidHeatConvectiveCoefficientsofPipeHANWenwen,LUTao(CollegeofMechanicalandElectricalengineering,BeijingUniversityofChemicalTechnology,Beijing100029)1520253035Abstract:Thispaperpresentsanumericalmethodtoidentifyheattransfercoefficientsfortheinverseproblemoftransientheatconduction.Sensitivityformulaearederived,andconjugatetechniqueisemployed.Theestimationoffluidheatconvectivecoefficientsinapipeiscarriedout.Theaccuracyandnoiseresistanceofthemethodareverificatedthroughatypicalexample.Keywords:engineeringthermalphysics;transientheatconduction;finiteelement;conjugategradientmethod;heatconvectivecoefficient0引言管道系统被广泛应用于核电、石油、化工等领域，其中的冷热流体交汇处存在温度波动，会形成热分层现象[1,2]。而热分层现象一般发生在水平管道，可以在冷热流体的交界面观察到循环的温度波动，此波动会使处于此交界面处的管子内部发生热疲劳[3]。近年来，由于核电站事故频发，热疲劳分析引起了广泛的关注。分析受热零件的热疲劳最关键的是确定其温度分布，一旦温度分布确定，便可以确定其他如热流、热应力和热变形等物理场[4]。通常，用实测的方法测量整体的温度场成本很高，在设计中往往采用计算机数值模拟，而数值模拟的关键在于给出接近实际的边界条件。本文讨论在第三类边界条件下的温度场计算中对流换热系数的确定。对流换热系数与换热过程中流体的物理性质、换热表面的形状、部位、表面与流体之间的温差及流体的流速等都有密切关系。目前，求解对流换热系数的方法主要有实验法[5]、特定模型法[6]、试凑法[7]。由于以上几种方法都有各种局限，这就需要我们寻求一种快捷通用的方法。本文通过有限元方法建立热传导正问题模型，用共轭梯度法反求内部流体与圆管内壁面间的对流换热系数，有效避免了各种复杂因素的干扰。由于外壁面的温度易于测量，本文利用外壁面温度构造目标函数，求解二维圆管瞬态导热反问题。数值结果表明，方法可行，并具有相当的通用性。基金项目：基金项目：高等学校博士学科点专项科研基金资助项目(20100010120008)作者简介：韩雯雯，女，博士研究生，主要研究方向：工程热物理通信联系人：卢涛（1975-），男，副教授，主要研究方向：工程热物理.likesurge@sina.com-1-在实际工程中，会面临大量的存在热分层的管道系统，如核电厂里的安注管道等，文中()wf,inf,inw)hTnJ(T)2Tn,m,caln,m,mea1数学模型401主要就管道内的对流换热系数识别进行研究。物理模型如图1所示。根据研究对象的特点，假设管壁导热系数为常数，管内外的对流换热系数也为常数。给定内壁面和外壁面都为第三类边界条件，构成二维导热正问题，其控制方程及边界条件为cT(2T2Tx2y2)(x,y)(1)45(Tn)whf,out(TwTf,out)(x,y)OuterWall（2）TTT0(x,y)(T(x,y)InnerWall(x,y),0(3)(4)这是一个已知外壁面温度数据求解内部流体温度的反问题。该反问题在数学上可以转化为以下泛函变分的最优化问题，即50NMn1m1Tn,m,calTn,m,mea2(5)式中，Tn,m,cal为计算而得的外壁面温度；Tn,m,mea为外壁面的测量温度。M为外壁面测量点数目，N为时间步长数。目标函数的梯度为JhNMn1m1TTn,m,calh（6）55图1物理模型Fig.1Physicalmodel基金项目：高等学校博士学科点专项科研基金资助项目(20100010120008)作者简介：韩雯雯(1985-)，女，博...