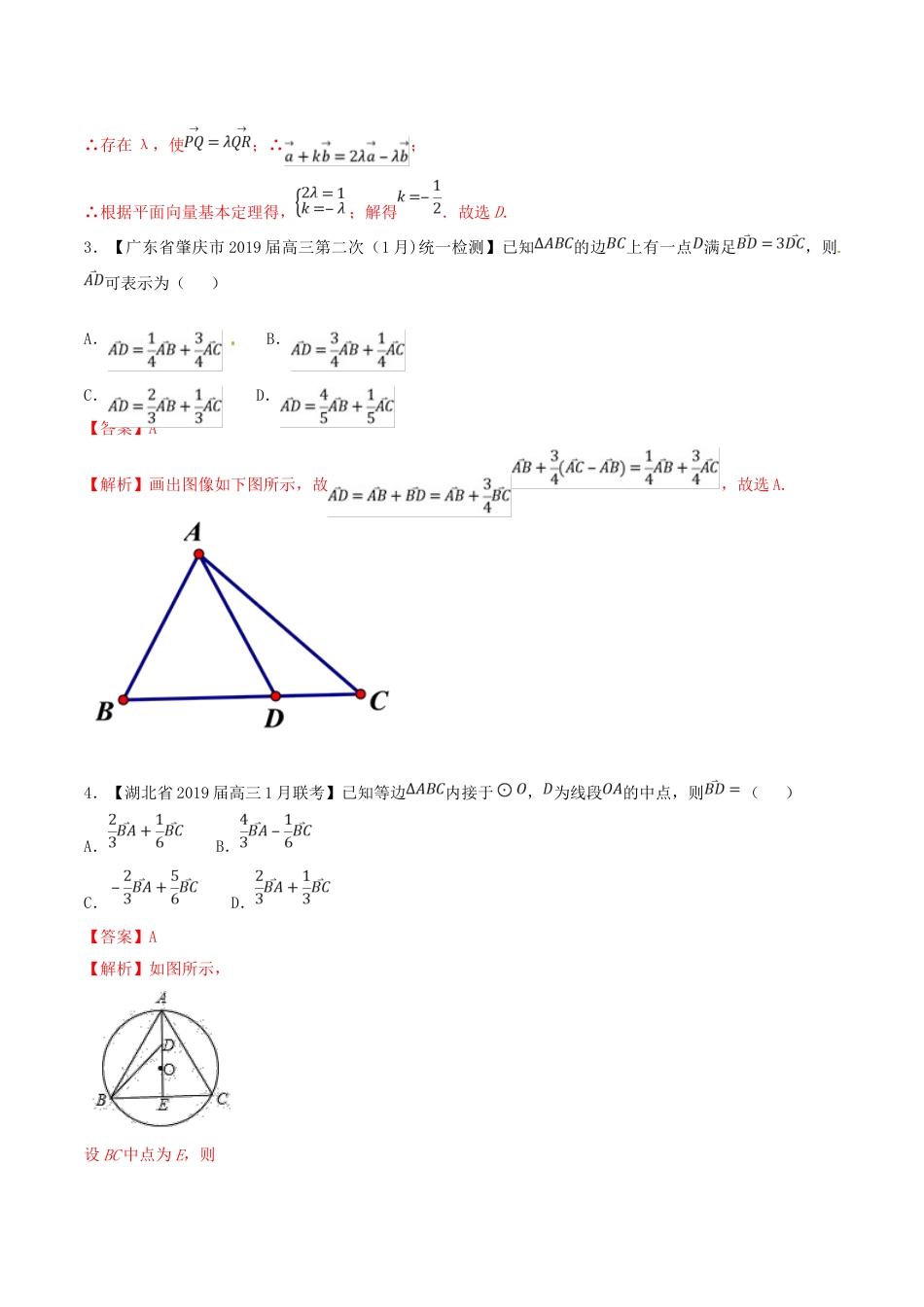
问题14平面向量基本定理的应用问题一、考情分析平面向量问题一直在高中数学中以数学工具的形式出现,它很好的体现了数学知识间的联系与迁移,具体到平面向量基本定理,又在向量这部分知识中占有重要地位,是向量坐标法的基础,是联系几何和代数的桥梁.平面向量的线性运算及应用是高考考查热点,一般以客观题形式出现,难度中等以下．矚慫润厲钐瘗睞枥庑赖賃軔朧碍鳝绢懣硯涛镕頃赎巯驂雞虯从躜鞯烧。二、经验分享1.平面向量线性运算问题的常见类型及解题策略(1)向量加法或减法的几何意义．向量加法和减法均适合三角形法则．(2)求已知向量的和．一般共起点的向量求和用平行四边形法则；求差用三角形法则；求首尾相连向量的和用三角形法则．聞創沟燴鐺險爱氇谴净祸測樅锯鳗鲮詣鋃陉蛮苎覺藍驳驂签拋敘睑绑。【小试牛刀】【山东省曲阜市2018届高三上学期期中】如图,在ABC中,是BN上的一点,若,则实数m的值为（）A.13B.19C.1D.3【答案】B【解析】由可得=,因为,,BPN共线,所以81m9,19m,故选B（四）平面向量基本定理在解析几何中的应用【例4】【2016届安徽省六安一中高三上第五次月考】设双曲线22221xyab的右焦点为F,过点F与x轴垂直的直线l交两渐近线于A,B两点,与双曲线的其中一个交点为P,设坐标原点为O,若(,)mnR,且29mn,则该双曲线的渐近线为（）残骛楼諍锩瀨濟溆塹籟婭骒東戇鳖納们怿碩洒強缦骟飴顢歡窃緞駔蚂。A．34yxB．24yxC．12yxD．13yx【分析】过双曲线的右焦点Fc,0并与x轴垂直的直线:lxc,与渐近线byax的交点坐标为,bc,Acc,bc,Bcc代入向量运算得到点P的坐标,再代入双曲线方程求出离心率,从而渐近线方程可求．酽锕极額閉镇桧猪訣锥顧荭钯詢鳕驄粪讳鱸况閫硯浈颡閿审詔頃緯贾。【点评】解析几何中基本量的计算要注意方程思想的应用和运算的准确性.【小试牛刀】已知是双曲线22221xyab（a0,b0）的左顶点,1F、2F分别为左、右焦点,为双曲线上一点,G是12FF的重心,若1GF�,则双曲线的离心率为（）彈贸摄尔霁毙攬砖卤庑诒尔肤亿鳔简闷鼋缔鋃耧泞蹤頓鍥義锥柽鳗铟。A．2B．3C．4D．与的取值有关【答案】B【解析】因为1GF�,所以1G//F�,所以,即13ac,所以3cea,故选B．五、迁移运用1．【广东省茂名市2019届高三第一次综合测试】在平行四边形中，为上一点，且，记，，则（）A．B．C．D．【答案】B2.【北京市西城区2018-2019学年度第一学期期末】，．若P，Q，R三点共线，则实数k的值为（）謀荞抟箧飆鐸怼类蒋薔點鉍杂篓鳐驱數硯侖葒屜懣勻雏鉚預齒贡缢颔。A．2B．C．D．【答案】D【解析】 是不共线的两个平面向量；∴；即； P，Q，R三点共线；∴与共线；∴存在λ，使；∴；∴根据平面向量基本定理得，；解得．故选D．3．【广东省肇庆市2019届高三第二次（1月)统一检测】已知的边上有一点满足，则可表示为（）A．B．C．D．【答案】A【解析】画出图像如下图所示，故，故选A.4．【湖北省2019届高三1月联考】已知等边内接于，为线段的中点，则（）A．B．C．D．【答案】A【解析】如图所示，设BC中点为E，则（）•．故选：A．7．【2018届广东深圳11月联考】在△ABC中,已知D是AB边上一点,若,则A.13B.23C.13D.23【答案】B【解析】 2ADDB�,∴=23CAAB�==又,∴23。选B.8．【2018届江西省南昌模拟】D是ABC所在平面内一点,,则是点D在ABC内部（不含边界）的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要【答案】B9．【2018届江西新余第四次模拟】如图,已知OAB,若点C满足2ACCB�,,（,R）,则11（）A.13B.23C.29D.92【答案】D【解析】,故选D10．【2018辽宁省沈阳市四校协作体高三年级联合考】在矩形ABCD中,动点P在以点C为圆心且与BD相切的圆上,若,则的最大值为（）厦礴恳蹒骈時盡继價骚卺癩龔长鳏檷譴鋃蠻櫓鑷圣绋閼遞钆悵囅为鹬。A.3B.22C.5D.2【答案】A【解析】如图：以A为原点,以AB,AD所在的直线为x,y轴建立如图所示的坐标系,则A（0,0）,B（1,0）,D（0,2）,C（1,2）,11.【2018届福建省闽侯高三上学期期末】在ABC中,点D满足...