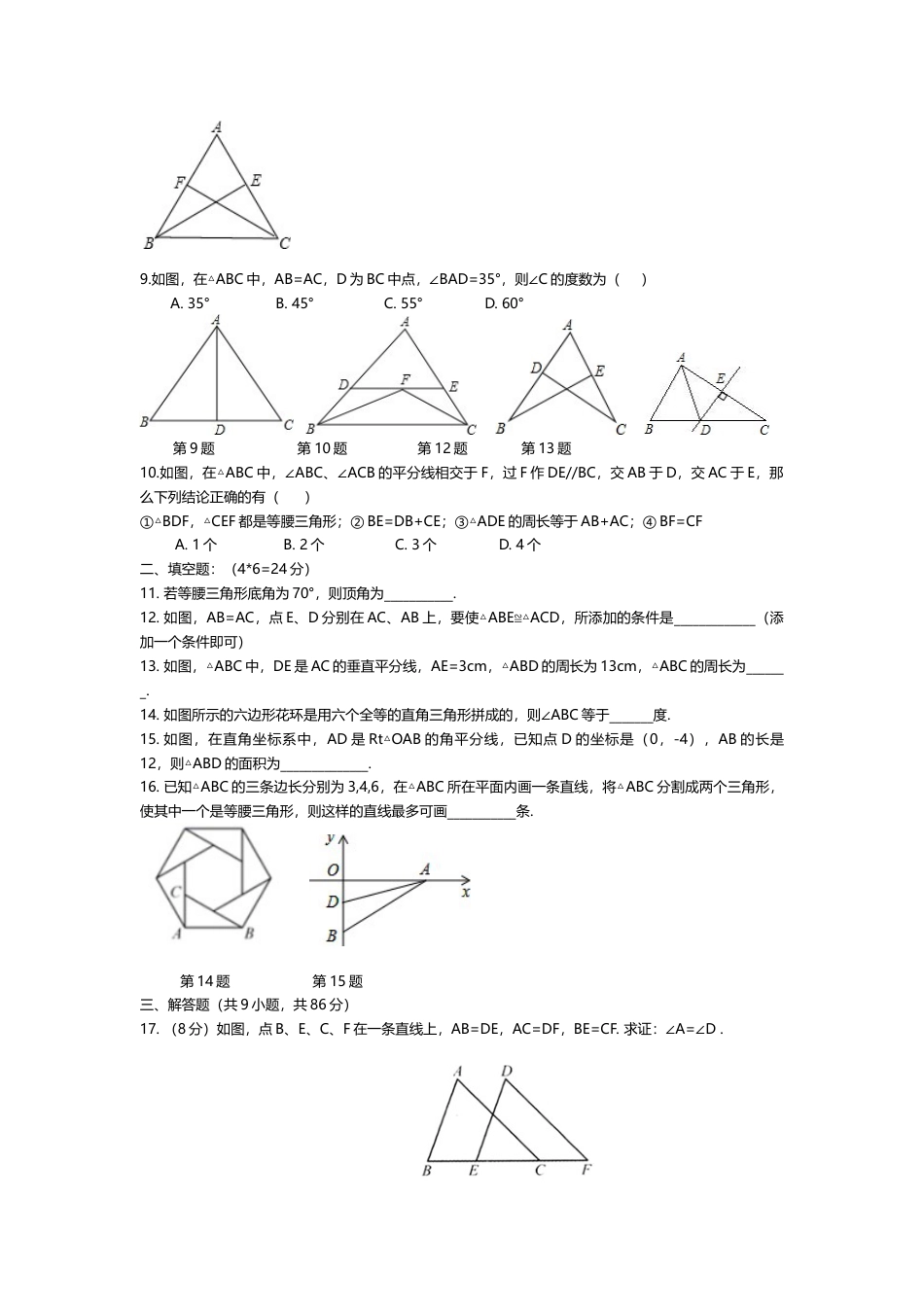
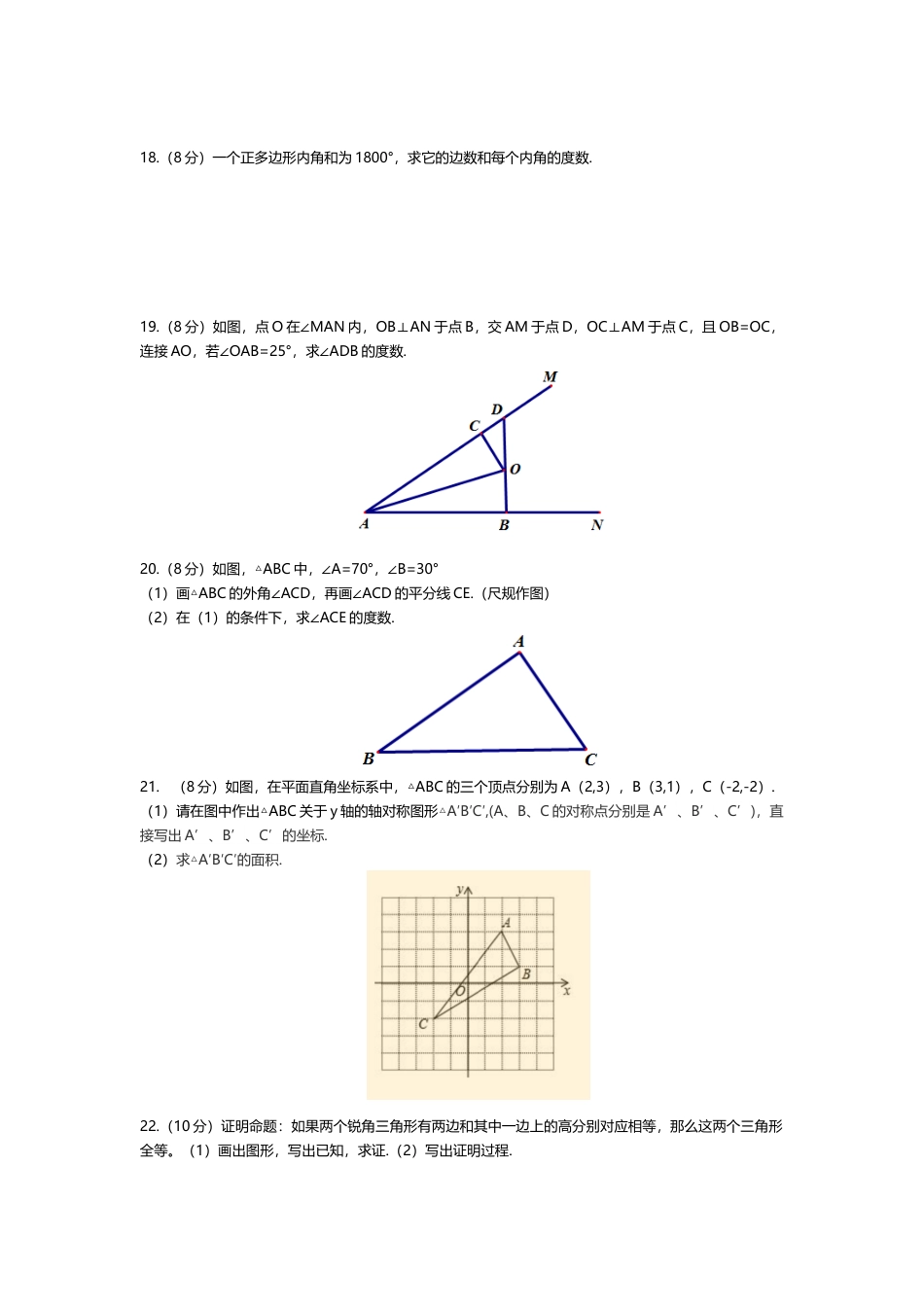
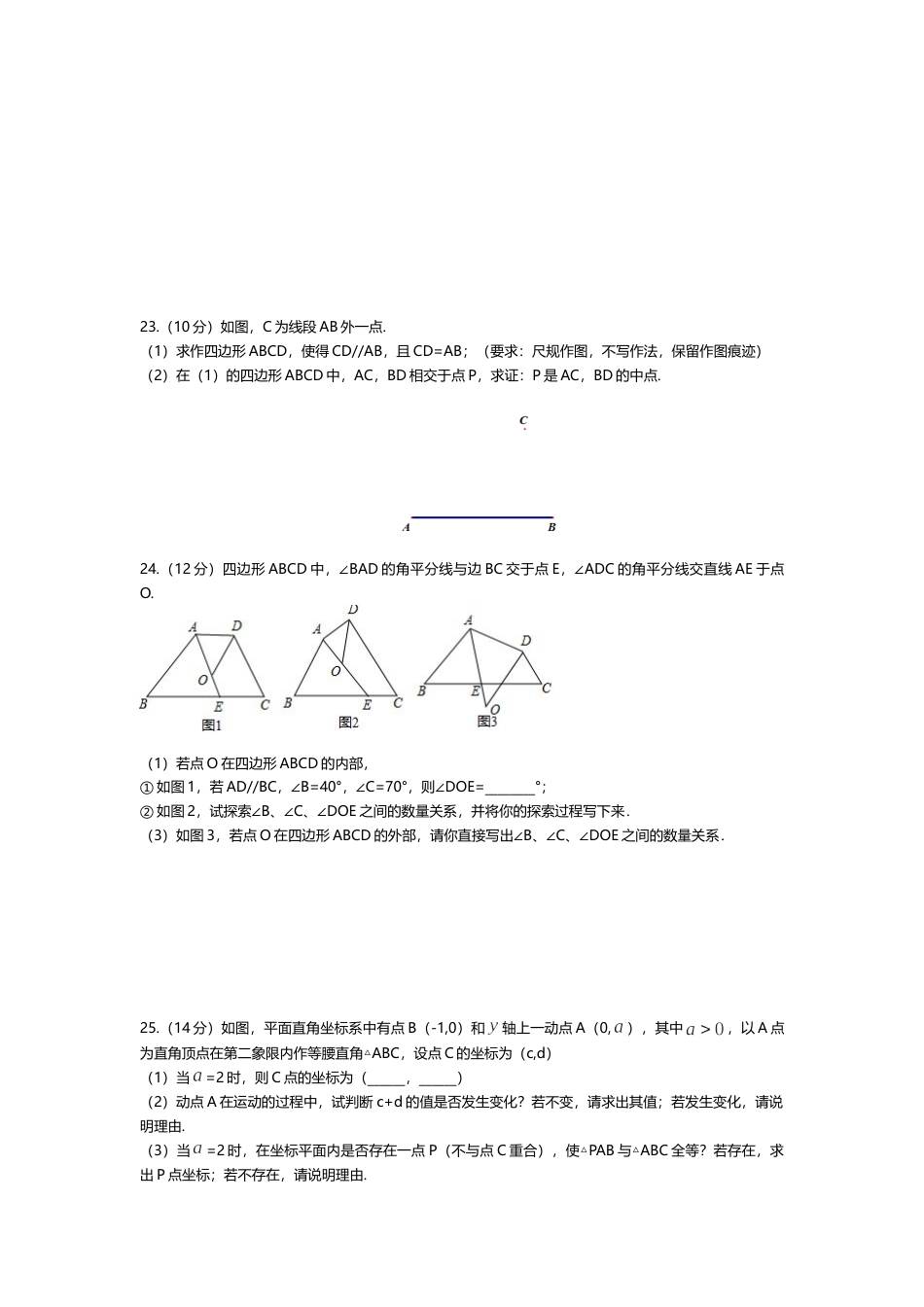
厦门双十中学20~21学年八上第一阶段练习题一、选择题（4*10=40分）1.下列四幅图案中，是轴对称图形的是（）2.下列图形中，不是运用三角形稳定性的是（）A.房屋顶支撑架B.自行车三脚架C.拉闸门D.木门上钉一根木条3.已知图中的两个三角形全等，则∠度数是（）A.50°B.58°C.60°D.72°4.下列各组数中，能作为一个三角形三边边长的是（）A.1,1,2B.1,2,4C.2,3,4D.2,3,55.下面四个图形中，线段BD是△ABC的高的是（）ABCD6.点P（-2,1），那么点P关于轴对称的点P’的坐标是（）A.（-2,1）B.（-2，-1）C.（-1,2）D.（2,1）7.满足下列条件的△ABC中，不是直角三角形的是（）A.∠A=2∠B=3∠CB.∠B+∠A=∠CC.两个内角互余D.∠A：∠B：∠C=2:3:58.如图，在△ABC中，AB=AC，BE、CF是中线，则由（）可得△AFC≌△AEB.A.SSSB.SASC.AASD.ASA9.如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为（）A.35°B.45°C.55°D.60°第9题第10题第12题第13题10.如图，在△ABC中，∠ABC、∠ACB的平分线相交于F，过F作DE//BC，交AB于D，交AC于E，那么下列结论正确的有（）①△BDF，△CEF都是等腰三角形；②BE=DB+CE；③△ADE的周长等于AB+AC；④BF=CFA.1个B.2个C.3个D.4个二、填空题：（4*6=24分）11.若等腰三角形底角为70°，则顶角为___________.12.如图，AB=AC，点E、D分别在AC、AB上，要使△ABE≌△ACD，所添加的条件是_____________（添加一个条件即可）13.如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，△ABC的周长为_______.14.如图所示的六边形花环是用六个全等的直角三角形拼成的，则∠ABC等于_______度.15.如图，在直角坐标系中，AD是Rt△OAB的角平分线，已知点D的坐标是（0，-4），AB的长是12，则△ABD的面积为______________.16.已知△ABC的三条边长分别为3,4,6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中一个是等腰三角形，则这样的直线最多可画___________条.第14题第15题三、解答题（共9小题，共86分）17.（8分）如图，点B、E、C、F在一条直线上，AB=DE，AC=DF，BE=CF.求证：∠A=∠D.18.（8分）一个正多边形内角和为1800°，求它的边数和每个内角的度数.19.（8分）如图，点O在∠MAN内，OB⊥AN于点B，交AM于点D，OC⊥AM于点C，且OB=OC，连接AO，若∠OAB=25°，求∠ADB的度数.20.（8分）如图，△ABC中，∠A=70°，∠B=30°（1）画△ABC的外角∠ACD，再画∠ACD的平分线CE.（尺规作图）（2）在（1）的条件下，求∠ACE的度数.21.（8分）如图，在平面直角坐标系中，△ABC的三个顶点分别为A（2,3），B（3,1），C（-2,-2）.（1）请在图中作出△ABC关于y轴的轴对称图形△A′B′C′,(A、B、C的对称点分别是A’、B’、C’)，直接写出A’、B’、C’的坐标.（2）求△A′B′C′的面积.22.（10分）证明命题：如果两个锐角三角形有两边和其中一边上的高分别对应相等，那么这两个三角形全等。（1）画出图形，写出已知，求证.（2）写出证明过程.23.（10分）如图，C为线段AB外一点.（1）求作四边形ABCD，使得CD//AB，且CD=AB；（要求：尺规作图，不写作法，保留作图痕迹）（2）在（1）的四边形ABCD中，AC，BD相交于点P，求证：P是AC，BD的中点.24.（12分）四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O.（1）若点O在四边形ABCD的内部，①如图1，若AD//BC，∠B=40°，∠C=70°，则∠DOE=________°；②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．（3）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．25.（14分）如图，平面直角坐标系中有点B（-1,0）和轴上一动点A（0,），其中，以A点为直角顶点在第二象限内作等腰直角△ABC，设点C的坐标为（c,d）（1）当=2时，则C点的坐标为（______，______）（2）动点A在运动的过程中，试判断c+d的值是否发生变化？若不变，请求出其值；若发生变化，请说明理由.（3）当=2时，在坐标平面内是否存在一点P（不与点C重合），使△PAB与△ABC全等？若存在，求出P点坐标；若不存在，请说明理由.