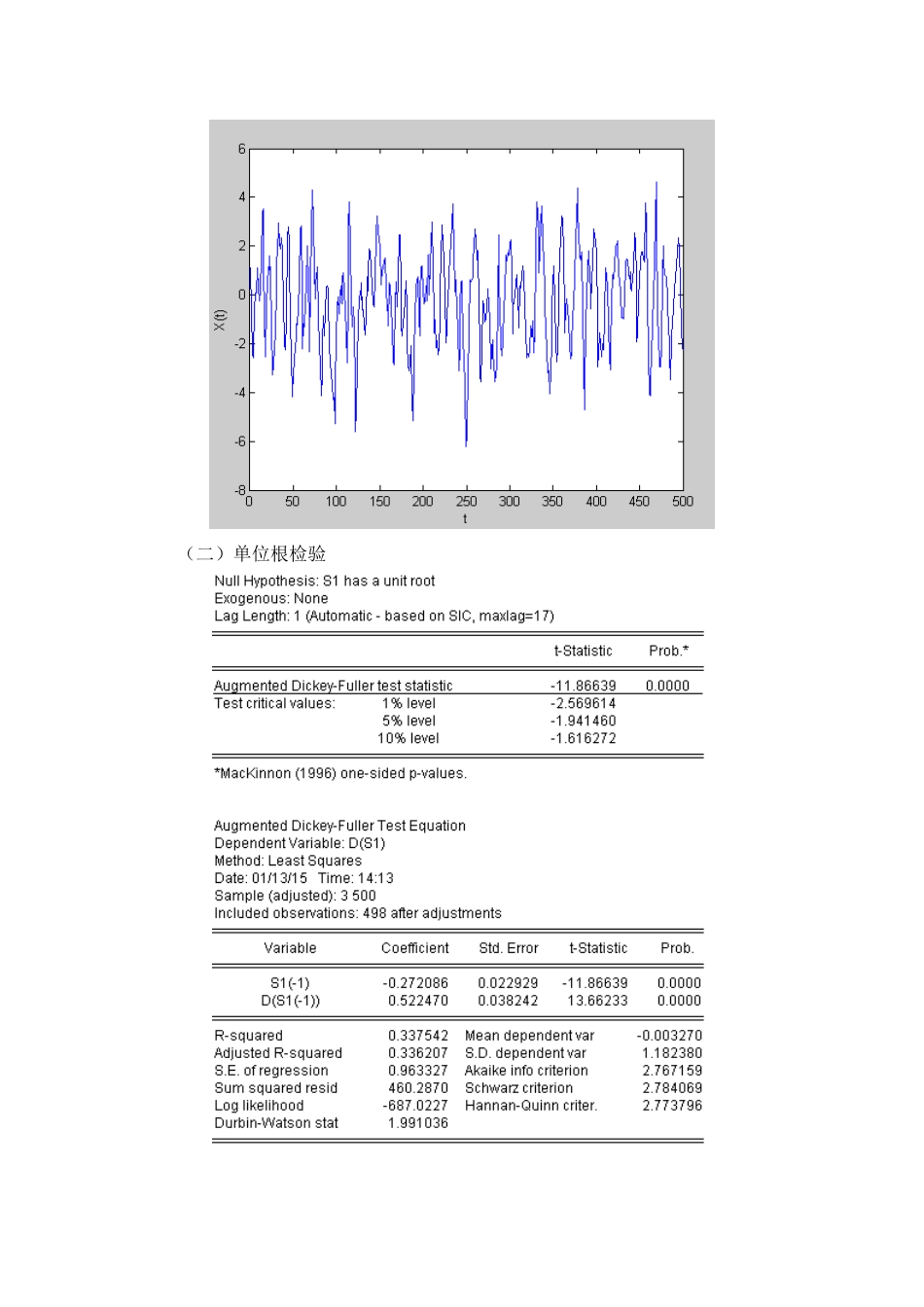
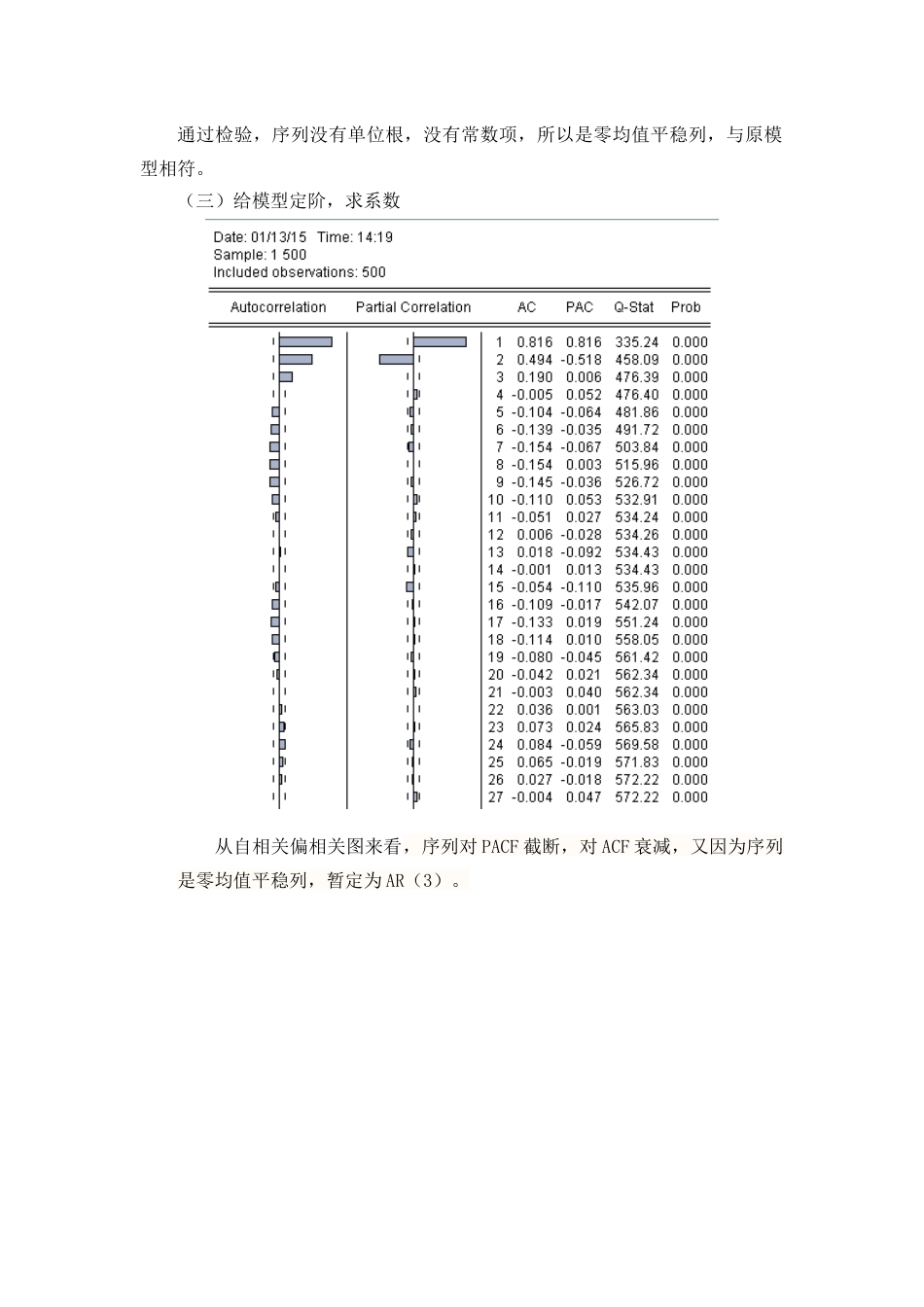
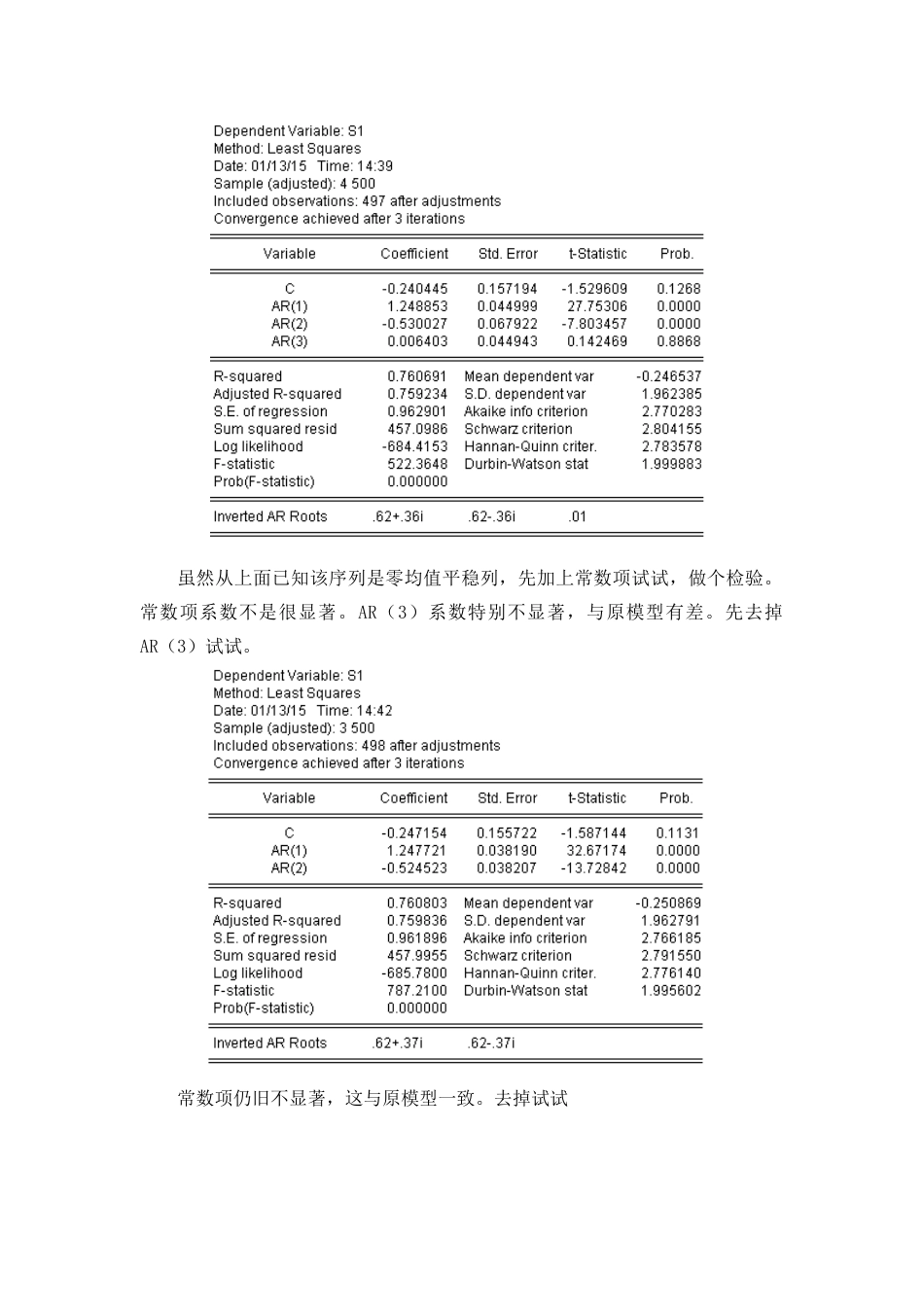
时间序列分析产生序列的matlab代码见最后一、AR(p)序列模型（一）产生数据先用matlab产生AR（4）模型的数据X(t)=a(1)X(t-1)+a(2)X(t-2)+a(3)X(t-3)+a(4)X(t-4)+ε(t),ε(t)服从N(0,σ^2).先选取四个多项式单位根，z1,z2,z3,z4,他们的模都大于一，然后产生相应的多项式，得到一组系数a(1),a(2),a(3),a(4)，满足模型序列是平稳列。>>p=4;>>r=[2,3,4,5];%模型特征多项式的根下面产生该模型相应的数据,500个点；ε(t)服从N(0,c).>>N=500;c=1;>>[X,a]=generate_ar(p,r,N,c);%a是模型系数模型为：X(t)=1.2833*X(t-1)-0.5917*X(t-2)+0.1167*X(t-3)-0.0083*X(t-4)+ε(t)产生的序列图如下：>>plot(X)>>xlabel('t');>>ylabel('X(t)');（二）单位根检验通过检验，序列没有单位根，没有常数项，所以是零均值平稳列，与原模型相符。（三）给模型定阶，求系数从自相关偏相关图来看，序列对PACF截断，对ACF衰减，又因为序列是零均值平稳列，暂定为AR（3）。虽然从上面已知该序列是零均值平稳列，先加上常数项试试，做个检验。常数项系数不是很显著。AR（3）系数特别不显著，与原模型有差。先去掉AR（3）试试。常数项仍旧不显著，这与原模型一致。去掉试试这个模型的R^2与AIC跟别的差不多，各个系数均显著，较别的模型也较为简单，所以先记上面这个模型为模型1,即X(t)=1.250384X(t-1)-0.52247X(t-2)下面再加上AR（3）试试；仍旧不显著，鉴于已知原模型，所以加上AR（4）看看效果记上模型为模型2：X(t)=1.253088X(t-1)-0.5037X(t-2)-0.059X(t-3)+0.0556X(t-4)AR(3),AR(4)仍旧不显著，进而在不知道原模型的情况下，最佳模型应该是模型1：X(t)=1.250384X(t-1)-0.52247X(t-2)拟合图如下：看着效果已经很好了，下面截一小段看看：虽然与原模型不完全一致，但是看拟合效果，已经很不错了，而且从原模型也可以看到，其实AR(3),AR(4)的系数本来就很小，所以建模时没有也正常，如果加上AR(3),AR(4)，也即模型2：X(t)=1.253088X(t-1)-0.5037X(t-2)-0.059X(t-3)+0.0556X(t-4)原模型：X(t)=1.2833X(t-1)-0.5917X(t-2)+0.1167X(t-3)+0.008X(t-4)+ε(t)两个模型在AR(3)上相差较大。下图为模型二的拟合图。上面两个图是模型一和模型二的拟合对比图，两个模型拟合效果差不多，几乎重合，本来模型2中ar(3),ar(4)系数较小，所以影响也不大。看原模型与真值的差异，它是由随机项白噪声产生的：从上面的图可以看到加入随机项后，有时候新建的模型要比原模型的拟合的更好一些，还比原模型简单，也没有滞后效果。再与简单模型X(t)=X(t-1)（记为模型3）做对比感觉模型1要比模型3整体稍微好一点，不过差不太多，而且原模型的AR(1)系数为1.25，相邻的数据相关性较大，所以它们差别不大，用昨日预测今日也是比较合理的，再者，取值范围较小，所以误差也不会太大，差别也不是很大。下面是他们两残差图的比较：系列1是模型1的残差，系列2是模型3的残差，感觉模型1还是要比模型3即简单模型要好一些，但也差不太多。所以最佳模型为：X(t)=1.250384X(t-1)-0.52247X(t-2)。二、ARMA（p,q）模型（一）产生数据ARMA(5,3),即p=5,q=3.先随意产生一组使得模型序列是平稳序列的向量a1,…,a5；b1,…,b3；b0=1;因为要满足是平稳列，需要特征多项式A的根＞1，特征多项式B的根≥1；且它两之间没有相同的根，所以取A的根r1=[1.8,-1.1,-1.6,1.7,-1.4];B的根r2=[1.5,2.1,1.3];>>r1=[1.8,-1.1,-1.6,1.7,-1.4];>>r2=[1.5,2.1,1.3];>>p=5;q=3;>>c=20;%常数项>>N=500;>>[X,a,b]=generate_arma(p,q,r1,r2,N,c);经过多次尝试，尽量选了a(5),b(3)系数较为显著的一个模型，因为上面AR(4)的时候，在建模的时候ar(4)一直不通过，但是原模型有ar(4),只是它的系数很小，这次正好检验一下是不是因为原模型系数小，所以不通过。此外，也尽量选择ar(1)是负的，这样的话用前一天来预测今天效果是不就不好了。而且这次给模型加上了常数项。所以产生的模型为：X(t)=20-1.1046X(t-1)+0.5809X(t-2)+0.7626X(t-3)-0.0796X(t-4)-0.1326X(t-5)-1.9121ε(t-1)+1.1966ε(t-2)-0.2442ε(t-3)+ε(t);>>plot(X)>>title('arma(5,3)')这次这个序列与别比就奇葩多了，波动相当大，...