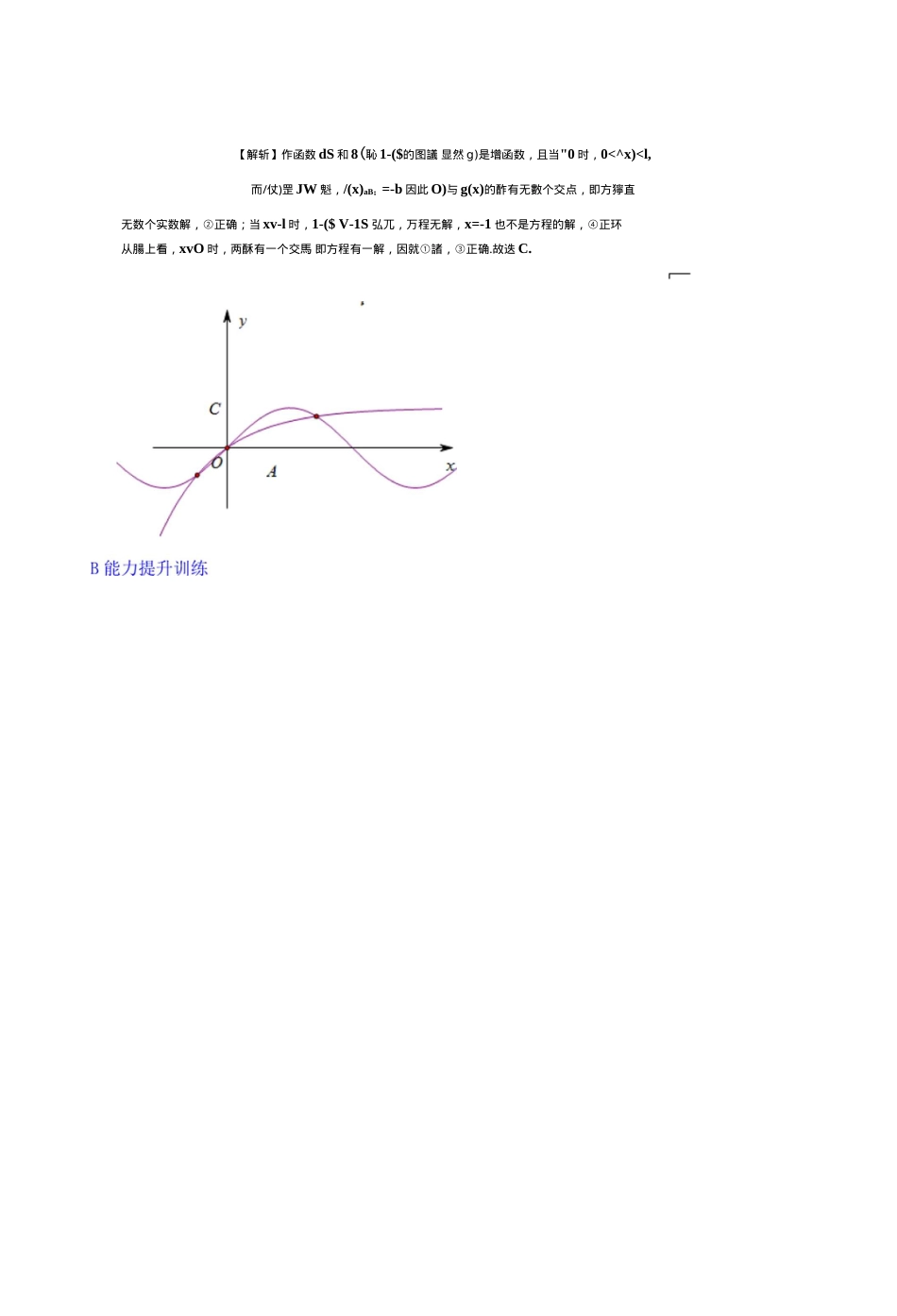
第二章2017年高考数学讲练测【浙江版】【练】函数与基本初等函数I第08节函数与方程A基础巩固训练1.【浙江省嘉兴市第一中学2016届髙三上学期期中考试文数试题解析】关于%的方程ax2-\x\-^a=0有四个不同的解，则实数曰的值可能是()A.—B.—C.1D,242【答案】A【解析】翊分析;若a=2,则2宀中2=0,—无黑若"1,则2-|彳+1二0—4<0,稠，若a=$则*-2恻+1=0,4=0,x=±l,若a则・4闰+1=0,A>0,方程有4个根，成立.故选务a2.【东阳市2015年高三模拟考试理6】若/(x)为奇函数，且勺是=/(%)-eA的一个零点，则-以一定是下列哪个函数的零点(▲)A.y=/(无0+1B.y=/(_x)Q—lc.y=f(x)e'-\D・y-f{-x)ex4-1【答案】A.【解析】依题/(xo)-^=O,对于A,/(—心)£円+1=—/(心)±+l=—±(/(无)—沪)=0,即—兀。是函数y=f(x)ex+l的零点；故选A.3.【2015届辽宁省沈阳市东北育才中学第八次模拟】函数/(x)=lg(x+l)-sin2A：的零点个数为()A.9B.10C.11D.12【答案】D【解析】由题意得：求y=lg(x+l)与y=sin2x交点个数，因为x=±9吋，y=lg10=1,所以当xe[0,9]时，y=lg(兀+1)与y=sin2兀有6个交点；当xe[-9,0)时，y=lg(兀+1)与y=sin2兀有6个交点；所以共有12个交点，选D.4.[2016年第二次全国大联考【浙江卷】理】已知函数/(%)=]x-l~~x^+6x—5,x>0数y=f[f(X)-有6个零点，则实数Cl的取值范围是_________________.【答案】-4<6i<-l【解析】由题可知，函数/S的團象如團所示.令fg-a=f,则要使y=有6个零点，则由/(/)=0,解得20丄5.所以有/(力皿或/(x)m+l或/(乂)=°+5,且oca+l"+5.对于上述方程，要满足条件，则其零点的个数可能为222或口3或330三种可能•若零点个数分别为222,则有一5<a<a+l<a+5<0或一5<a<a+l<0JG+5v4,解得-4U1；若零点个数分别为12.3,由图知，若a+5=4,贝ij^=-l,所以匕+1=0,满足条件，所以。=一1；若c<—5,-5<^+l<O.O<fl+5<l,无解；若零点个数分别为360,则有05<匕+1<1^+%4,无解.综上可知，满足条件的实数。的取值范围罡7血兰-1.5.[2016宁夏银川二中模拟】给定方程：(丄)”+sinx—l=0,给出下列4个结论:2①该方程没有小于0的实数解；②该方程有无数个实数解；③该方程在(-OO,0)内有且只有一个实数根；④若兀是方程的实数根，则x0>-l.其中正确结论的个数是()A.1B.2C.3D.4【答案】C若函【解斩】作函数dS和8(恥1-($的图議显然g)是增函数，且当"0时，0<^x)<l,而/仗)罡JW魁，/(x)aB；=-b因此O)与g(x)的酢有无數个交点，即方獰直无数个实数解，②正确；当xv-l时，1-($V-1S弘兀，万程无解，x=-1也不是方程的解，④正环从腸上看，xvO时，两酥有一个交馬即方程有一解，因就①諸，③正确.故迭C.1.[2016吉林四平模拟】已知函数/(x)=f/1，X>0,若存在X1G(0,+OO),X2G(-OO,0],[x-+l,x<0*■使得fM=/(x2),则西的最小值为()B.logs2C.1D.2A.log23【答案】B【解析】画出函数图象如下图所示，由图可知3"-1=1叭=1跆32・若存在实数b,使函数x>a.g(x)=f(x)—b有两个零点，则实数a的取值范围是()(A)(0,2)(B)(2,+OQ)(C)(2,4)(D)(4,+oo)【答案】C【解析】画出函数y=2\y=x2的图象如下图所示，由图象可知在区间(2,4)符合题意.3.[2016海南中学模拟】若f(x)=\a，X<°，那么f(x)-a的零点个数有()[log“兀，兀>0A.0个B.1个C.2个D.d的值不同时零点的个数不同【答案】B【解析】y=/(x)—a的零点个数等价于方程f{x)=a的根的个数，分别画出心1和0<。v1时/(力的图象，可知无论“为何值，均有1个零点.故选B.当a>l时，函数/(x)的图象如图所示：当0VQV1时，其图彖如下所示:-1-24.[2016海南中学模拟】函数/(x)=y^-sin2x的零点个数为()A.9B.10C.11D.12【答案】C【解析】由/(x)=—-siu2x=0得厉=曲2无，在同一坐标系中分另M乍出函数y=—=siu2x的團象，如下图所示，由图象可知它们共有11个交点，所以函数/(x)=^--sm2xM#点个数为故选C.-4-2-15.[2014天津高考第14题】己知函数/(x)=x2+3x,x\R.若方程/(兀)・a\x-1|=0恰有4个互异的实数根，则实数a的取值范围为________________•【答案】(0,l)U(9,+oo).【解析】方法一：在同一坐标系中画/(%)=%2+3x|和g(x)二ci\x-1|的图彖(如图)，问题转化为/(x)/(耳与g(兀)图象恰有三个交点・把y-a(x-l)代入丁=»+3厂得，+3攵=。(*一学即^+(3—d)x+a=O,...