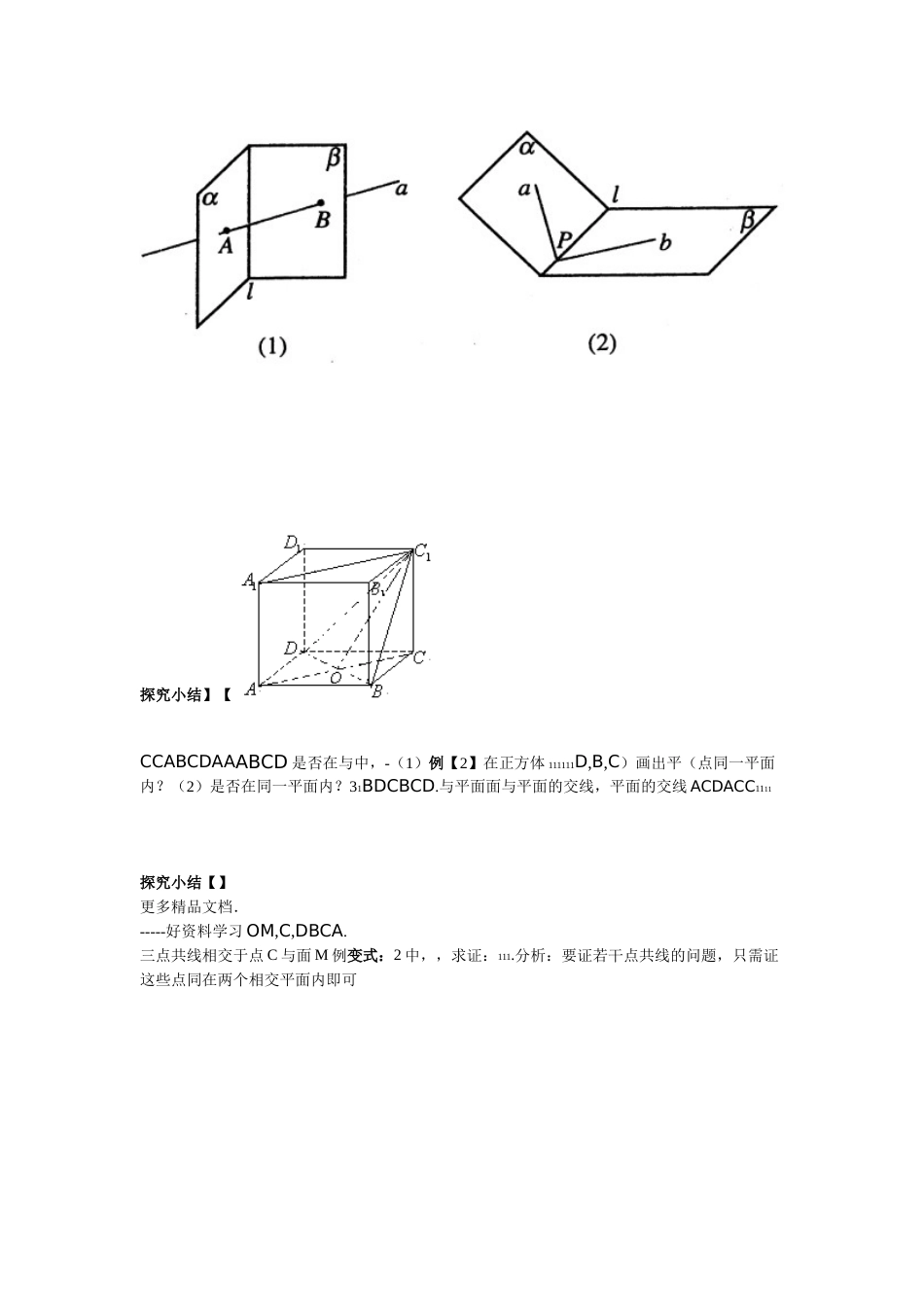
学习-----好资料2.1《空间点、直线、平面之间的位置关系》导学案编写人：朱其山审核人：郭小艳编写时间：2013-05-12.1.1平面第____周高一____班__________合作小组姓名__________【学习目标】1.正确理解平面的概念；掌握平面的基本性质；2.熟练掌握公理1、2、3的三种语言及相互转换；3.会用三个公理证明简单的共点、共线、共面问题；【重点难点】教学重点：公理1、2、3教学难点：三个公理的理解【学法指导】注意观察教室中的点、线、面，你会有很多的收获！预习案阅读课本P40-43，完成下面预习案一、知识梳理1．平面概述（1）平面的两个特征：①无限延展②没有厚度（2）平面的画法：（3）平面的表示：??内，记作，点B不在平面平面可以看成点的集合，点A在平面内，记作2．三个公理公理1：用数学符号表示为：图形语言：公理2：用数学符号表示为：图形语言：公理3：用数学符号表示为：图形语言：3.公理2的三条推论：推论1经过一条直线和这条直线外的一点，有且只有一个平面；更多精品文档．学习-----好资料推论2经过两条相交直线，有且只有一个平面；推论3经过两条平行直线，有且只有一个平面.二、问题导学为什么要学习三个公理？三个公理的作用是什么？三、预习自测1．下列推断中，错误的是（）.?????????A．B．??B?A?l,A?l,B?l,ABB??,A?,B??,A?、、??????重合BD．C，且A．C不共线?l?l?A,A?,?CA,B,??,A,B,C2．下列结论中，错误的是（）A．经过三点确定一个平面B．经过一条直线和这条直线外一点确定一个平面C．经过两条相交直线确定一个平面D．经过两条平行直线确定一个平面3．用符号表示下列语句，并画出相应的图形：?a外的一点）直线M;经过平面（1??a内;（2）直线内，又在平面既在平面．如图，试根据下列要求，把被遮挡的部分改为虚线：4?没有被平面遮挡；（1）AB?被平面遮挡（2）AB【疑惑之处】探究案.如图，用符号表示下图图形中点、直线、平面之间的位置关系【例1】探究小结】【CCABCDAAABCD是否在与中，-（1）例【2】在正方体111111D,B,C）画出平（点同一平面内？（2）是否在同一平面内？31BDCBCD.与平面面与平面的交线，平面的交线ACDACC1111探究小结【】更多精品文档．-----好资料学习OM,C,DBCA.三点共线相交于点C与面M例变式：2中，，求证：111.分析：要证若干点共线的问题，只需证这些点同在两个相交平面内即可??,Q,R,Q,RPPABC?在同外，它的三边所在的直线分别交面,在平面【例3】已知于求证：.一条直线上ACBRPQ?【探究小结】课堂检测.）1．下列说法中正确的是（空间两两相交的三条直线确定一个平面B.A.空间不同的三点确定一个平面空间有三个角为直角的四边形一定是平面图形C.和同一条直线相交的三条平行直线一定在同一平面内D..2．给出下列说法，其中说法正确的序号依次是梯形的四个顶点共面；①三条平行直线共面；②有三个公共点的两个平面重合；③每两条都相交并且交点全部不同的四条直线共面.④.．已知空间四点中无任何三点共线，那么这四点可以确定平面的个数是3?a表示直线，表示平面）4．下面四个叙述语（其中A,B表示点，?????,B?ABA?,；①????AB,?A?B,?②；?????a,aA,?A；③??a?,?AA?,a?.④其中叙述方式和推理都正确的序号是更多精品文档．学习-----好资料a的正方体ABCD-ABCD中M,N分别是AA，DC的中点，过点D5．在棱长为，M，N三点1111111l，相交于直线BCD的平面与正方体的下底面A1111l；）画出直线（1lAB?P，求PB（2）设的长；111l的距离到.3）求D（1课后检测1．下列推断中，错误的是（）.???A．??lB?l,BA?l,A??,??????B．AB?,BA??,A??,B???C．?l??A,A?l????重合不共线A、BD．、C，且,?BA,,CA,B,C??,2．E、F、G、H是三棱锥A-BCD棱AB、AD、CD、CB上的点，延长EF、HG交于P，则点P（）.A.一定在直线AC上B.一定在直线BD上C.只在平面BCD内D.只在平面ABD内3．用一个平面截一个正方体，其截面是一个多边形，则这个多边形边数最多是（）.A.三B.四C.六D.八4．下列说法中正确的是（）.A.空间不同的三点确定一个平面B.空间两两相交的三条直线确定一个平面C.空间有三个角为直角的四边形一定是平面图D.和同一条直线相交的三条平行直线一定在同一平面内5.两个平面若有三个公共点，则...