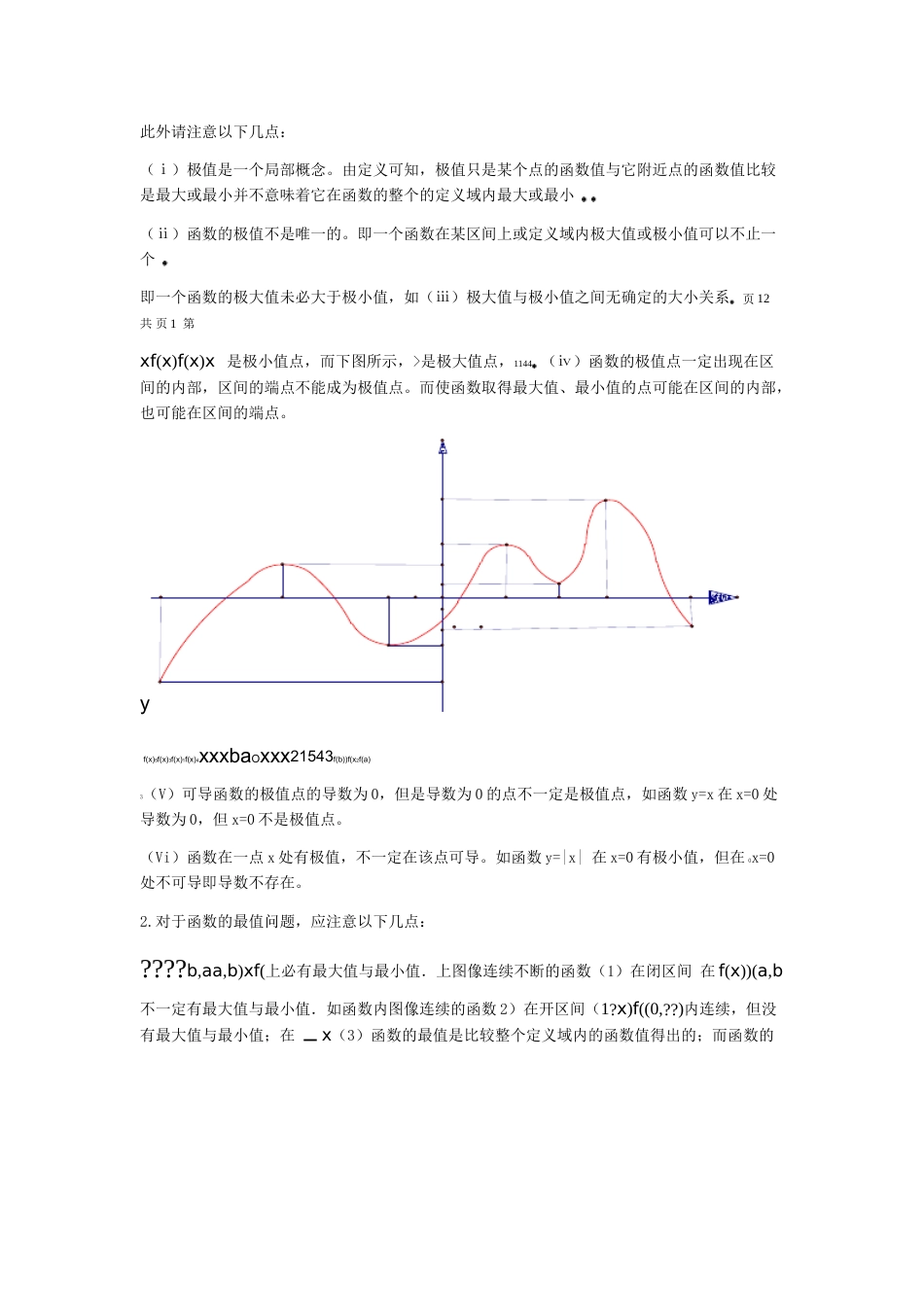
§3.3利用导数研究函数的极值和最值知识要点梳理一.函数的极值1.函数极值定义一般地，设函数f(x)在点x附近有定义，如果对x附近的所有的点，都有f(x)＜f(x)，000就说f(x)是函数f(x)的一个极大值，记作y=f(x)，x是极大值点。000极大值如果对x附近的所有的点，都有f(x)＞f(x).就说f(x)是函数f(x)的一个极小值，记作y000=f(x)，x是极小值点。极大值与极小值统称为极值00极小值2.判别f(x)是极大、极小值的方法:0?(x)?f0xxxf(x)f(x)的极值点，若是满足的两侧的导数异号，则，且在0000?xxx)f(f(x(x)f)的极大值点，是是极值，并且如果两侧满足“左正右负”在，则000?xxf)(x)f(x)f((x)xf的极小值点，是极大值；是两侧满足“左负右正”，在则如果0000是极小值.3.求可导函数f(x)的极值的步骤:(1)确定函数的定义区间，求导数f′(x)(2)求方程f′(x)=0的根检查.的点，顺次将函数的定义域分成若干小开区间，并列成表格(3)用函数的导数为0如果左负在这个根处取得极大值；x)那么)在方程根左右的值的符号，如果左正右负，f(f′(x在这个根处无极值x)x)在这个根处取得极小值；如果左右不改变符号，那么f(右正，那么f(函数的最大值与最小值二.1.函数的最大值与最小值：????b,ba,a)(xf上必有最大值与最小值．在在闭区间上图像连续不断的函数??b,a)xf(上图在闭区间在在（a,b2.利用导数求函数的最值步骤:设函数）内可导，??b,a)f(x上的最大值与最小值的步骤如下：在像连续不断，求函数f(x)(a,b)内的极值；⑴求在??b,a)(b)f(xfaf(fx)()上的最值，其中最大⑵将比较，、的各极值与得出函数在的一个是最大值，最小的一个是最小值。疑难点、易错点剖析1由极值的定义可知，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值。此外请注意以下几点：（ⅰ）极值是一个局部概念。由定义可知，极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小（ⅱ）函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个即一个函数的极大值未必大于极小值，如（ⅲ）极大值与极小值之间无确定的大小关系页12共页1第xf(x)f(x)x是极小值点，而下图所示，>是极大值点，1144（ⅳ）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部，也可能在区间的端点。yf(x)5f(x)3f(x)1f(x)4xxxbaOxxx21543f(b))f(x2f(a)3（V）可导函数的极值点的导数为0，但是导数为0的点不一定是极值点，如函数y=x在x=0处导数为0，但x=0不是极值点。（Vi）函数在一点x处有极值，不一定在该点可导。如函数y=|x|在x=0有极小值，但在0x=0处不可导即导数不存在。2.对于函数的最值问题，应注意以下几点：????b,aa,b)xf(上必有最大值与最小值．上图像连续不断的函数（1）在闭区间在f(x))(a,b不一定有最大值与最小值．如函数内图像连续的函数2）在开区间（1?x)f((0,??)内连续，但没有最大值与最小值；在x（3）函数的最值是比较整个定义域内的函数值得出的；而函数的极值是比较极值点附近函数值得出的．??b,a)f(x上的图像连续）函数4在闭区间（??ba,)(xf上有最大值与最小值在闭区间不断，是数函．如非必要条件的充分条件而0x?x?1但x???1,???1,1??)f(x上有最大在?0?0,x??，但其图-2），最小值是值，最小值，（最大值是0像却不是连续不断的（如右图）。而函数的极值可能不止一个，最小值最多各有一个，函数在其定义区间上的最大值、(5)也可能没有一个。上递增，则在闭区间[a,b]f(x)（6）若函数只有一个极值，则必为最值。若函数f(x)页12共页2第f(x)?f(b))(bx)?ff(x)?f(a)f(，[a,b]上递减，则；若函数f(x)，在闭区间minmaxminf(x)?f(a)。max直击考点考点一求含字母参数的函数的极值??23?)?Rcx(xx?x?bxf?(x))?f(x)?f(xg是奇06安徽卷）设函数，已知考例1.（函数。cb的值。、（Ⅰ）求g(x)的单调区间与极值。（Ⅱ）求f'(x),再利用奇函数定义即可求出b,c思路分析：先求出的值，再利用导数这一工具，可求出函数的单调区间及极值????232??2bx?xxc?x??bx3?cxffx。从而解析：（Ⅰ） ，∴32232??(c?2b)x)cx??(b??fx(x)?3)?bxx?...