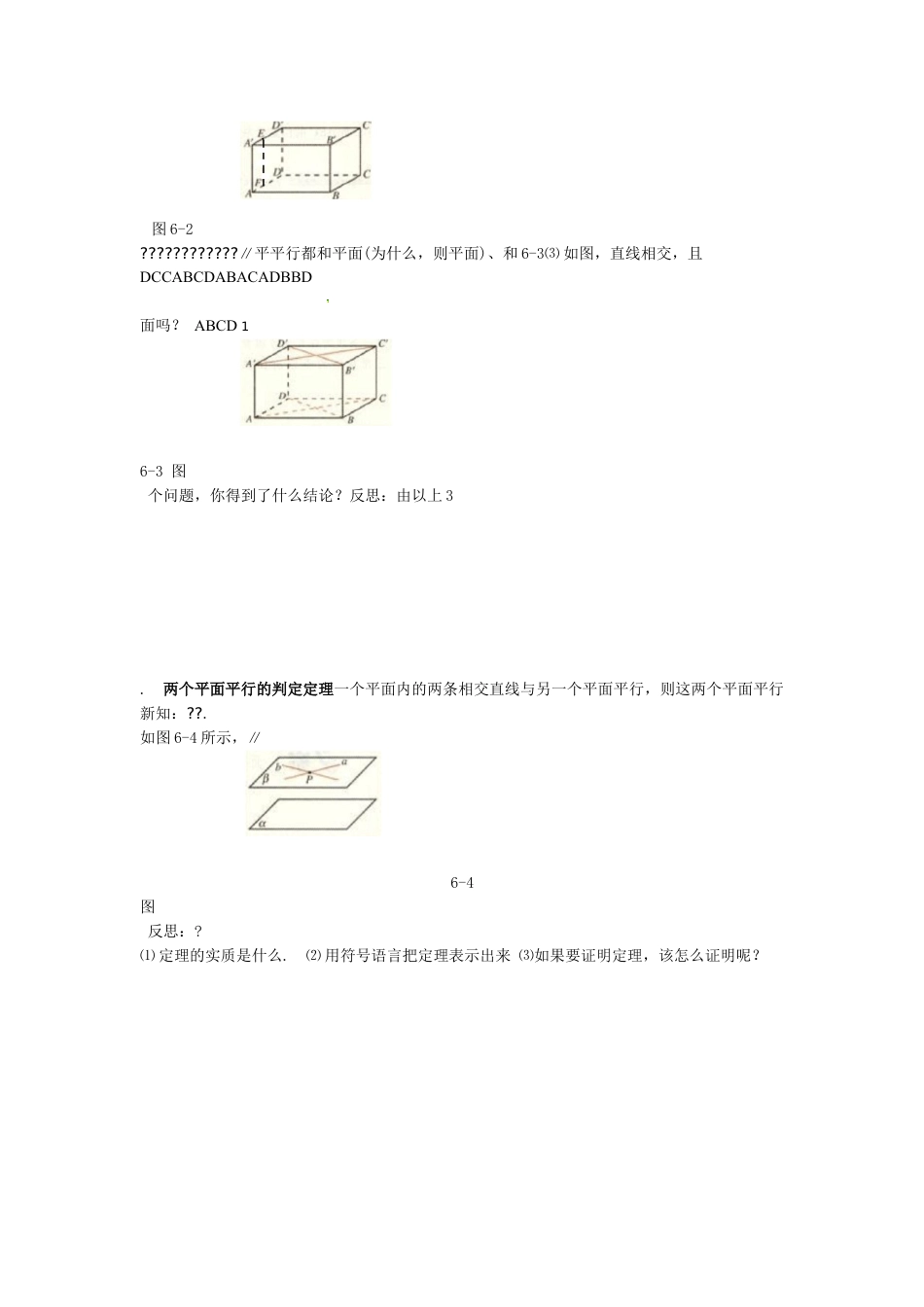
平面与平面平行的判定§2.2.2学习目标：1.能借助于长方体模型讨论直线与平面、平面与平面的平行问题；2.理解和掌握两个平面平行的判定定理及其运用；3.进一步体会转化的数学思想.学习重点:掌握平面与平面平行的判定定理.学习难点:理解平面与平面平行的判定定理.课前预习PP，找出疑惑之处）（预习教材~5756复习1：直线与平面平行的判定定理是______________________________________________________.复习2：两个平面的位置关系有___种，分别为_______和_______.讨论：两个平面平行的定义是两个平面没有公共点,怎样证明两个平面没有公共点呢?你觉得好证吗?课内探究探究：两个平面平行的判定定理问题1：平面可以看作是由直线构成的.若一平面内的所有直线都与另一个平面平行，则这两个平面平行吗？由此你可以得到什么结论？结论：两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.问题2：一个平面内所有直线都平行于另外一个平面好证明吗？能否只证明一个平面内若干条直线和另外一个平面平行，那么这两个平面就平行呢？试试：在长方体中，回答下列问题??????????吗？∥面∥面,，则面⑴如图6-1，CCCCBBBBBAABAAB?面AABAA图6-1??????????吗？6-2，∥，∥，则，∥∥⑵如图EFEFAAAAD面ADCC面DDADD面DCC面DCC图6-2????????????∥平平行都和平面(为什么，则平面)、和6-3⑶如图，直线相交，且DCCABCDABACADBBD面吗？ABCD16-3图个问题，你得到了什么结论？反思：由以上3.两个平面平行的判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行新知：??.如图6-4所示，∥6-4图反思：?⑴定理的实质是什么.⑵用符号语言把定理表示出来⑶如果要证明定理，该怎么证明呢？.，求证：平面∥已知正方体，如图6-51例DABDDCBAABCD?CB111111126-5图??，与是两条异面直线，平面过，与平行，平面平行，过例2如图6-6，已知ba,bbaa??求证：平面∥平面b?a?6-6图.小结：证明面面平行，只需证明线线平行，而且这两条直线必须是相交直线动手试试※????????，∥分别是棱6-7，正方体中，，，的中点，求证：平面练.如图F,M,NE,AMNCDBCDAAB.平面EFDB?DF?CN?AE?BMDCAB6-7图当堂检测??.平面与平面）平行的条件可以是（1.??A.平行内有无穷多条直线都与????和直线B.与都平行，且不在内,a????直线∥,且∥,C.直线,?bba?a??内的任何直线都与D.平行??.）2.经过平面外的一条直线且与平面平行的平面（a有且只有一个A.B.不存在D.C.至多有一个至少有一个3??.）3.设有不同的直线，及不同的平面，给出的三个命题中正确命题的个数是（、ba,??????????.∥∥∥,∥②若,则∥∥③若,,∥则,则∥①若,?abbaaaaa个个A.0个B.1个C.2D.3________________.条，则这两个平面的位置关系是4.如果两个平面分别经过两条平行线中的一_______________.则这两平面的位置关系是5.若两个平面都平行于两条异面直线中的每一条,课后反思的判定定理及应用；1.平面与平面平行.转化思想的运用2.知识拓展判定平面与平面平行通常有5种方法⑴根据两平面平行的定义(常用反证法)；⑵根据两平面平行的判定定理；⑷两个平面同时平行于第三个平面，则这两个平面平行⑶垂直于同一条直线的两个平面平行(以后学习)；(平行的传递性)；判定定理的推⑸一个平面内的两条相交直线分别平行于另外一个平面内的两条直线，则这两个平面平行().论课后训练a）a平行的（1.直线∥平面α，平面α内有无数条直线交于一点，那么这无数条直线中与直线）至多有一条（B（A）至少有一条）不可能有（D（C）有且只有一条??????,,b?c,ab,c中，a?,的则两个平面已知三条互相平行的直线,,2..位置关系是,那么这两个平面的位置关系是3.如果两个平面分别平行于第三个平面BDDDBCDABCD?A的位置关系，并给出证明。E4、正方体中，为与平面的中点，判断AEC111111DC11EAB11CD???,5°+体中，,°如图6-8，在几何1804??1802AABC?BC??3??1?AB???.∥平面求证：平面CABCAB6-8图4??????、求证：面，、分别是∥、6-96.如图..的重心、C?BCA?PBCPCABPAB?AABC面6-9图5