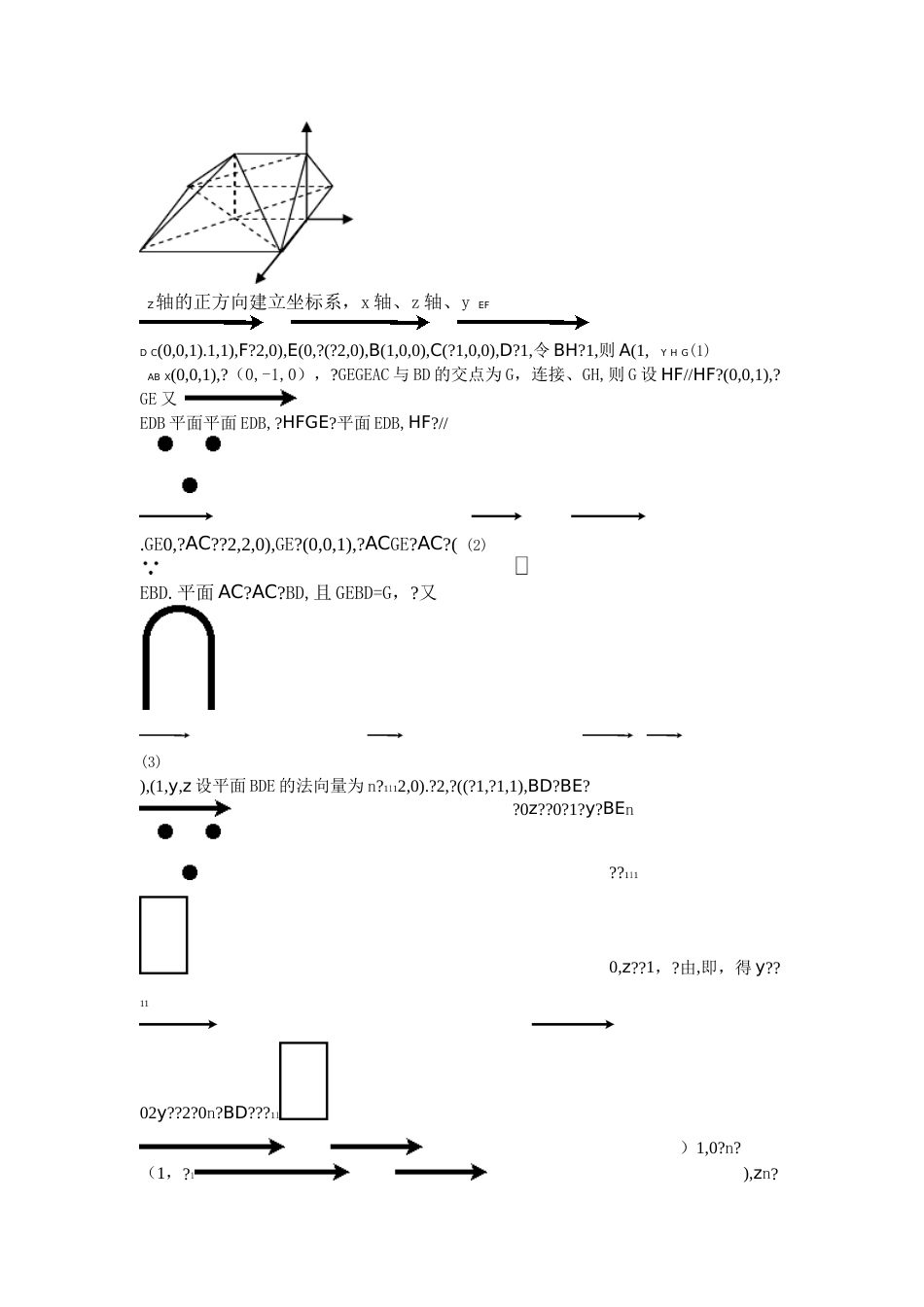
精品文档专题四：立体几何第三讲空间向量与立体几何【最新考纲透析】1．空间向量及其运算（1）了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的线性运算及其坐标表示。（2）掌握空间向量的线性运算及其坐标表示。（3）掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直。2．空间向量的应用（1）理解直线的方向向量与平面的法向量。（2）能用向量语言表述直线与直线，直线与平面，平面与平面的垂直、平行关系。（3）能用向量方法证明有关直线和平面位置关系的一些定理（包括三垂线定理）。（4）能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究立体几何问题中的应用。【核心要点突破】要点考向1：利用空间向量证明空间位置关系考情聚焦：1．平行与垂直是空间关系中最重要的位置关系，也是每年的必考内容，利用空间向量判断空间位置关系更是近几年高考题的新亮点。2．题型灵活多样，难度为中档题，且常考常新。考向链接：1．空间中线面的平行与垂直是立体几何中经常考查的一个重要内容，一方面考查学生的空间想象能力和逻辑推理能力；另一个方面考查“向量法”的应用。2．空间中线面的平行与垂直的证明有两个思路：一是利用相应的判定定理和性质定理去解决；二是利用空间向量来论证。ABCDEFABCDEF∥）如图，在多面体是正方形，中，四边形（例1：2010·安徽高考理科·Ｔ18?BFC?90?BF?FCBCABEF?2FBEF?ABH的中点。，，为，，，FHEDB；(1)求证：∥平面AC?EDB；平面(2)求证：B?DE?C的大小。(3)求二面角【命题立意】本题主要考查了空间几何体的线面平行、线面垂直的证明、二面角的求解的问题，考查精品文档．精品文档了考生的空间想象能力、推理论证能力和运算求解能力。【思路点拨】可以采用综合法证明，亦可采用向量法证明。【规范解答】，BBCFB??AB?FB,且EF?ABCD为正方形，?AB?BC,又FB,EF//AB,四边形,FH?FBC,AB??AB?平面,?中点，?FHBC又BF?FC,H为BC,BBC?且AB.FH??平面ABC的方向为HF、GH、如图，以H为坐标原点，分别以HBZ轴的正方向建立坐标系，x轴、z轴、yEFDC(0,0,1).1,1),F?2,0),E(0,?(?2,0),B(1,0,0),C(?1,0,0),D?1,令BH?1,则A(1,YHG(1)ABX(0,0,1),?（0,-1,0），?GEGEAC与BD的交点为G，连接、GH,则G设HF//HF?(0,0,1),?GE又EDB平面平面EDB,?HFGE?平面EDB,HF?//.GE0,?AC??2,2,0),GE?(0,0,1),?ACGE?AC?((2)EBD.平面AC?AC?BD,且GEBD=G，?又(3)),(1,y,z设平面BDE的法向量为n?1112,0).?2,?((?1,?1,1),BD?BE??0z??0?1?y?BEn??1110,z??1，?由,即，得y??1102y??2?0n?BD???11）1,0?n?（1，?1),zn?(1,y,设平面CDE的法向量为2221,1).?2,0),CE?(1,CD?(0,??00CDn?y???221,?y?0，z?，得由,即??220zy??1?0CEn????222）0,-1?（n?1，2nn1121,??n??,?cos?n212|n||n|2221。为60,nn,??60即二面角B-DE-C??21【方法技巧】1、证明线面平行通常转化为证明直线与平面内的一条直线平行；2、证明线面垂直通常转化为证明直线与平面内的两条相交直线垂直；精品文档．精品文档3、确定二面角的大小，可以先构造二面角的平面角，然后转化到一个合适的三角形中进行求解。4、以上立体几何中的常见问题，也可以采用向量法建立空间直角坐标系，转化为向量问题进行求解证明。应用向量法解题，思路简单，易于操作，推荐使用。要点考向2：利用空间向量求线线角、线面角考情聚焦：1．线线角、线面角是高考命题的重点内容，几乎每年都考。2．在各类题型中均可出现，特别以解答题为主，属于低、中档题。考向链接：1．利用空间向量求两异面直线所成的角,直线与平面所成的角的方法及公式为:）异面直线所成角（1的方向向量，则设分别为异面直线）线面角（2nl是平面的法向量，则的方向向量，设是直线2．运用空间向量坐标运算求空间角的一般步骤为：（1）建立恰当的空间直角坐标。（2）求出相关点的坐标。（3）写出向量坐标。（4）结合公式进行论证、计算。（5）转化为几何结论。1AB，PA=AC=，N为PA⊥ABC，AB⊥AC19例2：（2010·辽宁高考理科·Ｔ）已知三棱锥P－ABC中，2.PB,BC的中点AB=4AN,M,S分别为AB上一点，⊥SN；（Ⅰ）证明：CM.CMN所成角...