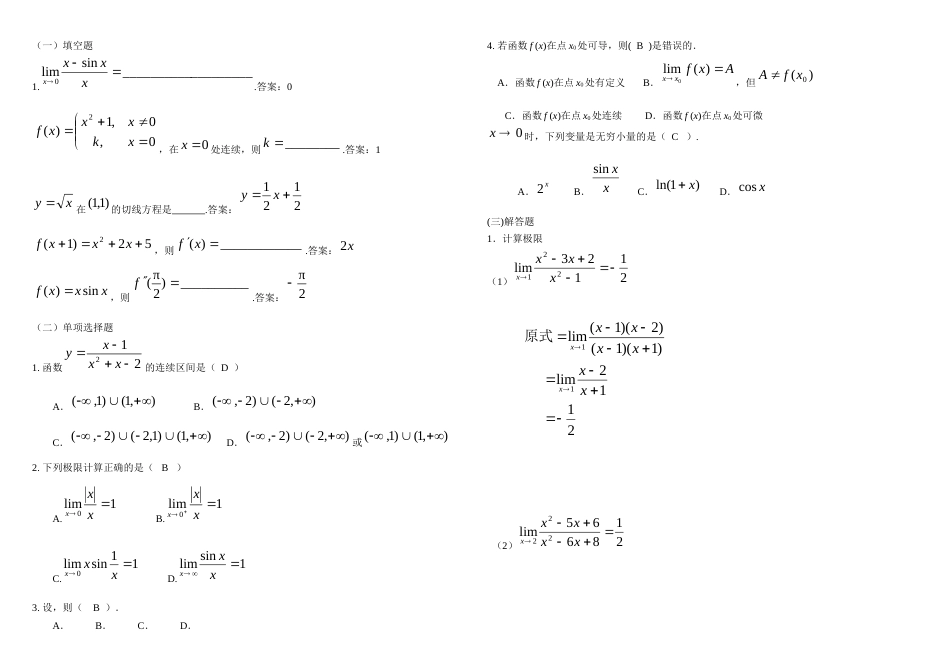
（一）填空题1.___________________sinlim0xxxx.答案：00,0,1)(2xkxxxf，在x0处连续，则k________.答案：1xy在)1,1(的切线方程是.答案：2121xy52)1(2xxxf，则____________()fx.答案：x2xxfxsin()，则__________2)(πf.答案：2π（二）单项选择题1.函数212xxxy的连续区间是（D）A．),1()1,(B．),2(,2)(C．),1()1,2(,2)(D．),2(,2)(或),1()1,(2.下列极限计算正确的是（B）A.1lim0xxxB.1lim0xxxC.1sin1lim0xxxD.1limsinxxx3.设，则（B）．A．B．C．D．4.若函数f(x)在点x0处可导，则(B)是错误的．A．函数f(x)在点x0处有定义B．Axfxx()lim0，但)(0xfAC．函数f(x)在点x0处连续D．函数f(x)在点x0处可微x0时，下列变量是无穷小量的是（C）.A．x2B．xxsinC．)ln(1xD．xcos(三)解答题1．计算极限（1）21123lim221xxxx2112lim)11)((2)1)((lim11xxxxxxxx原式（2）218665lim222xxxxx原式=-2)(x-4)(x(x-2)(x-3)lim2x2143lim2xxx（3）2111lim0xxx原式=)11()11)(1(1lim0xxxxx=111lim0xx=21（4）3142353lim22xxxxx原式=22433531xxxx=31（5）535sinsin3lim0xxx原式=xxxxx55sin33sin5lim30=53（6）42)sin(4lim22xxx原式=22)sin(2lim2xxxx=22)sin(lim2)(lim22xxxxx=42．设函数0sin0,0,1sin)(xxxxaxbxxxf，问：（1）当a,b为何值时，f(x)在x0处有极限存在？（2）当a,b为何值时，f(x)在x0处连续.解：(1)1()lim,()lim00fxbxfxx当1f(0)limf(x)1x0时，有ba(2).1f(0)limf(x)1bax0有时，当函数f(x)在x=0处连续.3．计算下列函数的导数或微分：（1）2222log2xxyx，求y答案：ln212ln22xxyx（2）dcxbaxy，求y答案：22)()()()(dcxbcaddcxbcaxdacxy（3）531xy，求y答案：235)2(33xy（4）xxxye，求y答案：)(21xxxeexy=xxxeex21（5）bxyeaxsin，求yd答案： )cos(sincossin)(sin)(sin(bxbbxebxbebxaebxebxeyaxaxaxaxax∴bxdxbbxaedyax)cos(sin（6）xxyx1e，求yd答案： xxeyx23112∴dxxexdyx)123(12（7）e2cosxxy，求yd答案： )()(sin22xexxyx=222sinxxexx∴dxxexxdyx)22sin(2（8）nxxynsinsin，求y答案：nxnxxnyncoscossin1（9）)1ln(x2xy，求y答案：)1(1122xxxxy=)11(1122xxxx=2221111xxxxx=211x（10）xxxyx21232cot1，求y答案：531cos261211cos6121ln2sin1212)(ln2(cos1)2xxxxxxxyxxy是x的隐函数，试求y或yd(1)方程两边对x求导：0322xyyyyx32)(2xyxyy所以dxxyxydy232(2)方程两边对x求导：4)())(1cos(xyyeyyxxyxyxyyeyxyxeyx)cos(4])[cos(所以xyxyxeyxyeyxy)cos()cos(45．求下列函数的二阶导数：（1）)1ln(x2y，求y答案：(1)212xxy222222)1(22)1(22)1(2xxxxxxy(2)212321212121)(xxxxy23254143xxy14143)1(y作业（二）（一）填空题cxxxfx22)d(，则___________________()xf.答案：22ln2x2.xxd(sin)________.答案：xcsin3.若cFxxfx())d(，则xxxf)d1(2.答案：cxF)1(212___________)dln(1dde12xxx.答案：05.若ttxPxd11)(02，则__________()Px.答案：211x（二）单项选择题1.下列函数中，（D）是xsinx2的原函数．A．21cosx2B．2cosx2C．-2cosx2D．-21cosx22.下列等式成立的是（C）．A．d(cos)sindxxxB．d(1)lndxxxC．l...