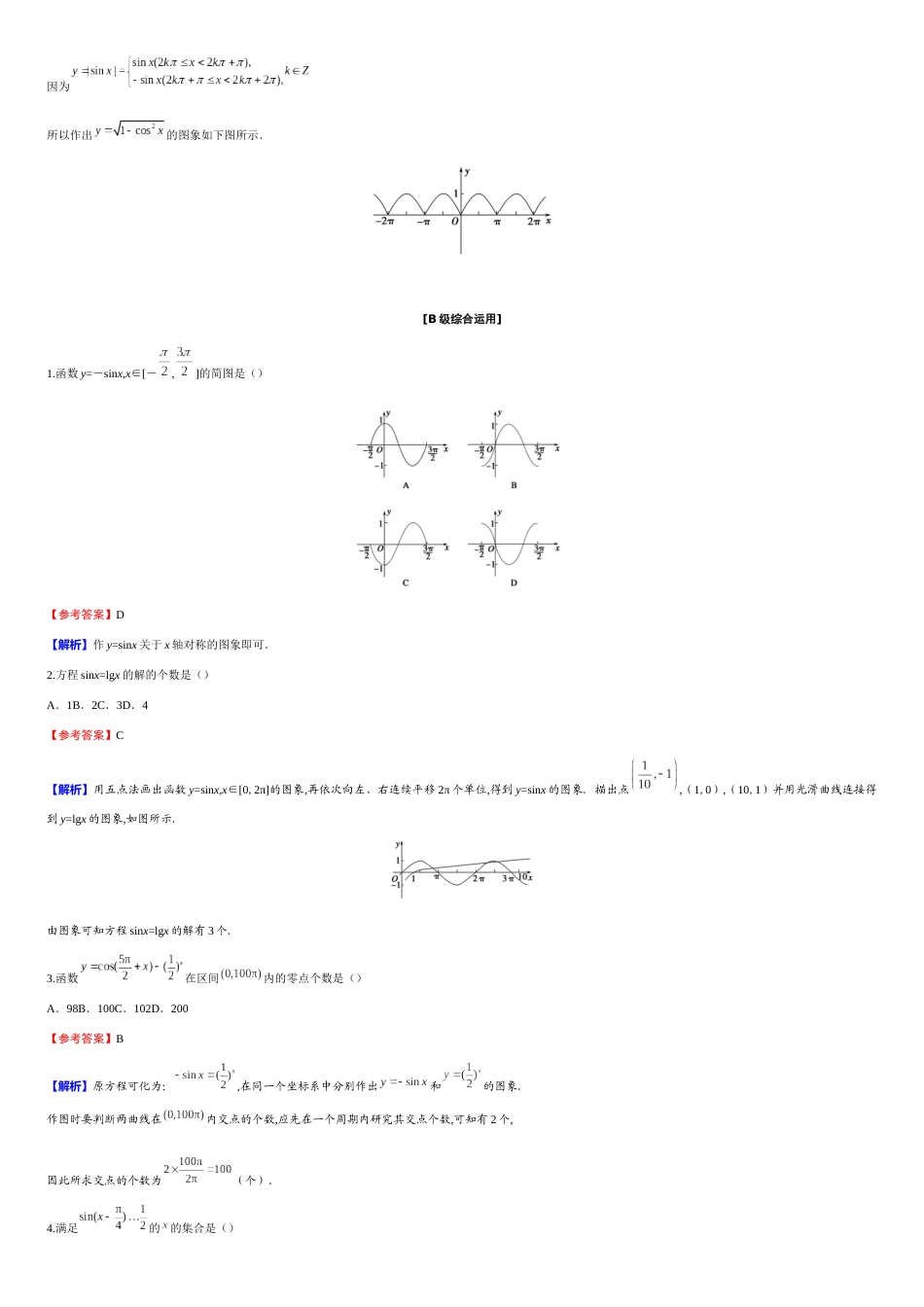
备作业5.4.1正余弦函数图象[A级基础稳固]1.函数的大致图象是图中的（）【参考答案】B【解析】根据“五点法”确定其图象．2．函数与函数的图象关于（）A．轴对称B．轴对称C．原点对称D．直线对称【参考答案】A【解析】在同一坐标系中画出函数与函数的图象,可知它们关于轴对称．3.方程的实根个数是（）A．1B．2C．3D．无数个【参考答案】D【解析】作出和的图象,可知它们有无数个交点．4.在上,满足的的取值范围是（）A．B．C．D．【参考答案】B【解析】根据的图象可知：当时,或,∴,得．5．【原创题】先将y=sinx－1的图象向左平移个单位长度,再向上平行移动1个单位长度,得到函数f（x）的图象,则f（x）=________．【参考答案】cosx【解析】由y=sin－1＋1知y=cosx,即f（x）=cosx．6.下列函数中：①y=sinx－1；②y=|sinx|；③y=－cosx；④y=；⑤y=；与函数y=sinx形状完全相同的有________．【参考答案】①③【解析】①y=sinx－1是将y=sinx向下平移1个单位,没改变形状；③y=－cosx=sin（x－）是由y=sinx向右平移个单位而得到,没改变形状,与y=sinx形状相同；∴①③与y=sinx的形状完全相同；而②y=|sinx|,④y==|cosx|和⑤y==|sinx|与y=sinx的形状不相同．7.【改编题】的图象与的交点的个数是．【参考答案】2【解析】由的图象向上平移1个单位,得的图象,故在上与交点的个数是2个．8.已知点在余弦曲线上,则（）A．B．C．D．【参考答案】B【解析】．9．函数y=cosx（x∈R）的图象向右平移个单位后,得到函数y=g（x）的图象,则g（x）的解析式为（）A．－sinxB．sinxC．－cosxD．cosx【参考答案】B【解析】10．函数的简图是（）【参考答案】D【解析】把的图象向上平移1个单位即可．11.【原创题】方程的正实根个数是（）A．0B．1C．2D．无数个【参考答案】A【解析】由与的图象可知两图象在第一、四象限及轴的正半轴上无交点．12.【改编题】若函数的图象和直线围成一个封闭的平面图形,则这个封闭图形的面积是（）A．4B．8C．2D．4【参考答案】D【解析】作出函数,的图象,函数,的图象与直线围成的平面图形是如图所示的阴影部分．利用图象的对称性可知该平面图形的面积等于矩形的面积,又 ,,∴．13．若x∈[－π,π）,则满足cosx≥的x的取值范围是________．【参考答案】【解析】如图知x∈．14.方程x2－cosx=0的实数解的个数是________．【参考答案】2【解析】作函数y=cosx与y=x2的图象,如图所示,由图象,可知原方程有两个实数解．15.【改编题】如果,则函数的定义域为．【参考答案】【解析】依题意得即∴．16.作出函数的图象．【解析】将化为,因为所以作出的图象如下图所示．[B级综合运用]1.函数y=－sinx,x∈[－,]的简图是（）【参考答案】D【解析】作y=sinx关于x轴对称的图象即可．2.方程sinx=lgx的解的个数是（）A．1B．2C．3D．4【参考答案】C【解析】用五点法画出函数y=sinx,x∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y=sinx的图象．描出点,（1,0）,（10,1）并用光滑曲线连接得到y=lgx的图象,如图所示．由图象可知方程sinx=lgx的解有3个．3.函数在区间内的零点个数是（）A．98B．100C．102D．200【参考答案】B【解析】原方程可化为：,在同一个坐标系中分别作出和的图象．作图时要判断两曲线在内交点的个数,应先在一个周期内研究其交点个数,可知有2个,因此所求交点的个数为（个）．4.满足的的集合是（）A．B．C．D．【参考答案】A【解析】利用正弦函数图象,当时,,即．5．【改编题】函数,的图象在区间的交点个数为（）A．B．C．D．【参考答案】B【解析】令,即,得,则该方程在区间上的实根为、、、,共个.故选：B.6．函数的图象是（）【参考答案】C【解析】6．从图象上可以看出：若与的图象有且仅有两个交点,则的范围为．7.【改编题】已知函数与,它们的图象有一个横坐标为的交点,则的值是______.【参考答案】【解析】因为函数与有一个交点的横坐标为则即由正弦函数的图像与性质可知或因为所以当时,代入可求得故参考答案为:8.【原创题】函数,则不等式f(x)>的解集是__．【参考答案】【解析】当x＜0时,不等式f（x）>可化为x+2＞,解得x＞﹣,结合x＜0可得﹣＜x＜0；当x≥0时,不等式f（x）>可化为sinx...