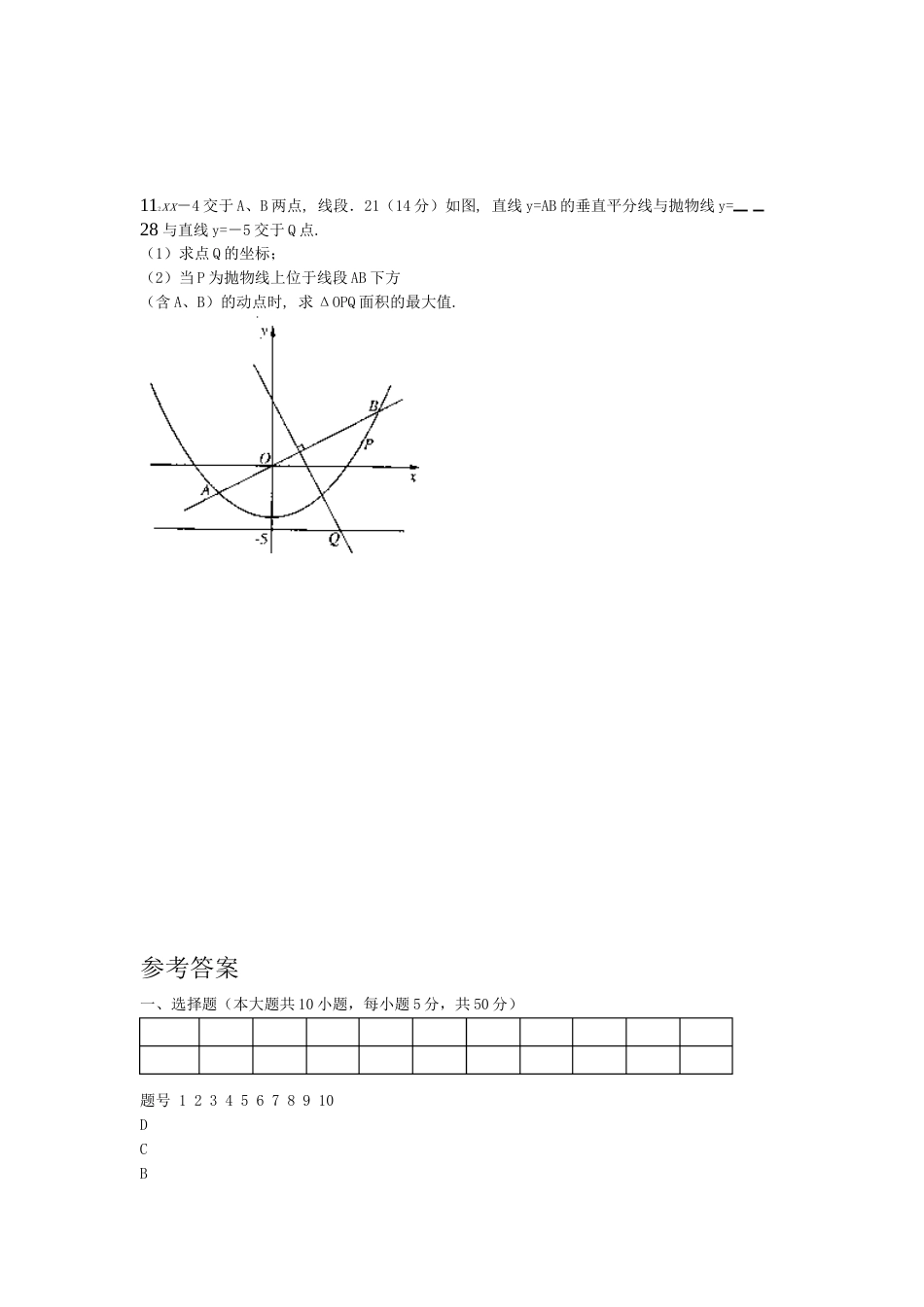
抛物线测试题小题，每小题5分，共50分）一、选择题（本大题共102x2y?1．抛物线（）的焦点坐标是111．A．B．C．D)0,(),0(1),(0),(0844，则抛物轴上，其上的点到焦点的距离为52．已知抛物线的顶点在原点，焦点在y)P(m,?3（）线方程为D．A．B．C．2222yx4??y?8xyx8??yx4?23．抛物线）截直线所得弦长等于（x12?y1?2x?y1515．．B．CD．A151522）2,3)，则它的方程是（4．顶点在原点，坐标轴为对称轴的抛物线过点(－4499492222或D.或A.C.B.xy?y?x2y?x?2x?y?y?xx?y?3322322?tx?)0(1,P）（到曲线5．点（其中参数）上的点的最短距离为R?t?ty?2?2D．．．1CA．0B22若，的焦点有三点，是物6．抛线它上)0(py??2pxF)x(,y(x,y),CxA(,y),B312213CF,AF,BF成等差数列，则）（成等差数列B．A．成等差数列x,x,x,x,xx232131成等差数列D．C．成等差数列y,y,y,yy,y232311P2是抛物线上的一动点，则的焦点，点2），为抛物线7．若点A的坐标为（3，x?y2FPBPA?P）的坐标是（取得最小值时点1．）DC．（2，2（A．（0，0）B．1，1）)(,122)0?px(py?2)y(x,(x,y),BAAB则关系式8．已知抛物线的两端点为,的焦点弦2112yy的值一定等于（）21xx212D．－p．4C．pB．－4A2y?ax(a?0)的焦点F作一直线交抛物线于P，Q两点，若线段PF与9．过抛物线FQ的长11?qp,=（分别是），则qp41．．B．DCA．aa42aa22xaa>2p)，则AB的中点M到为抛物线y=2py(p>0)的动弦，且|AB|=(轴的最近AB10．若距离是（）aa?pa?pp．．AB．CD．2222二、填空题（本大题共5小题，每小题5分，共25分）2上到其准线和顶点距离相等的点的坐标为．______________11、抛物线xy?2x?8y01?x?y?12、直线截抛物线，所截得的弦中点的坐标是2)?2px(p?0y则此抛物线焦点与准，的点到焦点的距离为5上，横坐标为4、13抛物线线的距离为2x4y?0FA?FB?FC?CA，B，F为抛物线14的焦点，、设为该抛物线上三点，若，?FC?FB?FA则15、对于顶点在原点的抛物线，给出下列条件；轴上；2（）焦点在x（1）焦点在y轴上；；4）抛物线的通径的长为5（3）抛物线上横坐标为1的点到焦点的距离等于6；（1）．（5）由原点向过焦点的某条直线作垂线，垂足坐标为（2，2x______．其中适合抛物线y=10的条件是(要求填写合适条件的序号）三、解答题2px?2yxx的重上，△ABC，（28），B（，y），C（，y）在抛物线分）已知点16．（12A2211F重合（如图）心与此抛物线的焦点的坐标；1）写出该抛物线的方程和焦点F（中点M的坐标；）求线段（2BC.BC所在直线的方程）求（321ax?y?a0x?y?的取上恒有关于直线分）已知抛物线对称的相异两点，求12．17（.值范围2x、两点，再以、交抛物线作直线，－，过点的焦点为12．18（分）抛物线=4yF(01)LABAF.，试求动点为邻边作平行四边形BFFARBR的轨迹方程2)?0p?2px(yCC：分）已知抛物线的方程19、（1，-2）.（12过点AC的方程，并求其准线方程；（I）求抛物线ClOOAl有公共点，II）是否存在平行于，使得直线（为坐标原点）的直线与抛物线（5lOAl5的方程；若不存在，说明理由与的距离等于.？若存在，求出直线且直线2=4ax(0＜a＜1＝的焦点为F，以A(a+4,0)y．20（13分）已知抛物线为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点．（1）求｜MF｜+｜NF｜的值；aa的如存在，求出｜成等差数列｜、｜｜、｜）是否存在这样的（2值，使｜MFPFNF?.值，若不存在，说明理由．112xx－4交于A、B两点,线段．21（14分）如图,直线y=AB的垂直平分线与抛物线y=28与直线y=－5交于Q点.（1）求点Q的坐标；（2）当P为抛物线上位于线段AB下方（含A、B）的动点时,求ΔOPQ面积的最大值.参考答案一、选择题（本大题共10小题，每小题5分，共50分）题号12345678910DCBCABBADC答案．24分）二、填空题（本大题共4小题，每小题6分，共21）2（13．15．．，（5）12．11)(,?48分）题，共76三、解答题（本大题共6222?8?2py?2px，8）在抛物线上，有15．（12分）[解析]：（1）由点A（2，2xy?32.所以抛物线方程为8，0），焦点F的坐标为（解得p=16.的是线段AMM0）是△ABC的重心，是BC的中点，所以F（2）如图，由于F（8，AF)yx,(的坐标为，则定比分点，且，设点M2?00FMy28?2?2x，，解得4?x?11,y?000,?...