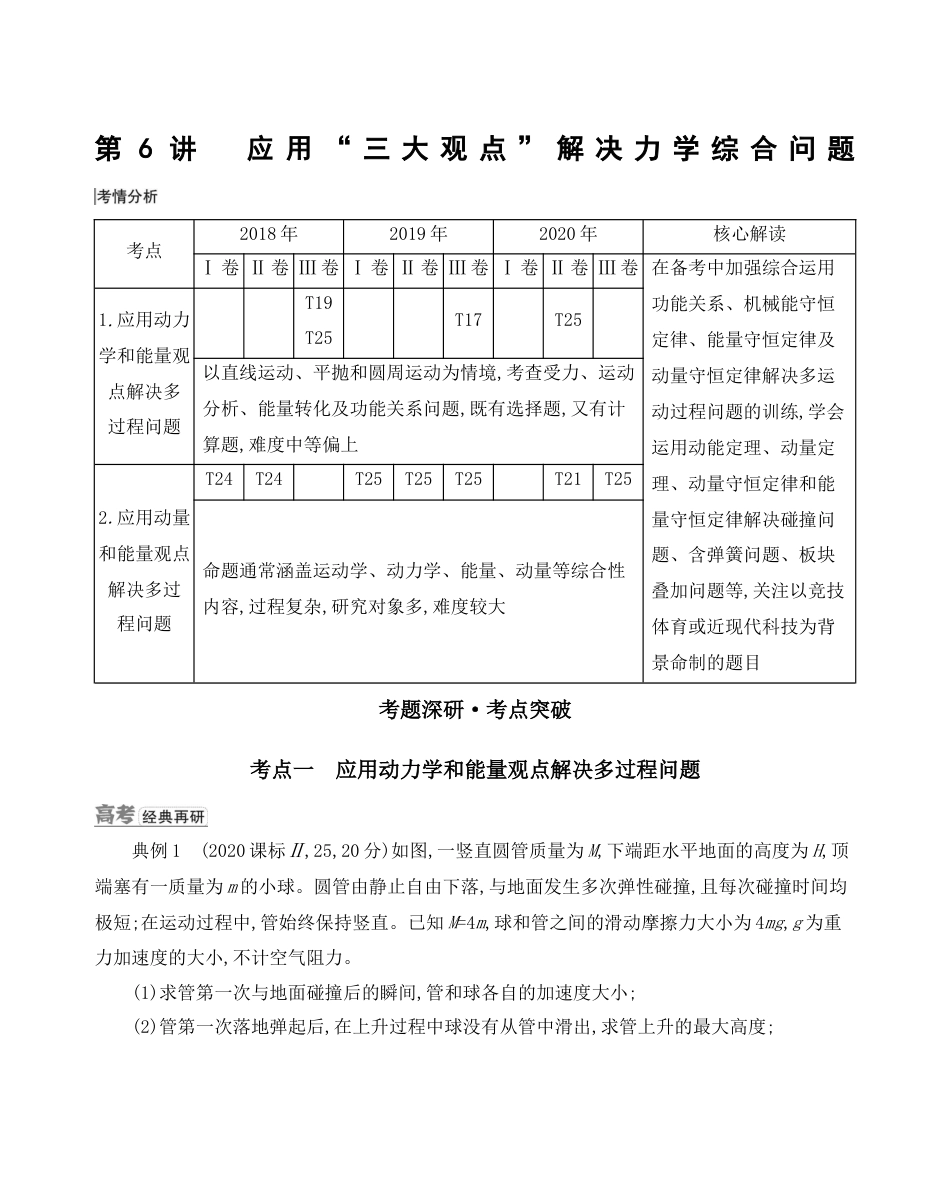
第6讲应用“三大观点”解决力学综合问题考点2018年2019年2020年核心解读Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷Ⅰ卷Ⅱ卷Ⅲ卷在备考中加强综合运用功能关系、机械能守恒定律、能量守恒定律及动量守恒定律解决多运动过程问题的训练,学会运用动能定理、动量定理、动量守恒定律和能量守恒定律解决碰撞问题、含弹簧问题、板块叠加问题等,关注以竞技体育或近现代科技为背景命制的题目1.应用动力学和能量观点解决多过程问题T19T25T17T25以直线运动、平抛和圆周运动为情境,考查受力、运动分析、能量转化及功能关系问题,既有选择题,又有计算题,难度中等偏上2.应用动量和能量观点解决多过程问题T24T24T25T25T25T21T25命题通常涵盖运动学、动力学、能量、动量等综合性内容,过程复杂,研究对象多,难度较大考题深研·考点突破考点一应用动力学和能量观点解决多过程问题典例1(2020课标Ⅱ,25,20分)如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M=4m,球和管之间的滑动摩擦力大小为4mg,g为重力加速度的大小,不计空气阻力。(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。本题通过圆管和小球在竖直方向上的作用与圆管和地面的碰撞过程,考查了牛顿第二定律及运动学公式、动能定理等相关规律,考查了考生综合分析能力及应用数学知识处理物理问题的能力,体现了模型建构、科学推理等核心素养要素。思维拆解规范答题过程一:圆管由静止自由下落,第一次与地面碰撞后的瞬间,圆管速度变成竖直向上,小球仍然向下运动,此时球与管之间的摩擦力是什么方向?能否根据牛顿第二定律求出它们的加速度?答案(1)2g3g(2)1325H(3)见解析解析(1)管第一次落地弹起的瞬间,小球仍然向下运动。设此时管的加速度大小为a1,方向向下;球的加速度大小为a2,方向向上;球与管之间的摩擦力大小为f,由牛顿运动定律有Ma1=Mg+f①ma2=f-mg②联立①②式并代入题给数据,得a1=2g,a2=3g③(2)管第一次碰地前与球的速度大小相同。由运动学公式,碰地前瞬间它们的速度大小均为v0=❑√2gH④方向均向下。管弹起的瞬间,管的速度反向,球的速度方向依然向下。设自弹起时经过时间t1,管与小球的速度刚好相同。取向上为正方向,由运动学公式v0-a1t1=-v0+a2t1⑤过程二:球与管在与地面碰撞之前一直做自由落体运动,根据运动学基本公式可以求出球与管第一次碰地时速度,由于每次落地后向上弹起瞬间的速度与落地时速度大小相等,可得到管碰地后管的速度与球的速度大小相等,方向相反,管碰地后向上做匀减速运动,球向下做匀减速运动,球和管的速度哪个先减小到零?联立③④⑤式得t1=25❑√2Hg⑥设此时管下端的高度为h1,速度为v。由运动学公式可得h1=v0t1-12a1t12⑦v=v0-a1t1⑧由③④⑥⑧式可判断此时v>0。此后,管与小球将以加速度g减速上升h2,到达最高点。由运动学公式有h2=v22g⑨设管第一次落地弹起后上升的最大高度为H1,则H1=h1+h2联立③④⑥⑦⑧⑨⑩式可得H1=1325H(3)设第一次弹起过程中球相对管的位移为x1。在管开始下落到上升H1这一过程中,由动能定理有Mg(H-H1)+mg(H-H1+x1)-4mgx1=0联立式并代入题给数据得x1=45H同理可推得,管与球从再次下落到第二次弹起至最高点的过程中,球与管的相对位移x2为x2=45H1设圆管长度为L。管第二次落地弹起后的上升过程中,球不会滑出管外的条件是x1+x2≤L过程三:当球的速度先减小到零时,管还具有向上的速度,此时球受到管的摩擦力变了吗?球的加速度变了吗?球的速度方向开始向哪?过程四:当球反向向上加速达到与管共速时,球和管间的摩擦力会怎样突变?能否根据运动学公式求得自管第一次与地面碰撞瞬间到第一次达到共速所用的时间和共同速度的大小?球与管共速后将做什么运动?过程五:管第二次落地弹起的过程与第一次的过程类似,用同样的方法可得到管第二次落地弹起后球与管的相对位移,要满足管第二次弹起后球不致滑落,即要第一次落地弹起后球与管的相对位移与管第...