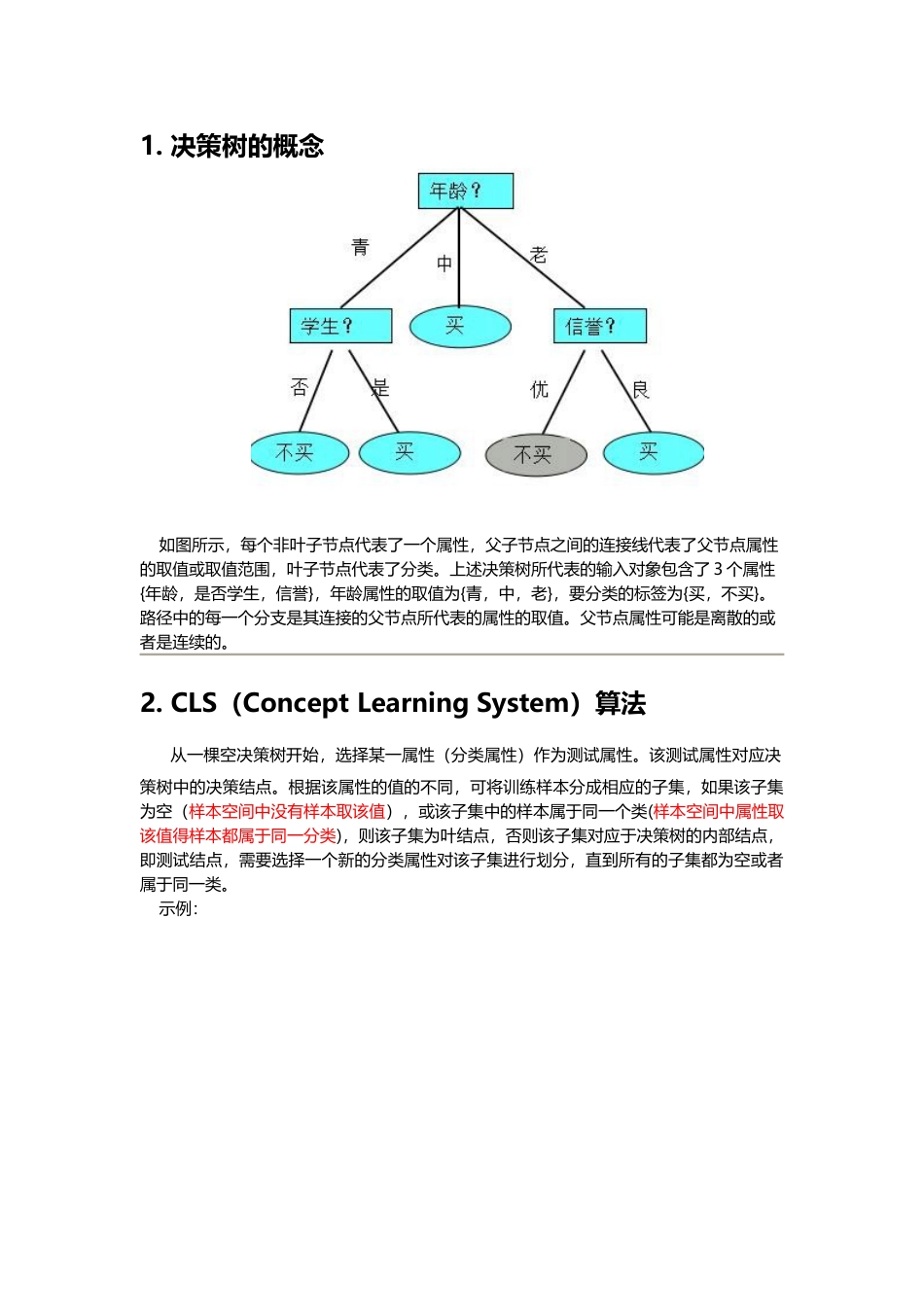
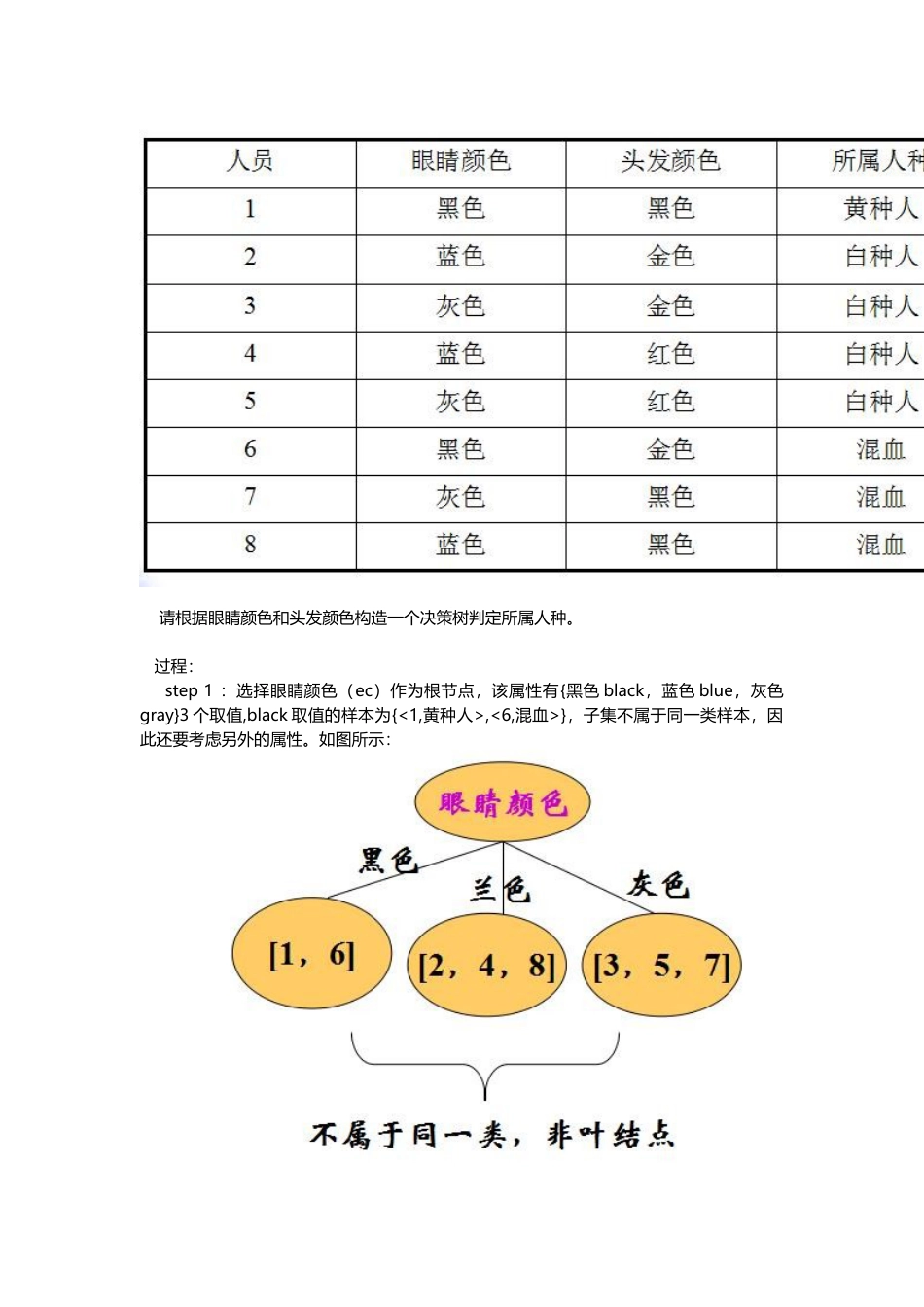
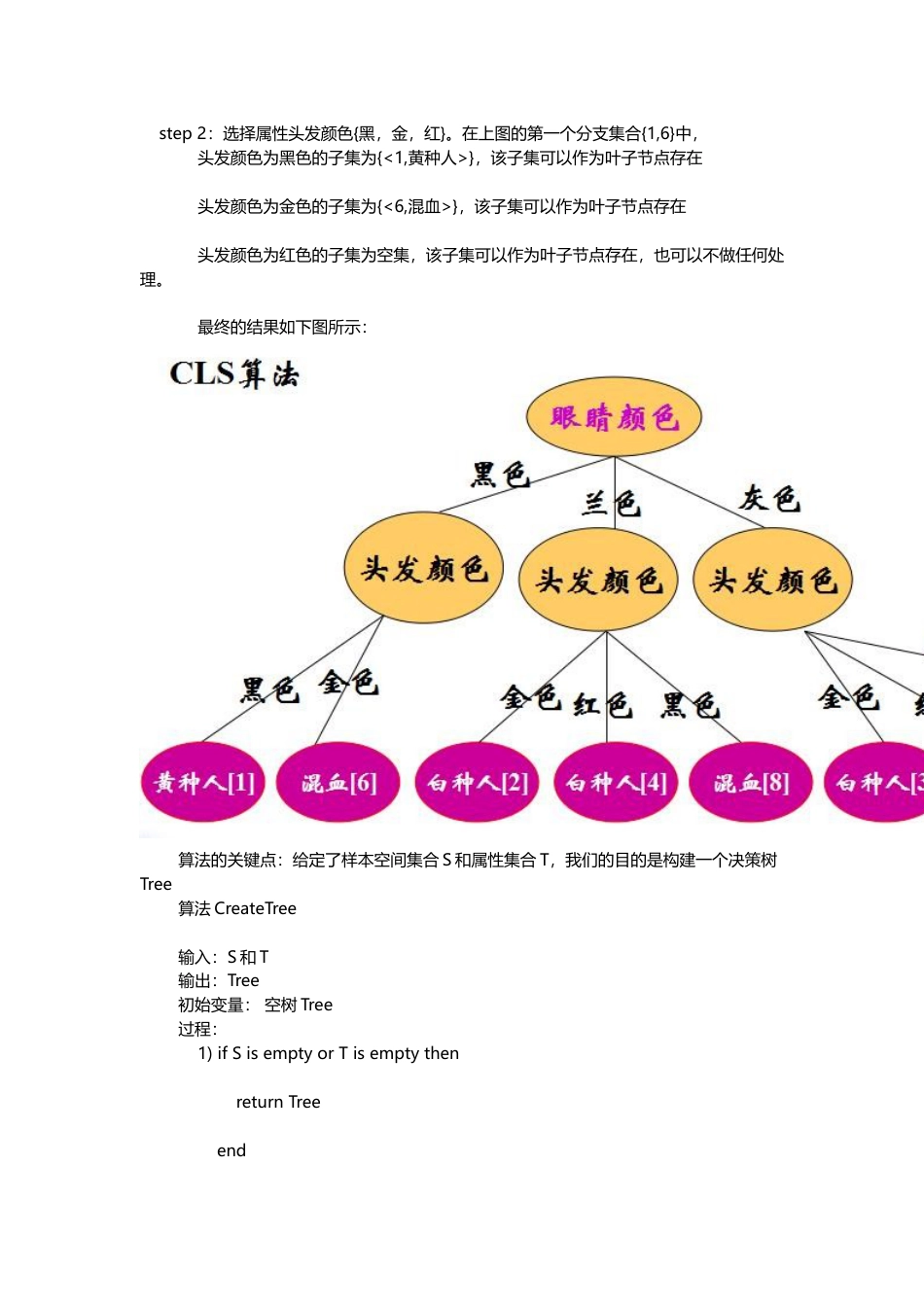
1.决策树的概念如图所示,每个非叶子节点代表了一个属性,父子节点之间的连接线代表了父节点属性的取值或取值范围,叶子节点代表了分类。上述决策树所代表的输入对象包含了3个属性{年龄,是否学生,信誉},年龄属性的取值为{青,中,老},要分类的标签为{买,不买}。路径中的每一个分支是其连接的父节点所代表的属性的取值。父节点属性可能是离散的或者是连续的。2.CLS(ConceptLearningSystem)算法从一棵空决策树开始,选择某一属性(分类属性)作为测试属性。该测试属性对应决策树中的决策结点。根据该属性的值的不同,可将训练样本分成相应的子集,如果该子集为空(样本空间中没有样本取该值),或该子集中的样本属于同一个类(样本空间中属性取该值得样本都属于同一分类),则该子集为叶结点,否则该子集对应于决策树的内部结点,即测试结点,需要选择一个新的分类属性对该子集进行划分,直到所有的子集都为空或者属于同一类。示例:请根据眼睛颜色和头发颜色构造一个决策树判定所属人种。过程:step1:选择眼睛颜色(ec)作为根节点,该属性有{黑色black,蓝色blue,灰色gray}3个取值,black取值的样本为{<1,黄种人>,<6,混血>},子集不属于同一类样本,因此还要考虑另外的属性。如图所示:step2:选择属性头发颜色{黑,金,红}。在上图的第一个分支集合{1,6}中,头发颜色为黑色的子集为{<1,黄种人>},该子集可以作为叶子节点存在头发颜色为金色的子集为{<6,混血>},该子集可以作为叶子节点存在头发颜色为红色的子集为空集,该子集可以作为叶子节点存在,也可以不做任何处理。最终的结果如下图所示:算法的关键点:给定了样本空间集合S和属性集合T,我们的目的是构建一个决策树Tree算法CreateTree输入:S和T输出:Tree初始变量:空树Tree过程:1)ifSisemptyorTisemptythenreturnTreeend2)selecttfromTandcreateatreenodeparentNodeastheroot3)splitSinS1,S2,...,Skbythevalueoft(根据t的k个可能取值,将S划分为子集S1,S2,...Sk)4)foreachSidoifthesamplesinsihavesameclasslabeltheninserttheclasslableasthechildnodeforparentNodeelsechildTree=CreateTree(Si,T-t)addchildTreerootasthechildNodeforparentNodeendend5)T<-T-tandgoto1)算法的注意点:在步骤2中selecttfromT表示从T中抽取出一个属性,抽取哪个属性是算法的关键;在步骤4的循环中,CreateTree(si,T.Copy()),使用的是T的一个拷贝,这样保证了对于S的每一个子集Si,使用的是相同的属性集合。3.ID3算法该方法使用信息增益度选择测试属性。小概率事件比大概率事件包含的信息量大。如果某件事情是“百年一见”则肯定比“习以为常”的事件包含的信息量大。事件ai的信息量I(ai)可如下度量:其中p(ai)表示事件ai发生的概率。假设有n个互不相容的事件a1,a2,a3,….,an,它们中有且仅有一个发生,则其平均的信息量可如下度量:当p(ai)=0或者p(ai)=1的时,信息量I(ai)=0,也就是不可能事件和必然事件的信息量为0.信息熵的定义:一个变量X,它可能的取值有n多种,分别是x1,x2,……,xn,每一种取到的概率分别是P1,P2,……,Pn,那么X的熵就定义为:意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大。对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。结论:ID3–信息量大小的度量Gain(S,A)是属性A在集合S上的信息增益Gain(S,A)=Entropy(S)-Entropy(S,A)Entropy(S,A)=∑(|Sv|/|S|)*Entropy(Sv)∑是属性A的所有可能的值v,Sv是属性A有v值的S子集|Sv|是Sv中元素的个数;|S|是S中元素的个数。用P(Ci,Sv)表示Sv中包含有属于分类Ci的样本概率,I(Ci,Sv)表示子集合Sv中属于分类Ci的样本信息,则熵Entropy(Sv)=∑I(Ci,Sv),求和发生在C=c1,c2,...,Ck上。示例:...