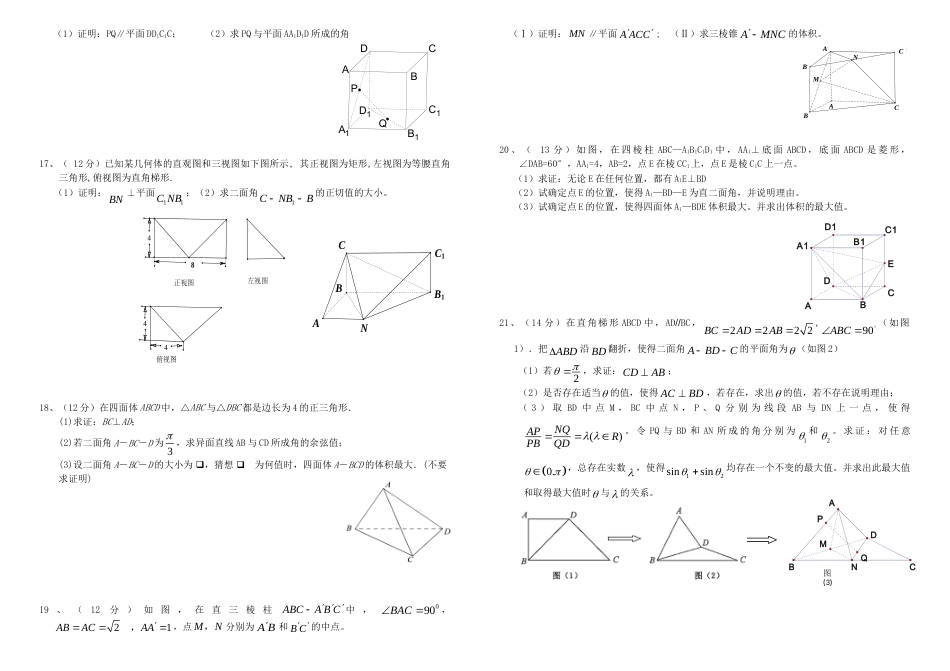
ABCDA1B1C1D1高2012级第三期10月阶段性考试数学试题(理科)一、选择题(每题5分,共50分)1、右图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是()2、设a,b,c是空间三条直线,,是空间两个平面,则下列命题不成立的是()A.当c时,若c⊥,则∥B.当b,且c是a在内的射影时,若b⊥c,则a⊥bC.当b时,若b⊥,则D.当b,且c时,若c∥,则b∥c3、如图,ABCD-A1B1C1D1为正方体,下面结论错误的是().A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD与CB1角为60°4、已知△ABC的斜二侧直观图是边长为2的等边△A1B1C1,那么原△ABC的面积为()A.2B.C.2D.5、棱长为1的正方体ABCD-A1B1C1D1中,四面体AB1CD1的体积为()A.41B.31C.21D.326、下列命题中正确的是()A.若平面M外的两条直线在平面M内的射影为一条直线及此直线外的一个点,则这两条直线互为异面直线B.若平面M外的两条直线在平面M内的射影为两条平行直线,则这两条直线相交C.若平面M外的两条直线在平面M内的射影为两条平行直线,则这两条直线平行D.若平面M外的两条直线在平面M内的射影为两条互相垂直的直线,则这两条直线垂直7、在空间四边形ABCD中,,,,EFGH分别是,,,ABBCCDDA的中点。若ACBDa,若四边形EFGH的面积为238a,则异面直线AC与BD所成的角为()A、030B、060;C、0120;D、060或0120。8、若直角三角形的斜边与平面平行,两条直角边所在直线与平面所成的角分别为21和,则()A.1sinsin2212B.1sinsin2212C.1sinsin2212D.1sinsin22129、一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为1h、2h、h,则1:2:hhh()A.3:1:1B.3:2:2C.3:2:2D.3:2:310、如图,在2,,,ABCABACADBCABBDBC中若则;类似地有命题:在三棱锥A—BCD中,AD面ABC,若A点在BCD内的射影为M,则有BCDBCMABCSSS2。上述命题是()A.真命题B.增加条件“ABAC”才是真命题C.增加条件“BCDM为的垂心”才是真命题D.增加条件“三棱锥A—BCD是正三棱锥”才是真命题二、填空题(每题5分,共25分)11、已知A(3,5,-7)和点B(-2,4,3),点A在x轴上的射影为A′,点B在z轴上的射影为B′,则线段A′B′的长为_______.12、一空间几何体的三视图如图所示,则该几何体的体积为。PABQCDC1D1B1A1CDABGM(12题图)(13题图)(14题图)13、如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于。14、已知正方体的棱长ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,M为面ABCD上一点,则1DMGM的最小值为。15、已知三棱柱111ABCABC的侧棱与底面边长都相等,有以下命题①若1A在底面ABC内的投影为△ABC的中心,则0160AAB;②若1A在底面ABC内的投影为△ABC的中心,则1AB与面ABC所成角的正弦值为33;③若1A在底面ABC内的投影为线段BC的中点,则二面角1AABC的正切值为233④若1A在底面ABC内的投影为线段BC的中点,则1AB与面ABC所成角的正弦值为1414三、解答题(共75分)16、(12分)正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心。(第3题)O1C1B1AxyC1D1B1A1CDABE(1)证明:PQ∥平面DD1C1C;(2)求PQ与平面AA1D1D所成的角B1A1D1C1BADCPQ17、(12分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(1)证明:BN⊥平面11CNB;(2)求二面角1CNBB的正切值的大小。俯视图44左视图正视图8C1B14CANB18、(12分)在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.(1)求证:BC⊥AD;(2)若二面角A-BC-D为3,求异面直线AB与CD所成角的余弦值;(3)设二面角A-BC-D的大小为,猜想为何值时,四面体A-BCD的体积最大.(不要求证明)19、(12分)如图,在直三棱柱ABCABC中,900BAC,21ABACAA,...