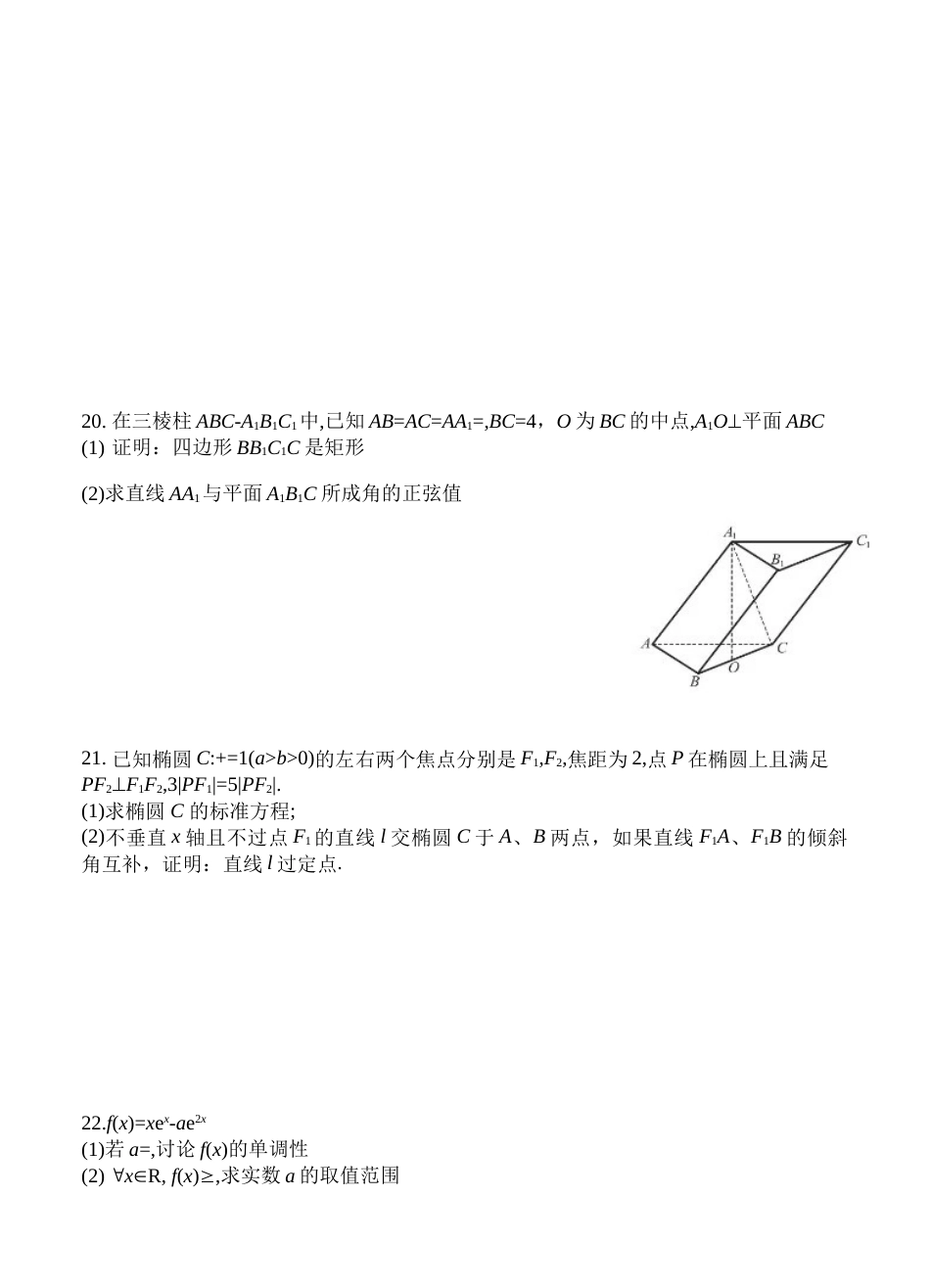
2020-2021学年莆田一中高三数学期中考试卷命题人:审核人:高三备课组(满分:150分,时间:120分钟)一、选择题(8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题意)1.设集合A={y|y=},B={x|y=},则()A．A=BB.AB=C.ABD.BA2.复数z满足iz=1-2i,是z的共轭复数则z=()A.B.C.3D.53.已知向量a=(1,1),b=(-1,3),c=(2,1)且(a-b)c,则=()A.3B.2C.-2D.-34.已知f(x)=e-x+kex(k为常数),那么函数f(x)的图象不可能是()ABCD5.在平面直角坐标系xOy中,角与角均以Ox为始边,它们的终边关于y轴对称.若sin=,则cos(-)=()A.B.C.-D.-6.把物体放在冷空气中冷却,如果物体原来的温度为1C,空气温度为0C,那么t分钟后物体的温度(单位C)可由公式：=0+(1-0)e-kt求得,其中k是一个随着物体与空气的接触状况而定的正常数.现有100C的物体,放在20C的空气中冷却,4分钟后物体的温度是60C，则再经过m分钟后物体的温度变为40C(假设空气温度保持不变),则m=()A.2B.4C.6D.87.已知P是椭圆C:+=1(a>b>0)上的点,F1,F2分别是C的左,右焦点，O是坐标原点,若|OP+OF2|=2|OF1|且F1PF2=60，则椭圆的离心率为()A.B.C.D.8.集合论中著名的“康托三分集”是数学理性思维的产物,具有典型的分形特征,其具体操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段(,),记为第一次操作;再将剩余的两个区间[0,],[,1]分别均分为三段,并各自去掉中间的区间段,记为第二次操作；；如此这样,每次在上一次操作的基础上将剩下的各个区间分别均分为三段，同样各自去掉中间的区间段，操作的过程不断进行下去，以至无穷，剩下的区间集合即是“康托三分集”。若使去掉的各区间长度之和不小于,则需要操作的次数n的最小值为()参考数据:lg20.301,lg30.4771A.4B.5C.6D.7二、选择题(4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分)9.已知等差数列{an}的前n项和为Sn,a2=18,a5=12,则下列选项正确的是()A.d=-2B.a1=22C.a3+a4=30D.当且仅当n=11时,Sn取得最大值10.已知A(-2,0),B(2,0),若圆(x-2a+1)2+(y-2a-2)2=1上存在点M满足MAMB=0,实数a可以是()A.-1B.-0.5C.0D.111.若2x=3,3y=4,则下列选项正确的有()A.y<B.x>yC.+y>2D.x+y>212.设函数f(x)=ax-xa(a>1)的定义域为(0,+),已知f(x)有且只有一个零点,下列结论正确的有()A.a=eB.f(x)在区间(1,e)单调递增C.x=1是f(x)的极大值点D.f(e)是f(x)的最小值三、填空题(本题共4小题,每小题5分,共20分)13.函数f(x)=ex+sinx在点(0,1)处的切线方程为.14.将函数y=f(x)图象右移个单位,再把所得的图象保持纵坐标不变,横坐标伸长到原来的2倍得到y=sin(x-),则f()=_______15.在长方体ABCD-A1B1C1D1中,AB=CC1=,BC=1,点M为正方形CDD1C1对角线的交点,则三棱锥M-A1CC1的外接球表面积为_________16.某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,O1为圆孔及轮廓圆弧AB所在圆的圆心,O2为圆弧CD所在圆的圆心,点A是圆弧AB与直线AC的切点,点B是圆弧AB与直线BD的切点,点C是圆弧CD与直线AC的切点,点D是圆弧CD与直线BD的切点，O1O2=18cm,AO1=6cm,CO2=15cm,圆孔O1的半径为3cm,则图中阴影部分的的面积为________cm2四、解答题(本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤)17.在①sinA=2sinB，②a+b=6，③ab=12.这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在求出ABC的面积；若问题中的三角形不存在，说明理由.问题:是否存在ABC,它的内角ABC的对边分别为a，b，c且asin=csinA,c=3,______18.已知Sn是数列{an}的前n项和,Sn+1=3Sn+1,a1=1(1)证明:数列{an}是等比数列，并求an的通项公式(2)若bn=(-1)n-1nan,求数列{bn}的前n项和Tn19.在ABC中,A=,D为线段BC边上一点，BD=3,BAD=(1)若AB=3,求AD(2)若CD=4,求tanBABCD20.在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=,BC=4，O为BC的中点,A1O平面ABC(1)证明：四边形BB1C1C是矩形(2)求直线AA1与平面A1B1C所成角的正弦值21.已知椭圆C:+=1(a>b>0)的左右两个焦点分别是F1,F2,焦距为2,点P在椭圆上且满足PF2F1F2,3|PF1|=...