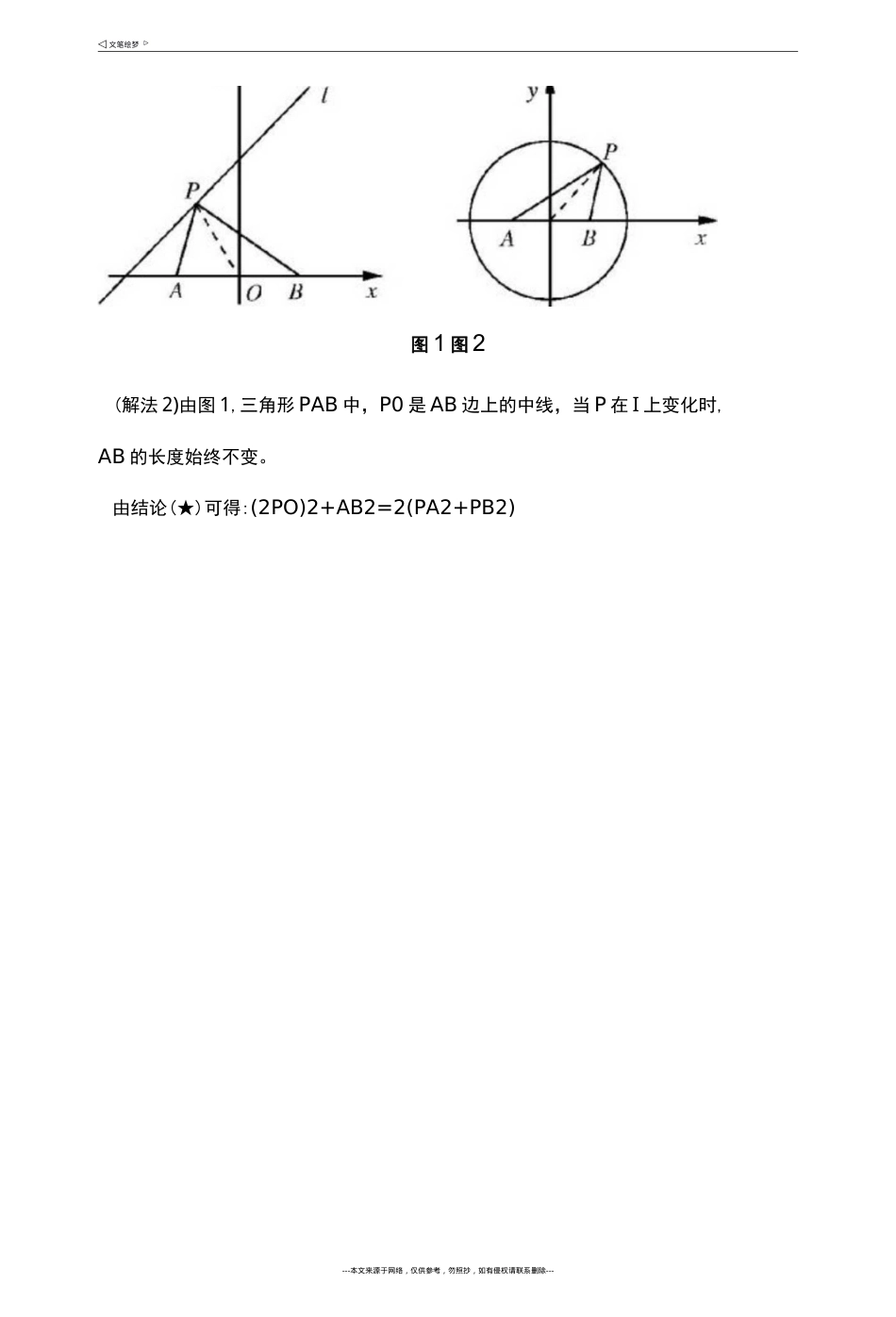
浅谈探究性学习模式在数学教学中运用•中学数学论文浅谈探究性学习模式在数学教学中运用郝凯(宿豫中学，江苏宿迁223800)摘要：探究性教学模式指的是在教学过程中,学生在教师指导下,通过以〃自主、探究、合作"为特征的学习方式对当前教学内容中的主要知识点进行自主学习、深入探究并进行小组合作交流，从而较好地达到课程标准中关于认知目标与情感目标要求的一种教学模式。关键词:探究性学习；学习模式；数学教学:G633文献标识码：A:1005-6351(2013)-01-0149-01在探究性学习实施过程中强调学生的主体作甩同时也重视教师的指导作用。在课堂中，教师要有效,有步骤地指导学生开展活动。在课堂上,探究的问题一旦确立，学生可自由地组成3〜5人的合作探究小组。在探究活动开始前，应指导学生做好各项准备工作。其探究方案是否切实可行，能否保证有严密的科学性，教师必须加以指导。在探究性活动中，要引导学生一方面将所学的理论知识与客观实际相结合；另一方面,还要学习运用想象、联想、演绎、归纳、类比等方法发现客观实际问题，运用分析、综合等方法探索解决问题。在探究性学习的实施过程中教师应把学生作为学习探究和解决问题的主体，并注意转变自己的指导方式。要及时了解学生开展探究活动时遇到的困难以及他们的需要，有针对性地进行指导。教师应成为学生研究信息交汇的枢纽，成为交流的组织者和建议者。在这一过程中要注意观察每一个学生在能力、个性方面的发展，给予适时的指导和帮助。教师切忌将学生探究引向已有的结论，而是提供信息、启发思路、补充知识、介绍方法---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---和线索，引导学生质疑、探究和创新。在现在新课程改革的大背景下,提倡探究性学习更有独特的价值和意义。下面是笔者在一节数学课上和学生不断的进行知识的探究的过程。我们知道有这个结论：在平行四边形ABCD中，对角线的平方和等于四条边的平方和，即：AC2+BD2=2(AB2+AD2)O如果把这个结论放到三角形中，又可以得到:三角形ABC中，AD为BC边上的中线,则有:(2AD)2+BC2=2(AB2+AC2)(以下均记作：结论(*))这个结论可以用向量的基础知识或者余弦定理来证得。在平时的练习中经常遇到有关三角形中线问题，很多情况下可利用这个结论求解。可是这个结论也有它独到之处,有时也有让人意想不到的效果。例(2012苏北四市二模改编呼面上已知点A(dO),B(lQ),直线I:x-y+2=0o试在直线I上求一点P，使得z二PA2+PB2最小。这是一道普通的求距离最值方面的问题。解法一：设P(mzm+2)则有z二PA2+PB2二(m+1)2+(m+2)2+(m-l)2+(m-2)2=4m2+8m+10=4(m+l)2+6所以当m=-l时，z的最小值为6。这本是一个普通的问题，但是经过反思发现，如果利用结论(*),则有独特的解法。---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---图1图2(解法2)由图1,三角形PAB中，P0是AB边上的中线，当P在I上变化时,AB的长度始终不变。由结论(★)可得:(2PO)2+AB2=2(PA2+PB2)---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---当OP丄/时,P0最小。此时P0二10-0+21所以E42+PB2=^-[(2PO)2+AB2]=-y[(2PO)2+4]=4^JIPO2+2这样求z=R42+PB2的最小值就变成了求PO的最小值。---本文来源于网络，仅供参考，勿照抄，如有侵权请联系删除---为定值，则P点的轨迹为以脑中点为心,PA2+PR2的最小值为2X2+2=6利用结论(*)來解题利用了三角形内部的转化，将本身一个代数量的求解转化为求解一个几何量。经过再思考，这种类型的问题还町以进一步进行推广。推广如图2,已知P为圆/+/=4上任意一点,A(-1,0),B(I,0)，求证中中+PB2为定值。证:连接P0,则P0是三角形PAB中3边上的中线。利用结论(*)可得:(2PO)2+AB?=2(R42+W)因为P是圆上任意一点，所以P0=2为定值。而皿二2为定值，故PA'+PF为定值。这个结论反过来也有意义，即4』为2个定点，若PA2+PB?/2E42+2时-4护为半径的圆。推广2：已知P为圆C：(%-l)2+(y-3)2=l上任意一点/(-l,0),B(l,0),求Pf+pF的最小值和最大值。解:连接P。,则P0是三角形PAB中AB边上的中线利用结论(*)可得：｛2PO)2^AB2=2(PA2+PB2)所以要求PA2+PB2的...