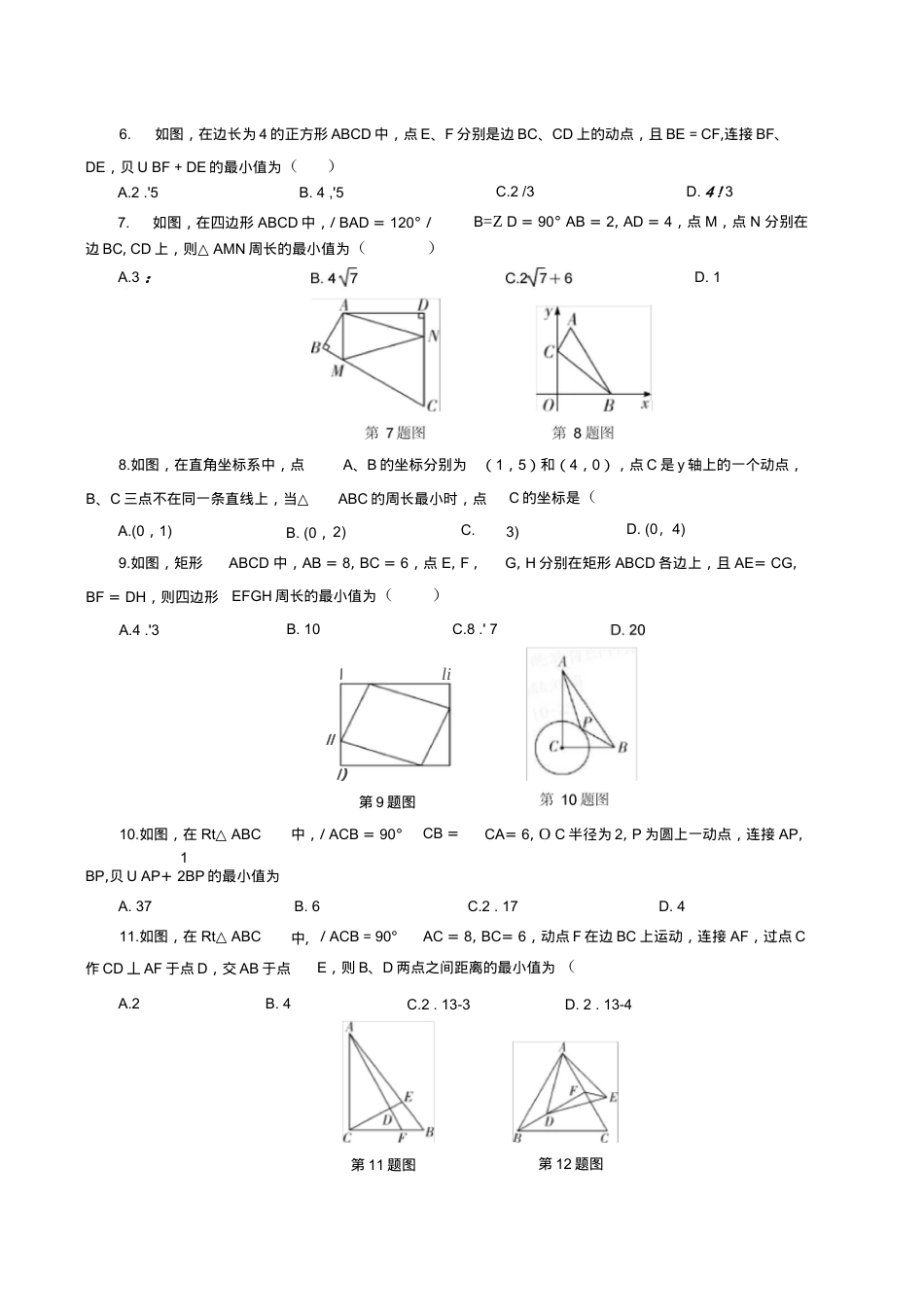
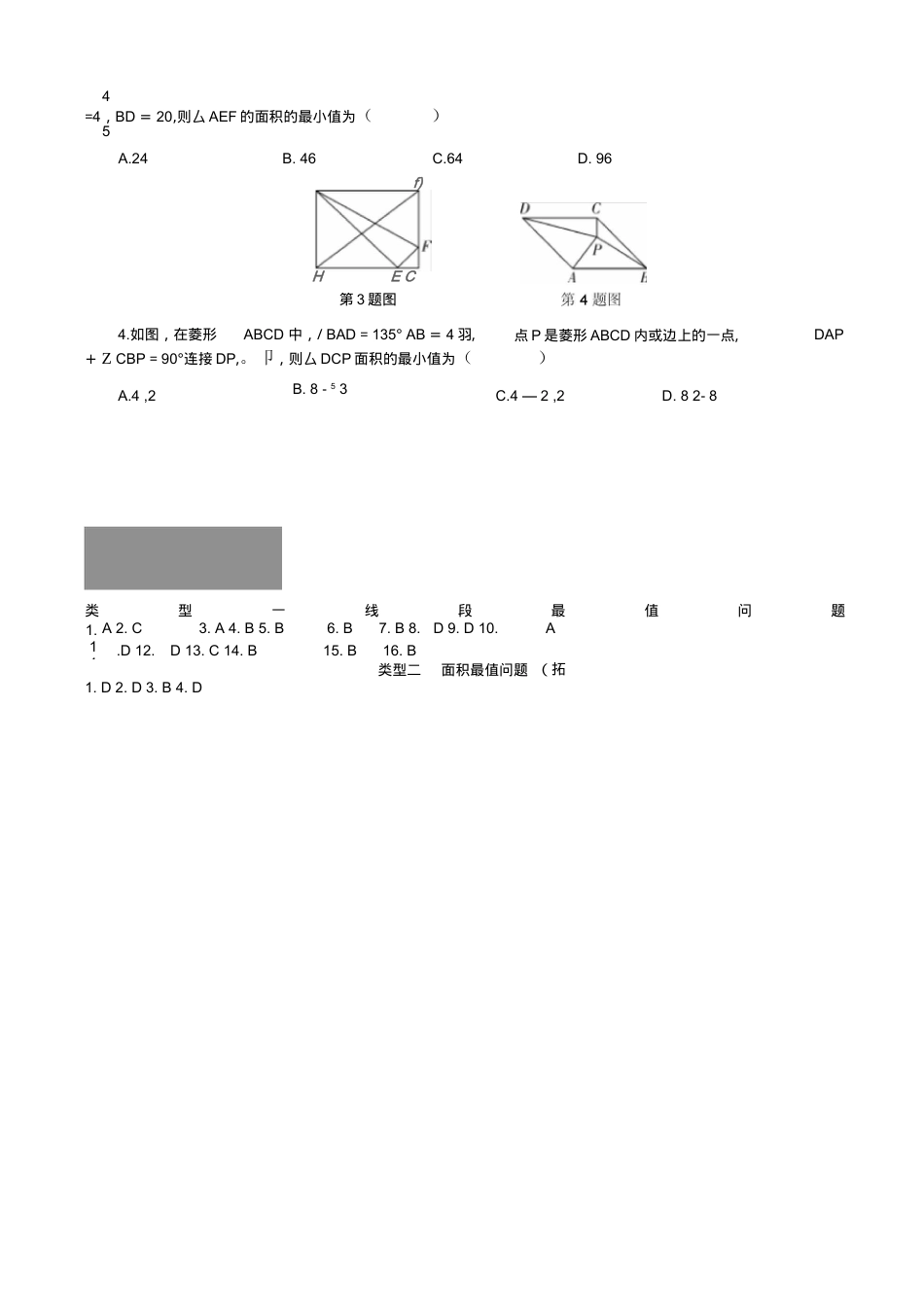
题型二选择压轴题之几何图形最值问题类型一线段最值问题1.如图，在△ABC中，/BAC=90°AB=3,AC=4,P为边BC上一动点，PE丄AB于E,PF丄AC于F,M为EF的中点，贝UPM的最小值为（）和AC上的动点，贝UPC+PQ的最小值是（3.如图，在RtAABC中，/B=90°AB=3,BC=4，点D在BC上，以AC为对角线的所有？ADCE中，DE的最小值是（）点，贝UPC+PD的最小值为（）A.1.2D.2.42.如图，在Rt△ABC中，/ACB=90°12A・5B.424C.24D.5A.3B.2C.4D.54.如图，菱形值是（）ABCD中，/ABC=60°边长为13,P是对角线BD上的一个动点，则2PB+PC的最小C.3D.2+；35.如图，在△ABC中，AC=BC,/ACB=90°点D在BC上，BD=3,DC=1，点P是AB上的动A.4C.1.4AC=6,若P,Q分别是AD第3题图第4题图C.66.如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点，且BE=CF,连接BF、DE，贝UBF+DE的最小值为（）边BC,CD上，则△AMN周长的最小值为（）1BP,贝UAP+2BP的最小值为A.2.'5B.4,'57.如图，在四边形ABCD中，/BAD=120°/C.2/3D.4!3B=ZD=90°AB=2,AD=4，点M，点N分别在A.3：7D.118.如图，在直角坐标系中，点（1，5）和（4，0），点C是y轴上的一个动点，且B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（A.(0，1)B.(0，2)C.(0，3)D.(0，4)9.如图，矩形ABCD中，AB=8,BC=6，点E,F,G,H分别在矩形ABCD各边上，且AE=CG,BF=DH，则四边形A.4.'3EFGH周长的最小值为（）C.8.'7B.10li10.如图，在Rt△ABC中，/ACB=90°CB=4,CA=6,OC半径为2,P为圆上一动点，连接AP,A.37B.6C.2.17D.411.如图，在Rt△ABC中,/ACB=90°AC=8,BC=6，动点F在边BC上运动，连接AF，过点C作CD丄AF于点D，交AB于点E，则B、D两点之间距离的最小值为（A.2B.4C.2.13-3D.2.13-4A、B的坐标分别为\III）第9题图第11题图第12题图接AE、BF，交于点G,连接DG,则DG的最小值为（）16.在RtAABC中，/ACB=90°AC=8,BC=6,点D是以点A为圆心，4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为（）类型二面积最值问题（拓展）1.如图，点E为边长为4的等边△ABC的BC边上一动点（点E不与B、C重合），以AE为边作等边△AEF，则△AEF面积的最小值是（）2.（2017合肥蜀山区模拟）如图，OO的半径是2,直线两个动点，且在直线I的异侧，若/AMB=45°,则四边形MANB面积的最大值是（）3.如图，在矩形ABCD中，AD>AB,点E、F分别是BC、DC上的点，且CE+CF=8，若sin/ABD连接EF，当△AEF周长最小时，/CFE的大小是A.30B.45C.60D.9013.在平面直角坐标系中，点O为坐标原点,占八A、B、C的坐标分别为A（.3,0）、B（3.'3,0）、C（0,5），点D在第一象限内，且/ADB=60°则线段CD的长的最小值是（C.2.'7—2D.2.10—214.如图,在RtAABC中，/C=90°AC=6,BC=8,点F在边AC上，并且CF=2,点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是（A.33C.315.如图,第14题图第15题图正方形ABCD的边长为2,点E、F分别是边BC、CD的延长线上的动点，且CE=DF，连A..;3—1B.,'5—1C.；'3A.8B.7C.6D.5A.2l与OO相交于A、B两点，M、N是OO上的A.2B.4C.2.2D.42第1题图C.34=4，BD=20,则厶AEF的面积的最小值为（）5+ZCBP=90°连接DP,。卩，则厶DCP面积的最小值为（）类型一线段最值问题1.A2.C3.A4.B5.B6.B7.B8.D9.D10.A11.D12.D13.C14.B15.B16.B类型二面积最值问题（拓展）1.D2.D3.B4.DA.4,2B.8-53C.4—2,2D.82-8A.24B.46C.64D.964.如图，在菱形f)HEC第3题图ABCD中，/BAD=135°AB=4羽,点P是菱形ABCD内或边上的一点,DAP