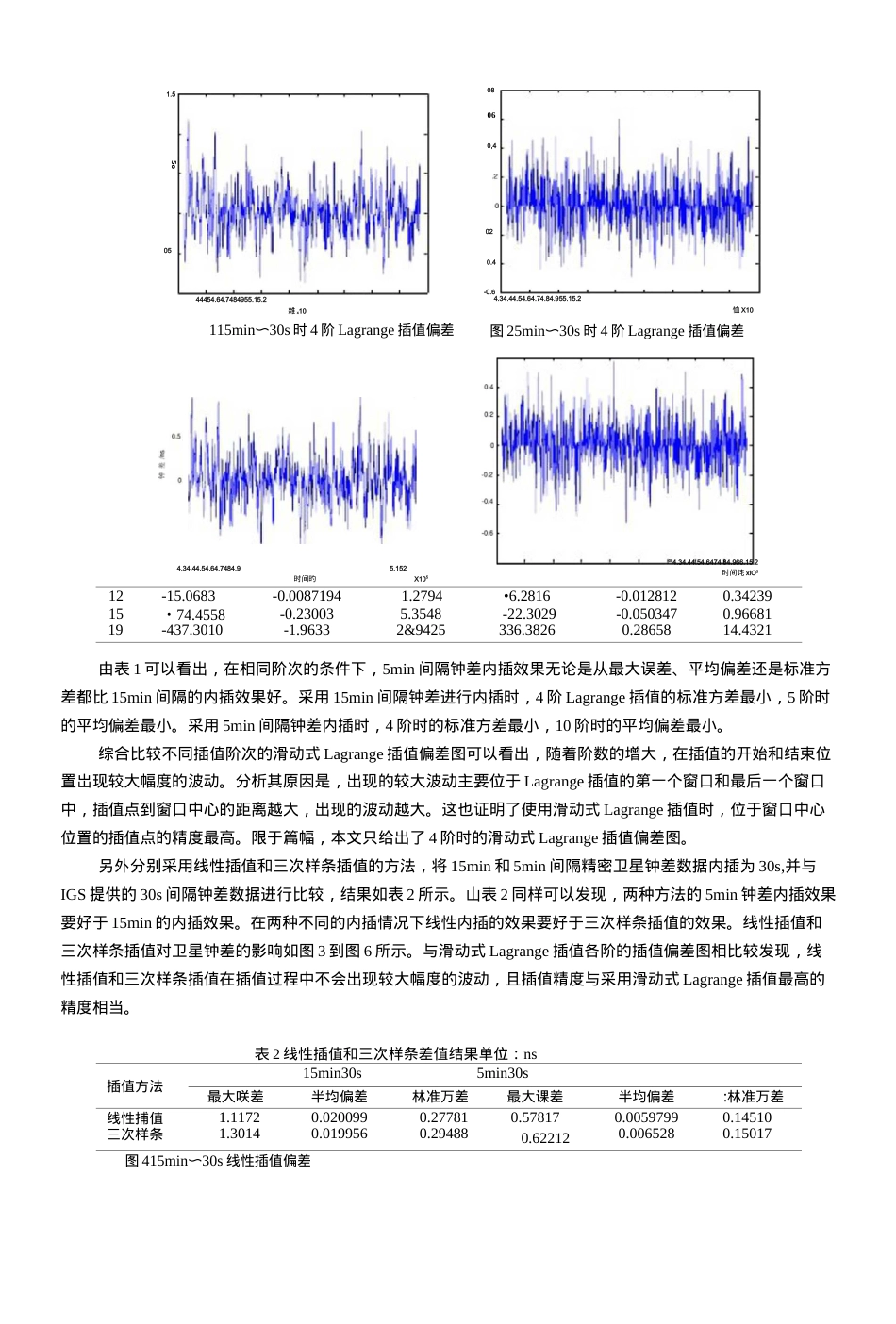
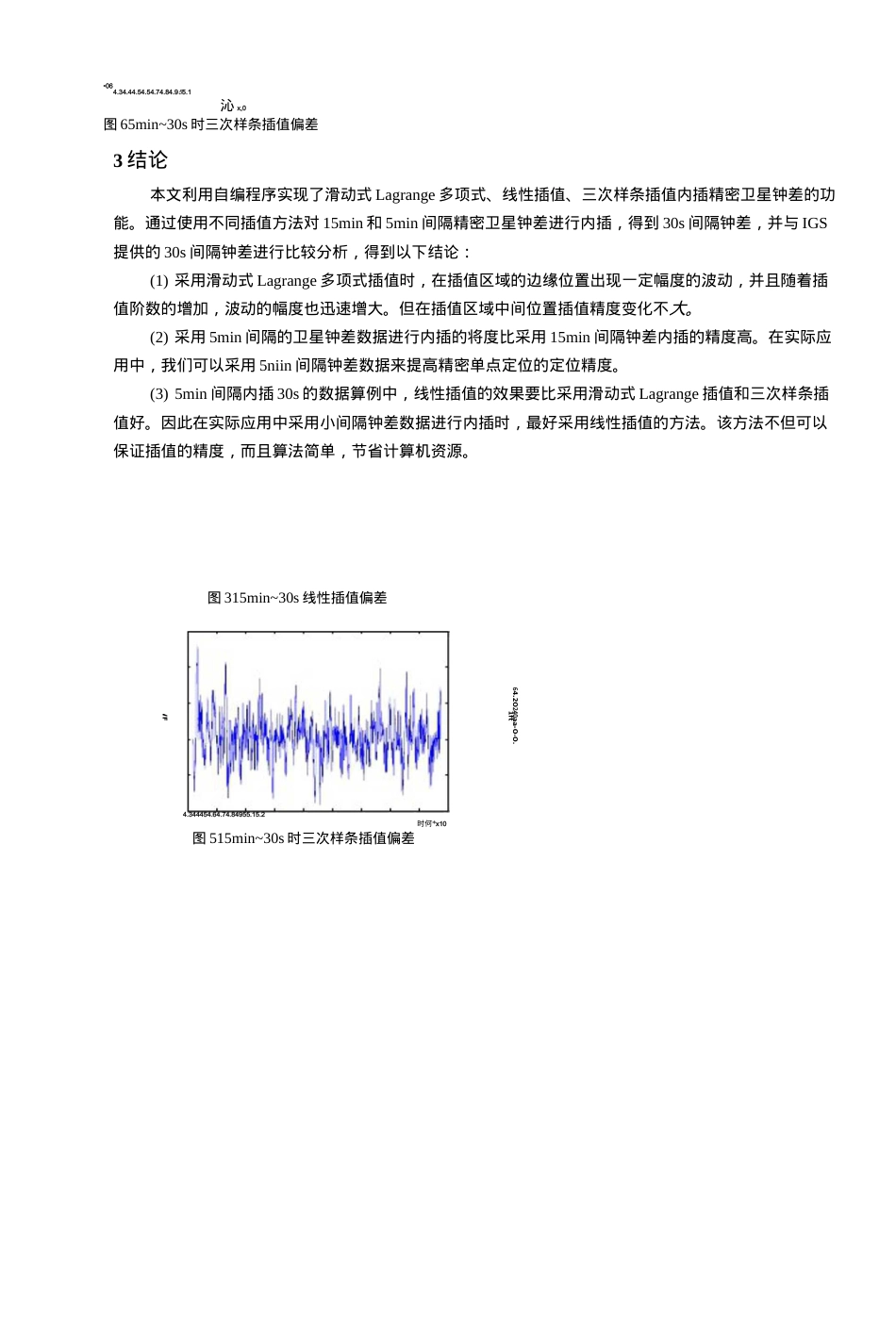
精密卫星钟差内插方法研究李辉，郑南山(中国矿业大学环境与测绘学院，江苏徐州221(X)8)摘要：本文主要介绍了精密单点定位中的精密卫星钟差插值的问题，利用IGS提供的精密卫星钟差，分析和比较利用滑动式拉格朗日插值、线性插值以及三次样条插值三种不同的插值方法，分别通过对15min和5min间隔的卫星钟差进行内插。通过实验分析，取得了一些精密卫星钟差插值的有益结论和建议。关键词：GPS；精密单点定位；卫星钟差；拉格朗日插值中图分类号：P228.4DisscussiononSatelliteClockErrorInterpolationMethodLIHui,ZHENGNanshan(SchoolofEnvironmentScienceandSpatialInformatics,CUMT,JiangsuXuzhou221008)Abstract:ThispaperbrieHyinlroducessatelliteclockbiasinterpolationinprecisepointpositioning,andslidingLagrangeinteipolation,linearinterpolationandcubicsplineinterpolationaretakentostudyonthedensificationofIGSsatelliteclockbiaswith15minand5minintervals.Aftercomparison,theresultsshowthatsatelliteclockbiasinterpolatedfrom5minintervaldatabylinearinterpolationhasgoodperformance・Keywords:GPS,Precisepointpositioning(PPP),Satelliteclockbias,Lagrangeinterpolation0引言GPS精密单点定位技术是近年来GNSS研究领域的一个热点问题。利用精密卫星星历和卫星钟差，以单台双频接收机采集的非差载波相位和伪距数据作为主要观测值来进行单点定位，可以直接得到分米级甚至厘米级的高精度ITRF框架坐标。目前获取的精密卫星钟差数据主要是由IGS提供的15min>5min、或30s采样间隔的卫星钟差,而在实际定位应用中,GPS接收机的采样率一般为30s>15s,甚至更高。要想获得GPS接收机观测历元时刻的卫星钟差，通常可以通过插值的方法实现。目前，国内外常用的插值方法有拉格朗口(Lagrange)插值、线性插值、Newlon插值、Hermile插值以及三次样条差值等本文将利用IGS提供的间隔为15min和5min的精密卫星钟差数据，并采用线性插值、拉格朗日(Lagrange)插值和三次样条插值三种方法进行插值，内插出间隔为30s的卫星钟差数据，以IGS提供的30s间隔钟差数据作为真值，对插值结果进行比较分析，探讨三种方法的插值效果以及不同间隔钟差数据对插值精度的影响。1精密卫星钟差插值算法1.1线性插值线性插值的插值形式为：乙=/0(X)/(Xo)+/i(X)/(Xi)(D作者简介：李辉(1984-)，男，硕士研究生，主要研究方向：IN1U/GPS辅助航空摄影测量通信联系人：郑南山，男，副教授，主要研究方向：卫星定位导航技术及其应用・E・mail:znshcumt@163.com廿亠//XX上..xXXo其中/()(X)=,/1(X)=1(1XiXiXo线性插值的计算过程简单，且易于编程实现。用线性插值的方法可以降低算法的复杂性，提高运算效率。1.2滑动式Lagrange插值算法Lagrange插值函数定义如下：n*0,./i对于n阶插值，即有n+1个己知点，内插位于这n+1个点之间的任意位置的函数值。以IGS提供的精密卫星钟差为基础，使用插值的方法计算岀所需时刻的卫星钟差量，插值中使用的节点数量即为该插值方法的阶。分析Lagrange插值多项式的余项公式可以发现，截断误差在插值端点处易发生跳跃现彖。但滑动式多项式插值方法克服了这一现彖，并可提高插值的精度⑶。为保证最佳的插值效果，保持待求点始终位于插值范围的中心位置。例如五阶Lagrange插值多项式最佳插值时刻为第3和第4个插值节点中间的时刻，即每次取6个数据点，始终保持待求点在第3个和第4个插值节点之间。第一个点到第6个点为第一个插值区间，仅用来插值第3个到第4个之间的时刻。这样的插值区间就相当于一个会移动的窗口，窗口的大小不变，窗口以一定的间隔向后移动，内插出窗口中间位置的精密卫星钟差Mi。在Lagrange插值过程中，多项式的阶数会对插值结果产生影响。如果阶数过低，粘度会达不到粘•密单点定位的婆求；如果阶数过高，不仅会浪费计算机的资源，内插的效果还不一定好⑹。1.3三次样条插值设在区间［a,b］上，给出n+1个互不相同的节点，函数y=/(x)在这些节点上的值为卩*3)(20丄…,町°如果分段表示的函数$(兀)满足以下条件,就称5(X)为三次样条插值函数。1)5(X)在子区间［兀,加］的表达式Si...