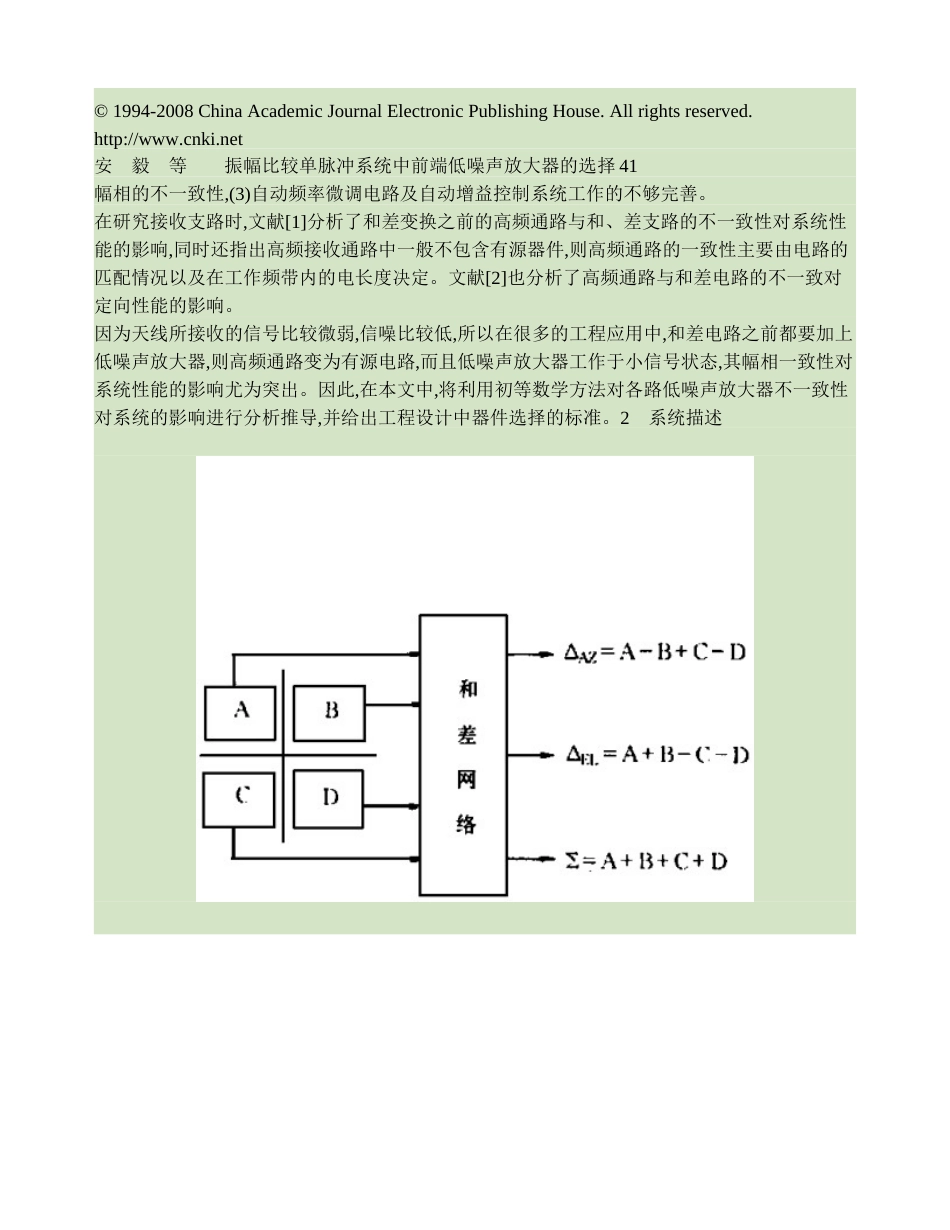
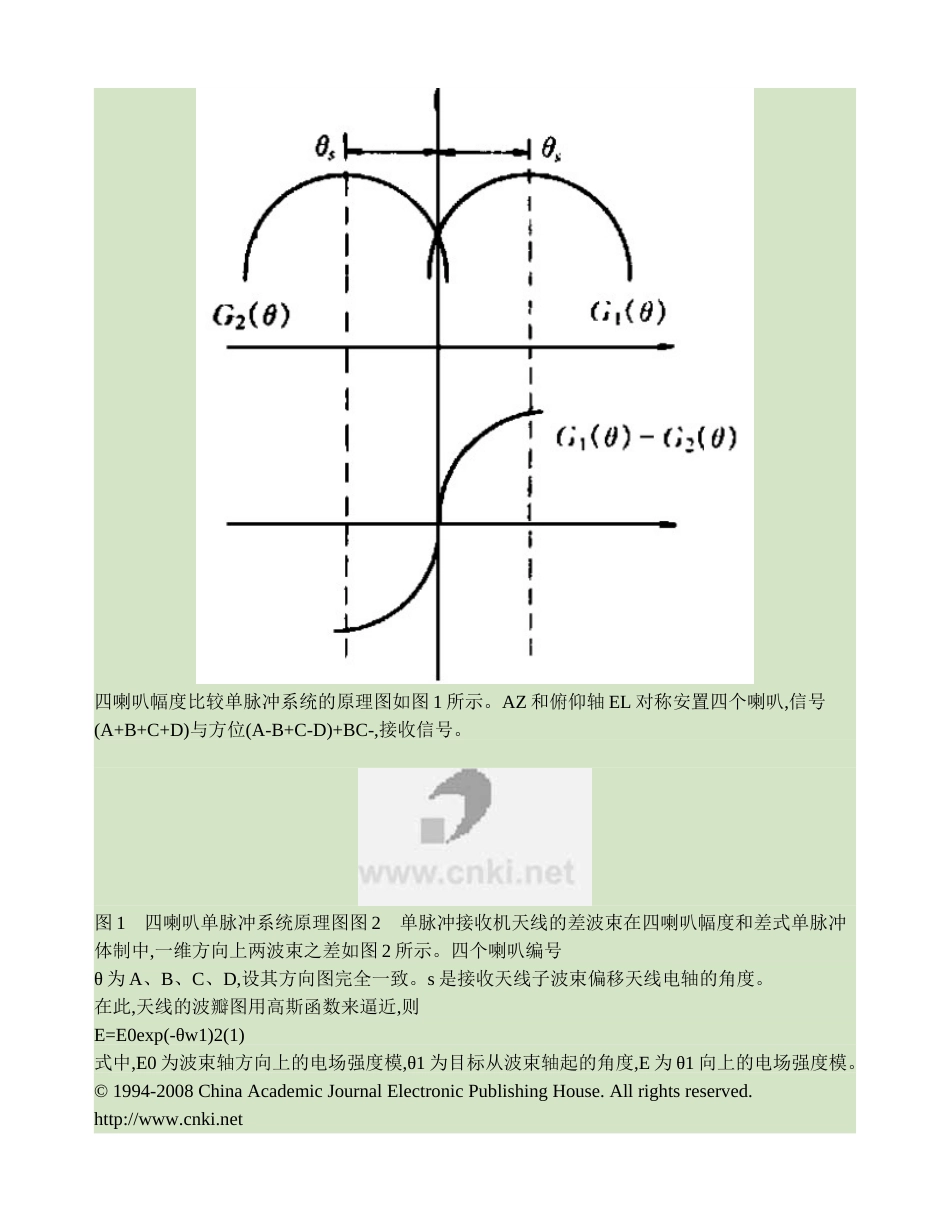
40雷达与对抗2001年第1期振幅比较单脉冲系统中前端低噪声放大器的选择安毅,吕昕,高本庆(北京理工大学电子工程系,北京100081)摘要:针对振幅比较单脉冲体制中前端低噪声放大器特性应保持良好一致性的要求,本文利用数学推导的方法,得出在系统跟踪误差一定时,低噪声放大器之间的电压增益和相移不一致所允许的最大范围,从而给出了低噪声放大器选择的标准,在具体的工程设计中有一定的参考价值。关键词:单脉冲系统;和差电路;低噪声放大器中图分类号:TN85018文献标识码:A()SelectionAmplifiersinMonopulseSystemANYi,LUXin,GAOBen2qing(DepartmentofElectronicEngineering,BeijingInstituteofTechnology,Beijing100081,China)Abstract:Inamplitudecomparisonmonopulsesystem,thefront2endlownoiseamplifiersshouldbeaccordantwell.Inthepaper,themathematicalwayisadoptedtodeducetheunbalancerangeofamplifiers’amplitudegainandphaseshift,accordingtothecertainrangeoftrackingerror.Thatisalsotheselectionstandardoflownoiseamplifiers.Keywords:monopulsesystem;sumanddifferencecircuit;lownoiseamplifier1引言在单脉冲跟踪体制中,利用一个目标回波信号,即可确定目标的位置,是一种先进有效的定向跟踪体制。单脉冲体制的定向精度在很大程度上取决于每对接收支路特性的一致性。在实际情况下,在制造加工方面,或是电路器件选择与装配方面,都可能会出现一些使接收支路特性的一致性受到破坏的缺陷,此时,系统的定向精度会大大地下降。在以往的研究中,对以下一些方面进行了分析:(1)构成天线方向图的缺陷,(2)接收支路收稿日期:2000209214作者简介:安毅(1976-),男,甘肃秦安人,北京理工大学电子工程系博士在读,目前主要从事自适应阵列信号处理系统的研究。©1994-2008ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net安毅等振幅比较单脉冲系统中前端低噪声放大器的选择41幅相的不一致性,(3)自动频率微调电路及自动增益控制系统工作的不够完善。在研究接收支路时,文献[1]分析了和差变换之前的高频通路与和、差支路的不一致性对系统性能的影响,同时还指出高频接收通路中一般不包含有源器件,则高频通路的一致性主要由电路的匹配情况以及在工作频带内的电长度决定。文献[2]也分析了高频通路与和差电路的不一致对定向性能的影响。因为天线所接收的信号比较微弱,信噪比较低,所以在很多的工程应用中,和差电路之前都要加上低噪声放大器,则高频通路变为有源电路,而且低噪声放大器工作于小信号状态,其幅相一致性对系统性能的影响尤为突出。因此,在本文中,将利用初等数学方法对各路低噪声放大器不一致性对系统的影响进行分析推导,并给出工程设计中器件选择的标准。2系统描述四喇叭幅度比较单脉冲系统的原理图如图1所示。AZ和俯仰轴EL对称安置四个喇叭,信号(A+B+C+D)与方位(A-B+C-D)+BC-,接收信号。图1四喇叭单脉冲系统原理图图2单脉冲接收机天线的差波束在四喇叭幅度和差式单脉冲体制中,一维方向上两波束之差如图2所示。四个喇叭编号θ为A、B、C、D,设其方向图完全一致。s是接收天线子波束偏移天线电轴的角度。在此,天线的波瓣图用高斯函数来逼近,则E=E0exp(-θw1)2(1)式中,E0为波束轴方向上的电场强度模,θ1为目标从波束轴起的角度,E为θ1向上的电场强度模。©1994-2008ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net42雷达与对抗2001年第1期w=h2=217738(2θ015)2(2)其中,2θ015为天线子阵列波束的半功率波瓣宽度。假定目标偏离天线方位轴的角度为θ,同时位于俯仰轴上,则四个喇叭天线接收的信号为EA=E0exp[-EC=E0exp[-)2],EB=E0exp[-)2]w(θw(θs-θs+θ22)2],ED=E0exp[-)2]w(θw(θs-θs+θ22(3)设四个低噪声放大器的参数为φAmPA→G∠),m=(1±Δm)AmPB→mG(φ+α∠),n=(1±Δn)AmPC→nG(φ+β∠),h=(1Δh)AmPD→hG(φ+γ(4)∠其中Δmg,-ξΔnΔh,不引入误差。经过和差电路后,可得方位误差信号为=GE0exp[-w(θ)2]cos(wt+φ)-mGE0exp[-)2]w(θs-θs+θ22)+nGE0exp[-)2)]cos(wt+φ+β)cos(wt+φ+αw(θs-θ2)2]cos(wt+φ+γ...